题目:https://odzkskevi.qnssl.com/f85205c68ae5f131a579c799f71b7b69?v=1502173334
旅行商问题描述:平面上n个点,确定一条连接各点的最短闭合旅程。这个解的一般形式为NP的(在多项式时间内可以求出)
J.L. Bentley 建议通过只考虑双调旅程(bitonictour)来简化问题,这种旅程即为从最左点开始,严格地从左到右直至最右点,然后严格地从右到左直至出发点。下图(b)显示了同样的7个点的最短双调路线。在这种情况下,多项式的算法是可能的。事实上,存在确定的最优双调路线的O(n*n)时间的算法。
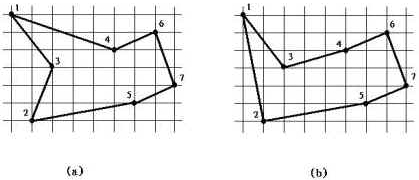
上图中,a是最短闭合路线,这个路线不是双调的。b是最短双调闭合路线。
1.将各点按x从小到大排序
2.定义dp[i][j]为从点i起从右向左走到点1,再从点1从左向右走到点j且经过中途所有点的最短距离,我们默认i一直大于j,dis[i][j]为两点间距离。
3.初始化dp[2][1]=dis[1][2],我们要求的是dp[n][n],而求子问题dp[i][j]可以分成以下三种情况。
(1)j
#include <iostream>
#include <cstring>
#include <stdio.h>
#include <algorithm>
#include <vector>
#include <cmath>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int INF=0x3f3f3f3f;
int n;
double x[1000],y[1000],dis[1000][1000],dp[1000][1000];
double f()
{
dp[2][1]=dis[1][2];
for(int i=3;i<=n;i++)
for(int j=1;j<i;j++)
{
if(j==i-1) //j==i-1时
{
dp[i][j]=INF;
for(int k=1;k<j;k++)
dp[i][j]=min(dp[i][j],dp[j][k]+dis[k][i]);
}
else //j<i-1时
{
dp[i][j]=dp[i-1][j]+dis[i-1][i];
}
}
dp[n][n]=dp[n][n-1]+dis[n-1][n]; //j==i==n时
return dp[n][n];
}
int main()
{
while(cin>>n)
{
for(int i=1;i<=n;i++)
cin>>x[i]>>y[i];
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
dis[i][j]=sqrt((x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]));
printf("%.2f
",f());
}
return 0;
}