goj 百度的面试（单调栈）

Problem Description:

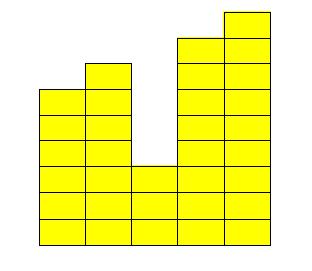
在一个二维平面，从左到右竖立n根高度分别为：a[1],a[2],....a[n]，且宽度都为1的木板。试给出平面内最大的矩阵面积。

Input:

输入包含多组测试数据，每一组数据的第一行输入正整数n(<=5000),下面一行输入序列a[1],a[2],...a[n],其中1<=a[i]<=1000。

Output:

对于每一组测试数据，输出最大的矩形面积。

Sample Input:

5
6 7 3 8 9
3
2 1 4

Sample Output:

16
4
解题思路：题目的意思就是找出最大的矩形面积，思路就是每个当前高度向左向右所能伸长的最大宽度*当前高度，再跟最大值比较即可，数据比较小，水过！
AC代码一：

#include<bits/stdc++.h>
using namespace std;
int a[5005],n,Maxarea,len;
int main()
{
    while(cin>>n){
        for(int i=0;i<n;++i)cin>>a[i];
        Maxarea=0;
        for(int i=0;i<n;++i){
            len=1;
            for(int j=i+1;j<n && a[i]<=a[j];++j)++len;
            for(int j=i-1;j>=0 && a[i]<=a[j];--j)++len;
            Maxarea=max(Maxarea,a[i]*len);
        }
        cout<<Maxarea<<endl;
    }
    return 0;
}

AC代码二：单调栈的运用。时间复杂度是O(n)。

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<string.h>
#include<stack>
using namespace std;
typedef long long LL;
const int maxn=1e5+5;
int n,L[maxn],R[maxn],res,h[maxn];
stack<int> st;
int main(){
    while(~scanf("%d",&n)){
        while(!st.empty())st.pop();memset(L,0,sizeof(L));memset(R,0,sizeof(R));
        for(int i=0;i<n;++i)scanf("%d",&h[i]);
        for(int i=0;i<n;++i){
            while(!st.empty()&&h[st.top()]>=h[i])st.pop();
            L[i]=st.empty()?0:st.top()+1;
            st.push(i);
        }
        while(!st.empty())st.pop();res=0;
        for(int i=n-1;i>=0;--i){
            while(!st.empty()&&h[st.top()]>=h[i])st.pop();
            R[i]=st.empty()?n:st.top();
            st.push(i);
        }
        for(int i=0;i<n;++i)
            res=max(res,h[i]*(R[i]-L[i]));
        cout<<res<<endl;
    }
    return 0;
}