给[L,R]区间的每一个数都质因数分解的复杂度可以达到(R-L)logR,真的涨姿势……
另外,质因数分解有很重要的一点,就是只需要打sqrt(R)以内的素数表就够了……因为超过sqrt(R)的至多只有一个,分解其他的那些剩下的就是了。
果然学习的过程中要精益求精,把时间和空间都尽量降到最低。
此外还有一个很重要的公式。d(i)表示i的因子个数。那么
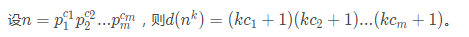
#include<bits/stdc++.h> using namespace std; typedef long long ll; const int MAXN=1000000; int prime[MAXN+1]; void getPrime() { memset(prime,0,sizeof(prime)); for(int i=2; i<=MAXN; i++) { if(!prime[i])prime[++prime[0]]=i; for(int j=1; j<=prime[0]&&prime[j]<=MAXN/i; j++) { prime[prime[j]*i]=1; if(i%prime[j]==0) break; } } } const int md=998244353; long long sj[MAXN+2]; long long fj[MAXN+2]; long long k; void getfact(long long l,long long r) { for (long long i=l;i<=r;i++) { fj[i-l]=1; sj[i-l]=i; } for (int i=1;i<=prime[0];i++) { long long th=prime[i]; for (long long j=(l-1)/th*th+th;j<=r;j+=th) { int cnt=0; while (sj[j-l]%th==0) { cnt++; sj[j-l]/=th; } fj[j-l]=fj[j-l]*(k*cnt%md+1)%md; } } for (long long i=l;i<=r;i++) { if (sj[i-l]!=1) { fj[i-l]=fj[i-l]*(k+1)%md; } } } int main() { getPrime(); int t; scanf("%d",&t); while (t--) { ll l,r; scanf("%I64d%I64d%I64d",&l,&r,&k); getfact(l,r); long long ans=0; for (long long i=l;i<=r;i++) { ans=(ans+fj[i-l])%md; } printf("%I64d ",ans); } return 0; }