二叉树路径问题

1.二叉树的直径

链接：https://leetcode-cn.com/problems/diameter-of-binary-tree/
给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
示例：

输入:  1
     / 
    2   3
   /      
  4   5    
 输出: 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。

递归从下往上，每次获取连接当前结点node和左右子树最长路径，取最大值

var diameterOfBinaryTree = function (root) {
    let max = 0;
    function getMax(node) {
        if (!node) return 0;
        let left = getMax(node.left);
        let right = getMax(node.right);
        /* 连接左右的最大边数 */
        max = Math.max(max, left + right);
        return Math.max(left, right) + 1;
    }
    getMax(root);
    return max;
};

2.二叉树的所有路径

链接：https://leetcode-cn.com/problems/binary-tree-paths/
给定一个二叉树，返回所有从根节点到叶子节点的路径。
说明: 叶子节点是指没有子节点的节点。
示例:

输入:
   1
 /   
2     3
 
  5
输出: ["1->2->5", "1->3"]
解释: 所有根节点到叶子节点的路径为: 1->2->5, 1->3

递归解法
深度优先遍历二叉树并用数组记录经过的结点，到达叶子节点时输出数组内容。

var binaryTreePaths = function (root) {
    let ans = [];
    function dfs(node, arr) {
        if (!node) return;
        arr.push(node.val);//记录结点
        if (!node.left && !node.right) {//叶子结点
            ans.push(arr.join('->'));
            arr.pop();
            return;
        }
        dfs(node.left, arr);
        dfs(node.right, arr);
        arr.pop();//往上回溯，删除当前结点记录
    }
    dfs(root, []);
    return ans;
};

非递归解法
采用后序遍历的解决方案，每次按照左->右->根的顺序遍历，若为叶子节点则将整个栈的值输出。

var binaryTreePaths = function (root) {
    let ans = [], vis = new Set();
    let stack = [], p = root;
    while (stack.length || p) {
        // 往左下找
        while (p) {
            stack.push(p);
            p = p.left;
        }
        let node = stack[stack.length - 1];/* 当前未输出的最左下的结点 */
        if (node.right && !vis.has(node.right)) {/* 右边子树还未遍历 */
            vis.add(node.right);/* 标记防止重复访问 */
            p = node.right;/* 往右子树找 */
        } else {
            if (!node.right && !node.left) /* 叶子节点 */
                ans.push(stack.map(v => v.val).join('->'));
            stack.pop();/* 弹出当前结点，往父节点遍历 */
        }
    }
    return ans;
};

3.二叉树最大路径

链接：https://leetcode-cn.com/problems/binary-tree-maximum-path-sum/
给定一个非空二叉树，返回其最大路径和。
本题中，路径被定义为一条从树中任意节点出发，达到任意节点的序列。该路径至少包含一个节点，且不一定经过根节点。

var maxPathSum = function (root) {
    let max = root.val;
    function getMax(node) {
        /* 空结点返回0 */
        if (!node) return 0;
        /* 最大路径为负值则取0 */
        let left = Math.max(getMax(node.left), 0);
        let right = Math.max(getMax(node.right), 0);
        /* 左右子树最大路径与当前结点连接的权值 */
        let tmp = node.val + left + right;
        max = max > tmp ? max : tmp;
        /* 选择左右路径大的一边连接 */
        return Math.max(left, right) + node.val;
    }
    getMax(root);
    return max;
}
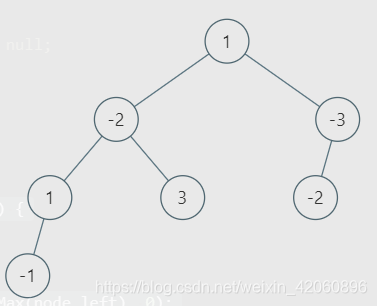
let root = {
    val: 1,
    left: {
        val: -2,
        left: {val: 1,left: {val: -1}
        },
        right: {al: 3}
    },
    right: {
        val: -3,
        left: {val: -2}
    }
}
console.log(maxPathSum(root));//3