软件设计师06-算法

算法特性

有穷性、确定性、有>=0的输入、有>=1的输出、有效性

 算法的复杂度

log2n推导

log2n复杂度一般为树

一棵三层的排序二叉树。节点数为7，查询某个数最多比对3次（和层次一样）

节点数和层次（也是比对的次数）的关系    2^3-1=7，忽略1，得出公式log2 7=3

即

比对次数 = log2n

n即为节点数。

查找

顺序查找

逐个比对，直到找到为止。

二分查找

前提是要有序排列，详细

二分查找（折半查找）在查找成功时关键字的比较次数最多为log2n + 1

时间复杂度为O(log2n)

散列表

散列表（Hash table，也叫哈希表），是根据关键码值(Key value)而直接进行访问的数据结构。也就是说，它通过把关键码值映射到表中一个位置来访问记录，以加快查找的速度。这个映射函数叫做散列函数，存放记录的数组叫做散列表。

给定表M，存在函数f(key)，对任意给定的关键字值key，代入函数后若能得到包含该关键字的记录在表中的地址，则称表M为哈希(Hash）表，函数f(key)为哈希(Hash) 函数。

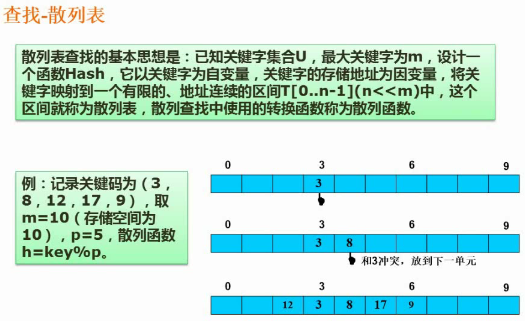
解决散列表冲突

线性探测法

线性探测是一个用来解决冲突的策略，其将新键丢进最靠近的下一个未存数据的单元中。

key1：hash(key)+0

key2：hash(key)+1

key3：hash(key)+2

。。。

二次探测法

hi=(h(key)+i*i)%m   （0<i<m-1）

伪随机数法

排序

概念

稳定排序与不稳定排序

假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些相同关键字的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。

排序的内容是一个复杂对象的多个数字属性，且其原本的初始顺序存在意义，那么我们需要在二次排序的基础上保持原有排序的意义，才需要使用到稳定性的算法，例如要排序的内容是一组原本按照价格高低排序的对象，如今需要按照销量高低排序，使用稳定性算法，可以使得想同销量的对象依旧保持着价格高低的排序展现，只有销量不同的才会重新排序。（当然，如果需求不需要保持初始的排序意义，那么使用稳定性算法依旧将毫无意义）。

稳定算法：冒泡排序、插入排序、归并排序、基数排序
不稳定算法 ：选择排序、快速排序、希尔排序、堆排序

内排序与外排序

内部排序是指待排序列完全存放在内存中所进行的排序过程，适合不太大的元素序列。（下面的排序都是内部排序）

外部排序指的是大文件的排序，即待排序的记录存储在外存储器上，待排序的文件无法一次装入内存，需要在内存和外部存储器之间进行多次数据交换，以达到排序整个文件的目的。

排序方法分类

直接插入排序

插入类的一种，稳定排序，时间复杂度：O(n^2)，空间复杂度：O(1)。

当数据量比较小或者基本有序时效率非常高（希尔排序弥补了无序效率低下的问题）。

    /**
     * 插入排序 - 简单插入排序
     * 稳定排序(如果不小于就不挪动) 时间:O(n^2) 空间:O(1)
     * @param arr 待排序数组
     */
    private static int[] insertSort(int[] arr) {
        /* 首先排除待排序数组为null或者长度为1的 */
        if (arr == null || arr.length < 2) {
            return arr;
        }
        // 从下标1开始遍历(留第一位用于比较)
        for (int i = 1; i < arr.length; i++) {
            int temp = arr[i];  // 待插入的数据,存入temp
            int indx = i;   // 待插入位置的下标index,存入index

            for (int j = i - 1; j >= 0; j--) { //遍历已排序好的序列(共i-1位)
                if (arr[j] > temp) { // 直接和待排序数据对比,如果待排序序列小于arr[j]
                    arr[j + 1] = arr[j]; // 将数据赋给后一位(第一次的j+1就是待排序的位置)
                    indx = j; // 记录当前index
                } else { // 当序列找到位置时
                    break; // 直接跳出,不做无用功
                }
            }
            arr[indx] = temp; // 将待插入的值放入index下标中
        }
        return arr;
    }

希尔排序

本质是分组插入，当数据大时，希尔排序的效率比较高。

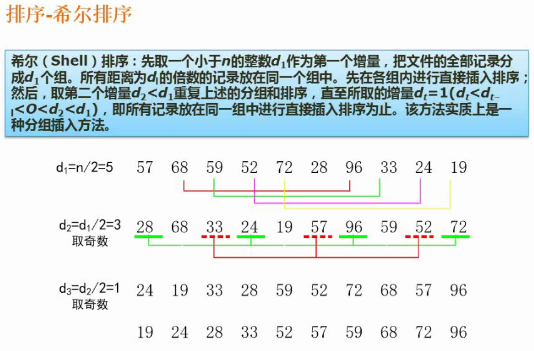
上图中n为序列长度，其中19若是简单插入排序，则在最后插入时要比较多次，若使用希尔排序，则在开始一轮就会调到前面去。

    /**
     * 插入排序 - 希尔排序
     * 不稳定排序 时间:O(n^1.3 ~ n^2) 空间:O(1)
     * @param arr 待排序数组
     */
    public static void shellSort(int[] arr){
        int len = arr.length;
        //进行分组,最开始的增量gap为数组长度的一半
        for (int gap = len/2; gap >0; gap/=2) {
            //对各个分组进行插入排序
            for (int i = gap; i < len; i++) {  //i为每组第二个元素开始,例如len=8,gap=2时,i为2,3,4,5,6,7.这些下标会和自己所属组的前部分进行插入排序
                //将arr[i]插入到所在分组的正确位置上
                insert(arr, gap, i);
            }
        }
    }
    
    /**
     * 希尔排序组内插入排序 - 待插入排序和前面部分(同组)的进行比较插入
     * @param arr 待排序数组
     * @param gap 间隔
     * @param i 待插入下标
     */
    private static void insert(int[] arr,int gap,int i){
        int inserted = arr[i]; //取出待插入数据元素
        int index = i; //待插入下标 
        int j;
        for (j = i-gap; j>=0 && inserted < arr[j]; j-=gap) {  //循环内只有一个if可以直接卸载for的判断条件里
            arr[j+gap] = arr[j];  //把前一个后移一位
            index = j;  //空出来的下标为待插入位置
        }
        arr[index] = inserted;    
    }

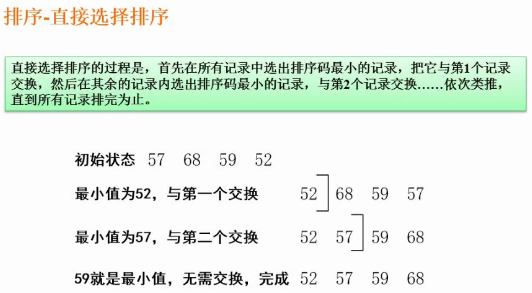
直接选择排序

第一轮把最小的放在第一位，第二轮把第二小的放在第二位，以此类推。

    /**
     * 选择排序 - 简单选择排序
     * @param arr 待排序数组
     */
    public static void selectSort(int[] arr) {   
        if((arr == null) || (arr.length == 0))    
            return ;   
        for(int i = 0; i < arr.length-1; i ++){      
            int minIndex = i; //无序部分的最小数据数组下标    
            for(int j = i + 1;j < arr.length;j ++){
                // 在无序区中找到最小数据并保存其数组下标  
                if(arr[j] < arr[minIndex]){
                    minIndex = j;
                }
            }
            // 将最小元素放到本次循环的前端
            int temp = arr[i];
            arr[i] = arr[minIndex];
            arr[minIndex] = temp;
        }
    }

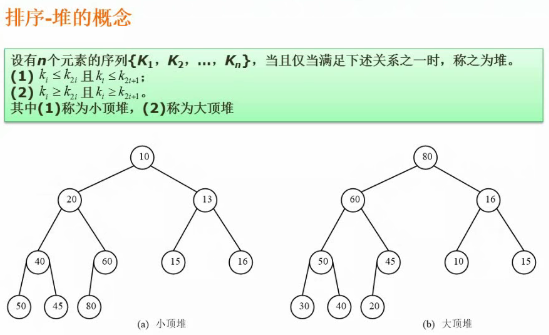
堆排序

堆是一个完全二叉树，当所有结点都小于左右子结点即为小顶堆。当所有结点都大于左右子结点即为大顶堆。

排序的思想是取出堆顶->重组堆->再取出堆顶->再重组堆。

    /**
     * 选择类 - 堆排序
     * 不稳定排序 时间:O(nlog2n) 空间:O(1)
     * @param array 待排序数组
     */
    public static void heapSort(int[] arr){
        /*从右到左从下至上每个子树逐步建立最大堆*/
        for (int i = arr.length/2-1; i >= 0; i--) {   //从最后一个非叶子结点(array.length/2 - 1)遍历到根结点
            ajustHeap(arr,i,arr.length); //调整堆,i决定调整的哪个子树
        }
        /*建立最大堆结束,下面开始排序逻辑*/
        //把大顶堆的根元素，放到数组的最后；换句话说，就是每一次的堆调整之后，都会有一个元素到达自己的最终位置
        for (int i = arr.length-1; i >0 ; i--) {  //这里是遍历堆的长度
            swap(arr, 0, i);  //将已排序好的最大堆第一位和最后一位交换位置
            //再重建最大堆
            ajustHeap(arr, 0, i);  //这里其实只要排序第一个元素到指定位置,又会自动把最大值放在堆顶
        }
    }
    
    /**
     * 建立最大堆，这里是堆顶调整到正确的位置（仅仅是堆顶一直向下这一轮）
     * @param arr 待排序数组
     * @param rootIndex 起始结点
     * @param len 堆的长度
     */
    public static void ajustHeap(int[] arr,int rootIndex,int len){
        //2*rootIndex+1为rootIndex的左子树(因为i是从0开始的),2*k+1为k的左子树
        for (int i = 2*rootIndex+1; i < len; i=2*i+1) {  //遍历树的左节点,root根结点->左子节点->左子结点
            
            if (i+1<len && arr[i+1] > arr[i]) {  //如果有右子树,并且右子树大于左子树
                i++;  //让i先指向子节点中最大的节点,同时这一步决定了下一个遍历的是左子树还是右子树
            }
            
            if (arr[rootIndex]<arr[i]) {  //如果根结点小于子结点(左右子结点)，则进行值的交换
                swap(arr,rootIndex,i);  //根结点和子结点交换
                rootIndex = i;  //根结点更新
            }else{  //此节点大于左右子树,不用交换,直接终止循环
                break;
            }
        }
    }
    
    public static void swap(int[] arr,int a,int b){
        int temp = arr[a];
        arr[a] = arr[b];
        arr[b] = temp;
    }

冒泡排序

    /**
      * 交换排序 - 冒泡排序
      * 稳定排序 时间:O(n^2) 空间:O(1)
      */
    public static void bubbleSort(int[] arr){
        for (int i = 0; i < arr.length-1; i++) {  //遍历循环的圈数(每一次都会有一个最大值放冒泡到后面)
            for (int j = 0; j < arr.length-1-i; j++) {  //这里遍历的范围为length-1-i,预留一位用于+1和后一位比较,每次都会有最大值到末位
                if (arr[j]>arr[j+1]) {
                    swap(arr, j, j+1);
                }
            }
        }
    }
    public static void swap(int[] arr,int a,int b){
        int temp = arr[a];
        arr[a] = arr[b];
        arr[b] = temp;
    }

快速排序

用到了分治法，是一个比较高效的排序。但是因为分治法用到了递归，每次递归都要保持一些数据，所以时间复杂度比一般的要高。

    /**
     * 选择排序 - 快速排序
     * 不稳定排序 时间:O(nlog2n~n^2) 空间:O(log2n)
     * @param arr 数组
     * @param low 最低位
     * @param high 最高位
     */
    private static int[] quickSort(int[] arr, int low, int high) {
        if (low < high) {
            //找寻基准数据的正确索引
            int index = getIndex(arr, low, high);
            //进行迭代对index之前和之后的数组进行相同的操作使整个数组变成有序
            quickSort(arr, low, index - 1);
            quickSort(arr, index + 1, high);
        }
        return arr;
    }
    
    /**
     * 返回基准值的下标
     */
    private static int getIndex(int[] arr, int low, int high) {
        // 把基准数据存入到temp中
        int tmp = arr[low];
        while (low < high) {
            // 当队尾的元素大于等于基准数据时,向前挪动high指针
            while (low < high && arr[high] >= tmp) {
                high--;
            }
            //如果队尾元素小于tmp了,需要将其赋值给low
            arr[low] = arr[high];
            
            //当队首元素小于等于tmp时,向前挪动low指针
            while (low < high && arr[low] <= tmp) {
                low++;
            }
            //当队首元素大于tmp时,需要将其赋值给high
            arr[high] = arr[low];
        }
        // 跳出循环时low和high相等,此时的low或high就是tmp的正确索引位置
        // 由原理部分可以很清楚的知道low位置的值并不是tmp,所以需要将tmp赋值给arr[low]
        arr[low] = tmp;
        return low; // 返回tmp的正确位置
    }

调用

public static void main(String[] args) throws InterruptedException {
    int[] arr = new int[] { 5, 3, 7, 13, 52, 127, 4};
    quickSort(arr,0,arr.length-1);    //最高位一定要写length-1
    System.out.println(Arrays.toString(arr));    
}

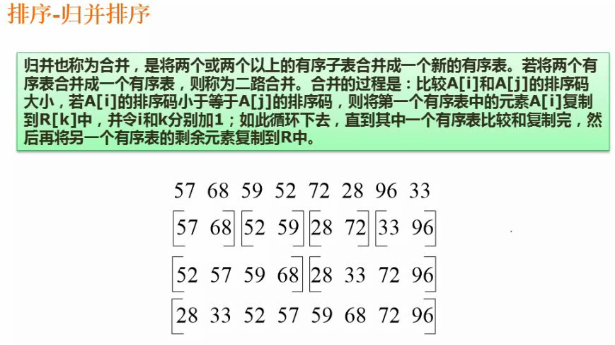
归并排序

采用分治法，但是会递归创建小的数组。空间复杂度比快速排序高一些。

    /**
     * 归并排序
     * 稳定排序 时间:O(nlog2n) 空间:O(n)
     * @param arr 数组
     * @param low 最低位
     * @param high 最高位
     * @return 返回新的数组
     * @return
     */
    public static int[] mergeSort(int[] arr, int low, int high) {
        if (low == high)  //出口
            return new int[] { arr[low] };
         
        int mid = low + (high - low) / 2;
        int[] leftArr = mergeSort(arr, low, mid);    //递归左有序数组,返回的数组时排序好的
        int[] rightArr = mergeSort(arr, mid + 1, high);    //递归右有序数组,返回的数组时排序好的
        int[] newNum = new int[leftArr.length + rightArr.length];    //新有序数组
         
        int m = 0, l = 0, r = 0;    //m是新数组目前下标,l是左数组下标,r是右数组下标
        /**
         * 将左右有序数组按大小赋值到新数组中,直到其中一个数组结束(此时另一个数组剩下的部分一定比已排序数组最后一个大)
         */
        while (l < leftArr.length && r < rightArr.length) {  
            newNum[m++] = leftArr[l] < rightArr[r] ? leftArr[l++] : rightArr[r++];  //比较两个数组中哪个值小并赋给新数组
        }
        
        //只需要把另一个数组剩下的部分直接赋给新数组即可,下面这两个while只会执行一个
        while (l < leftArr.length)
            newNum[m++] = leftArr[l++];
        while (r < rightArr.length)
            newNum[m++] = rightArr[r++];
        return newNum;
    }

调用

    public static void main(String[] args) {
        int[] result = mergeSort(arr, 0, arr.length - 1);
        System.out.println(Arrays.toString(result));
    }

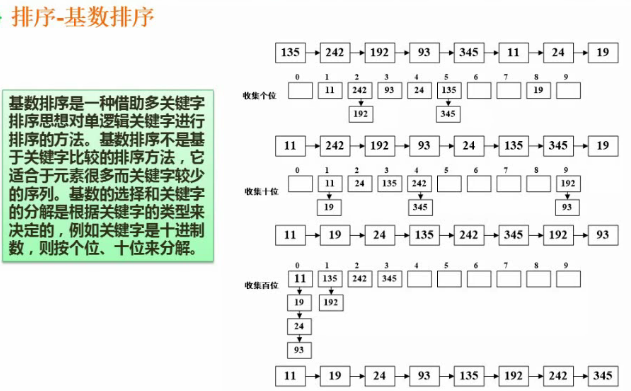
基数排序

    /**
     * 基数排序
     * @param arr 待排序数组
     * @param d 表示最大的数有多少位
     */
    public static void radixSort(int[] arr, int d)
    {
        int k = 0;
        int n = 1;
        int m = 1; //控制键值排序依据在哪一位
        int[][] temp = new int[10][arr.length];  //数组的第一维表示可能的余数0-9
        int[] order = new int[10];  //数组orderp[i]用来表示该位是i的数的个数
        while (m <= d) {
            for (int i = 0; i < arr.length; i++) {
                int lsd = ((arr[i] / n) % 10);
                temp[lsd][order[lsd]] = arr[i];
                order[lsd]++;
            }
            for (int i = 0; i < 10; i++) {
                if (order[i] != 0)
                    for (int j = 0; j < order[i]; j++) {
                        arr[k] = temp[i][j];
                        k++;
                    }
                order[i] = 0;
            }
            n *= 10;
            k = 0;
            m++;
        }
    }

排序复杂度比较

用到分治法的排序算法：快速排序、归并排序

时间复杂度解析：用到分治法的时间复杂度都为nlog2n，用到堆（树）的时间复杂度也是nlog2n。

快速排序为什么是nlog2n的原因：

快速排序使用的空间是O(1)的，也就是个常数级；而真正消耗空间的就是递归调用（分治法用到递归）了，因为每次递归就要保持一些数据；

code

参考：

https://blog.csdn.net/u013384984/article/details/79496052