洛谷P1364 医院设置（Floyd）

题目描述

设有一棵二叉树，如图：

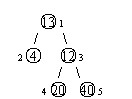
其中，圈中的数字表示结点中居民的人口。圈边上数字表示结点编号，现在要求在某个结点上建立一个医院，使所有居民所走的路程之和为最小，同时约定，相邻接点之间的距离为l。如上图中，

若医院建在1 处，则距离和=4+12+2*20+2*40=136；若医院建在3 处，则距离和=4*2+13+20+40=81……

输入输出格式

输入格式：

第一行一个整数n，表示树的结点数。(n≤100)

接下来的n行每行描述了一个结点的状况，包含三个整数，整数之间用空格(一个或多个)分隔，其中：第一个数为居民人口数；第二个数为左链接，为0表示无链接；第三个数为右链接。

输出格式：

一个整数，表示最小距离和。

输入输出样例

输入样例#1：

5						
13 2 3
4 0 0
12 4 5
20 0 0
40 0 0

输出样例#1：

81

本来是想刷一下树形结构的题目，结果这题赤裸裸Floyd啊！计算 出两点间最小距离，然后枚举医院的设置点，取最小就行了。

代码如下：

#include <bits/stdc++.h>

using namespace std;
#define inf 0x3f3f3f3f
int hspt[110][110],num[110],n,x,y;
int main()
{
    //freopen("de.txt","r",stdin);
    scanf("%d",&n);
    int ans=inf;
    memset(hspt,inf,sizeof hspt);
    for (int i=1;i<=n;++i)
    {
        scanf("%d%d%d",&num[i],&x,&y);
        hspt[x][i]=1;
        hspt[i][x]=1;
        hspt[y][i]=1;
        hspt[i][y]=1;
    }
    for (int k=1;k<=n;++k)//Floyd算法
        for (int i=1;i<=n;++i)
            for (int j=1;j<=n;++j)
            if (i!=j&&j!=k)
            hspt[i][j]=min(hspt[i][j],hspt[i][k]+hspt[k][j]);
    for(int i=1;i<=n;++i)
    {
        int tot=0;
        for (int j=1;j<=n;++j)
        {
            if (i!=j)
            tot+=hspt[i][j]*num[j];
        }
        ans=min(ans,tot);
    }
    printf("%d
",ans);
    return 0;
}