原创转载请注明出处：https://www.cnblogs.com/agilestyle/p/12777788.html
SVM
SVM 作为有监督的学习模型，通常可以进行模式识别、分类以及回归分析。
- SVM 实际上适用于任何维度，在不同维度下， SVM 寻找类似二维直线的东西
- 在三维情形下， SVM 寻找一个 平面（plane）
- 在更高维度下， SVM 寻找一个 超平面（hyperplane） 这也正是支持向量得名的由来。在高维下，数据点是多维向量，间隔的边界也是超平面。支持向量位于间隔的边缘，“支撑”起间隔边界超平面。
- 可以被一条直线（更一般的，一个超平面）分割的数据称为线性可分（linearly separable）数据。超平面起到线性分类器（linear classifier）的作用。
概念引入
桌子上放了红色和蓝色两种球，用一根棍子将这两种颜色的球分开
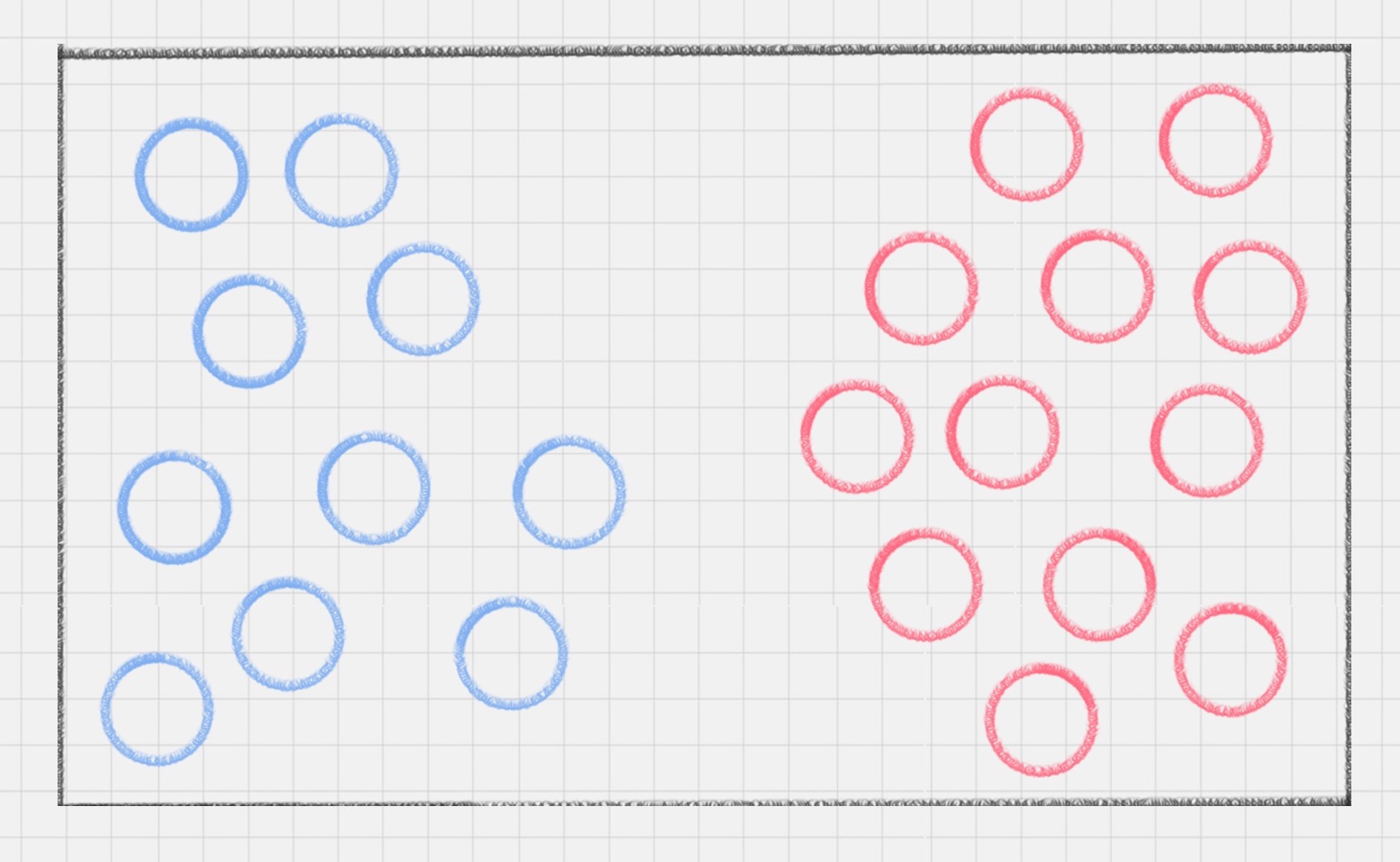
可以很快想到解决方案，在红色和蓝色球之间画条直线
这次难度升级，桌子上依然放着红色、蓝色两种球，但是它们的摆放不规律。如何用一根棍子把这两种颜色分开
一根棍子是分不开的。除非把棍子弯曲
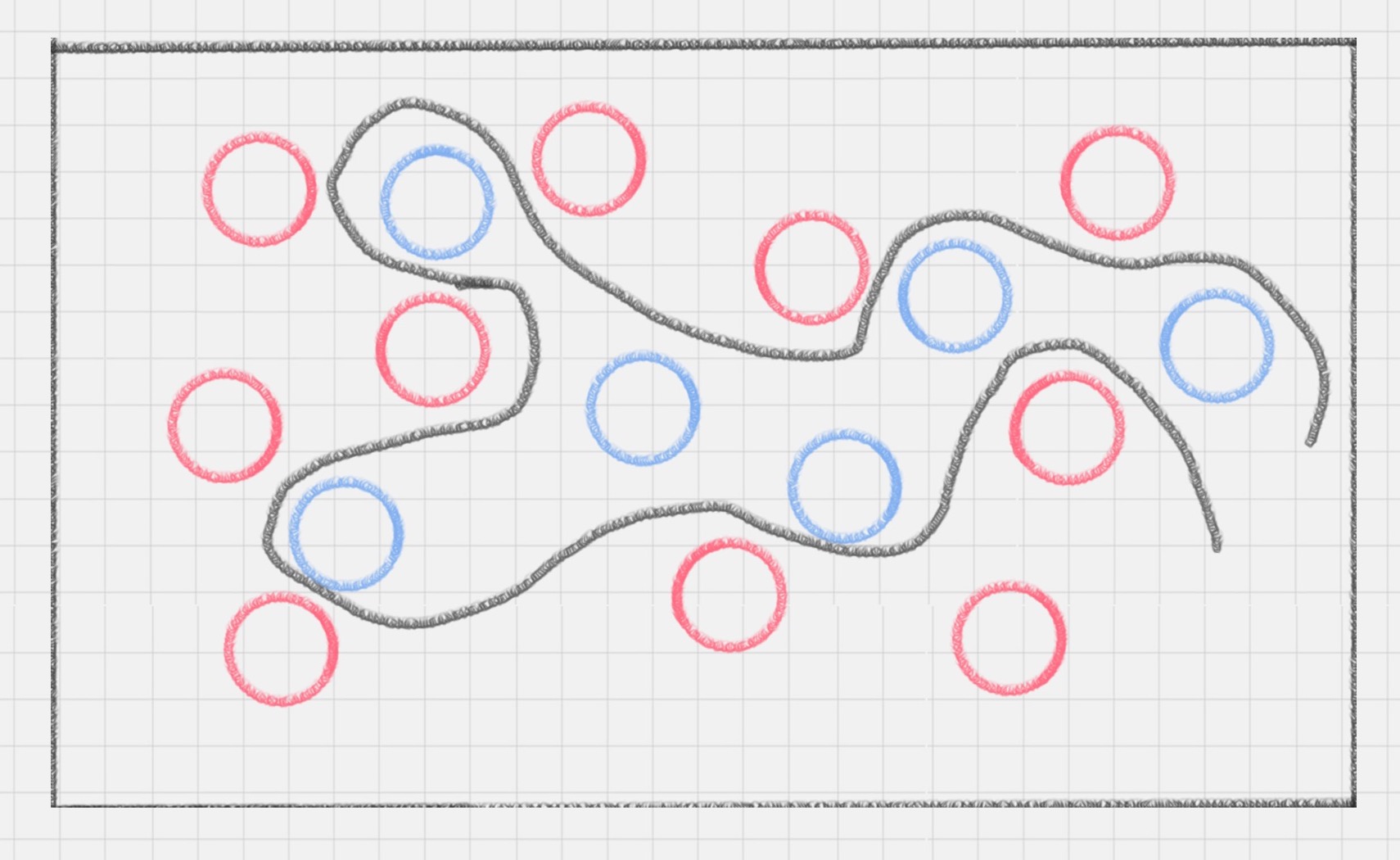
所以这里直线变成了曲线。如果在同一个平面上来看，红蓝两种颜色的球是很难分开的
猛拍一下桌子，这些小球瞬间腾空而起。在腾起的那一刹那，出现了一个水平切面，恰好把红、蓝两种颜色的球分开。
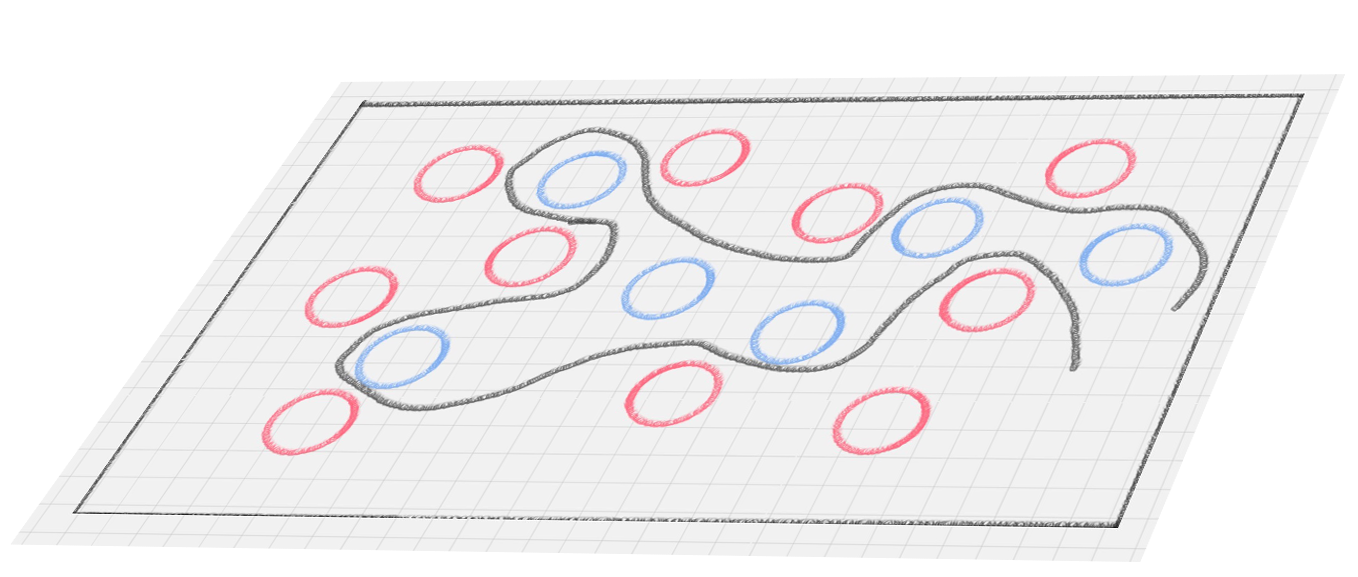在这里，二维平面变成了三维空间。原来的曲线变成了一个平面。
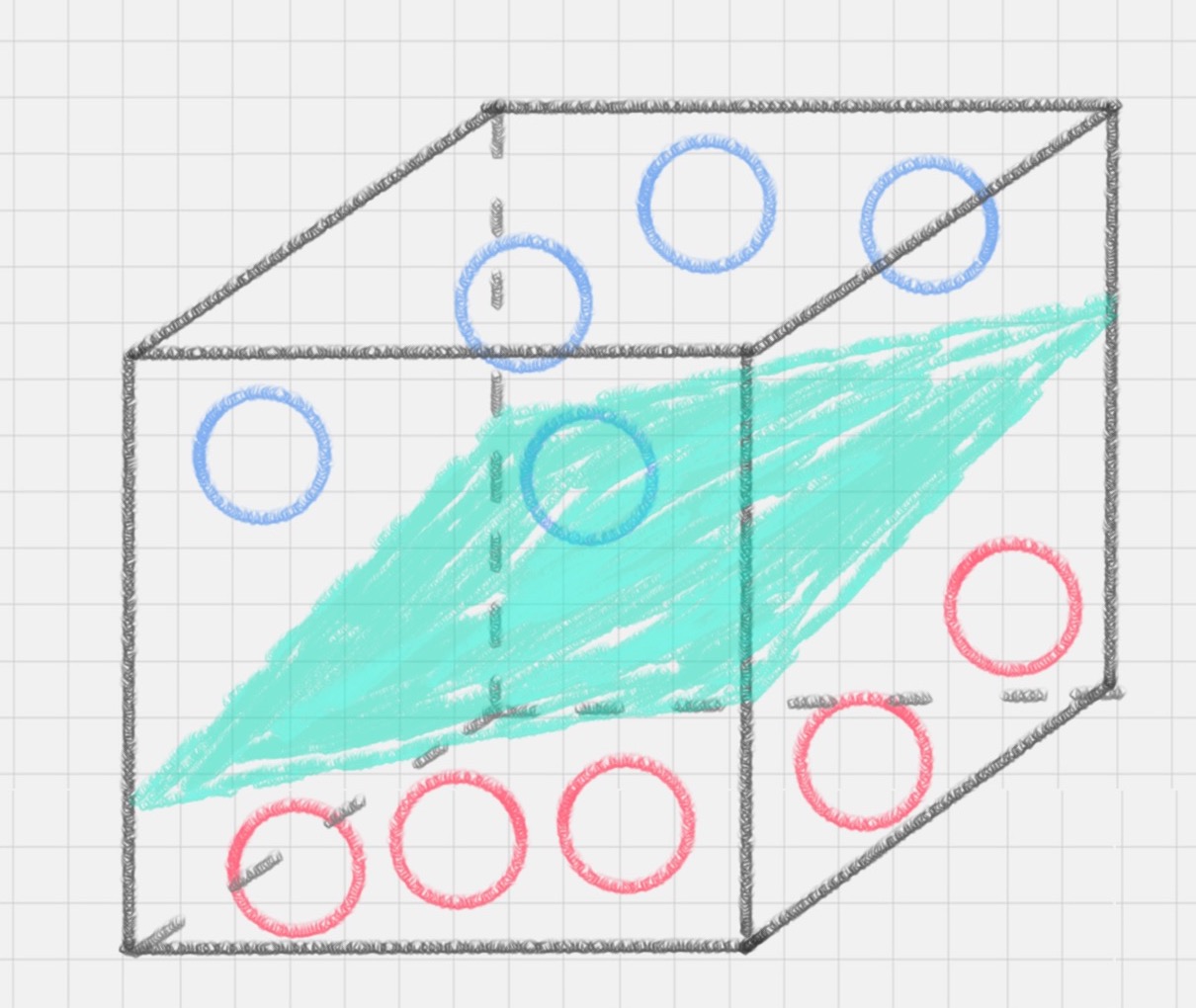
SVM 的工作原理
用 SVM 计算的过程就是帮找到那个超平面的过程，这个超平面就是 SVM 分类器。
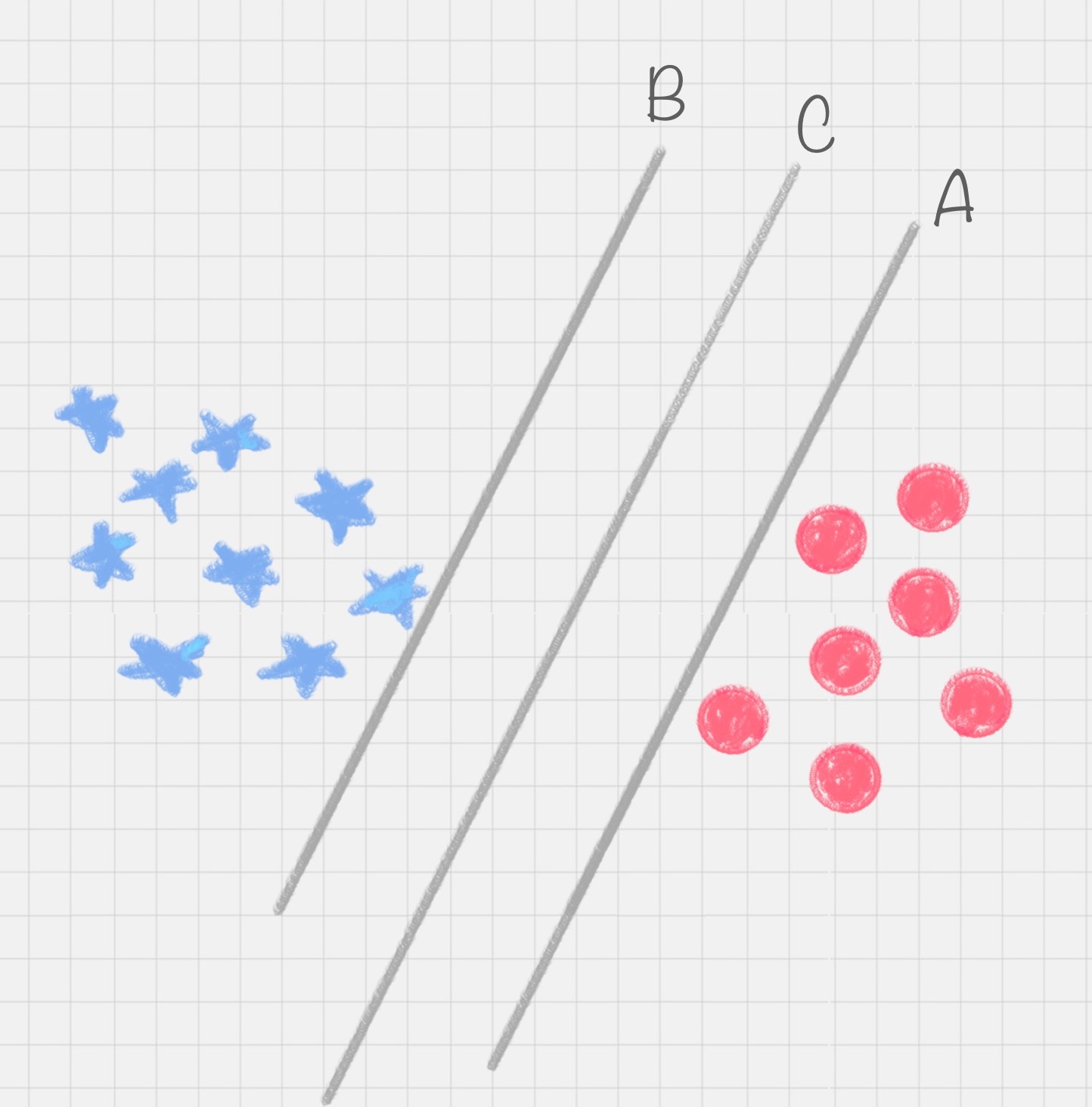
很明显图中的直线 B 更靠近蓝色球，但是在真实环境下，球再多一些的话，蓝色球可能就被划分到了直线 B 的右侧，被认为是红色球。同样直线 A 更靠近红色球，在真实环境下，如果红色球再多一些，也可能会被误认为是蓝色球。所以相比于直线 A 和直线 B，直线 C 的划分更优，因为它的鲁棒性更强。
分类间隔
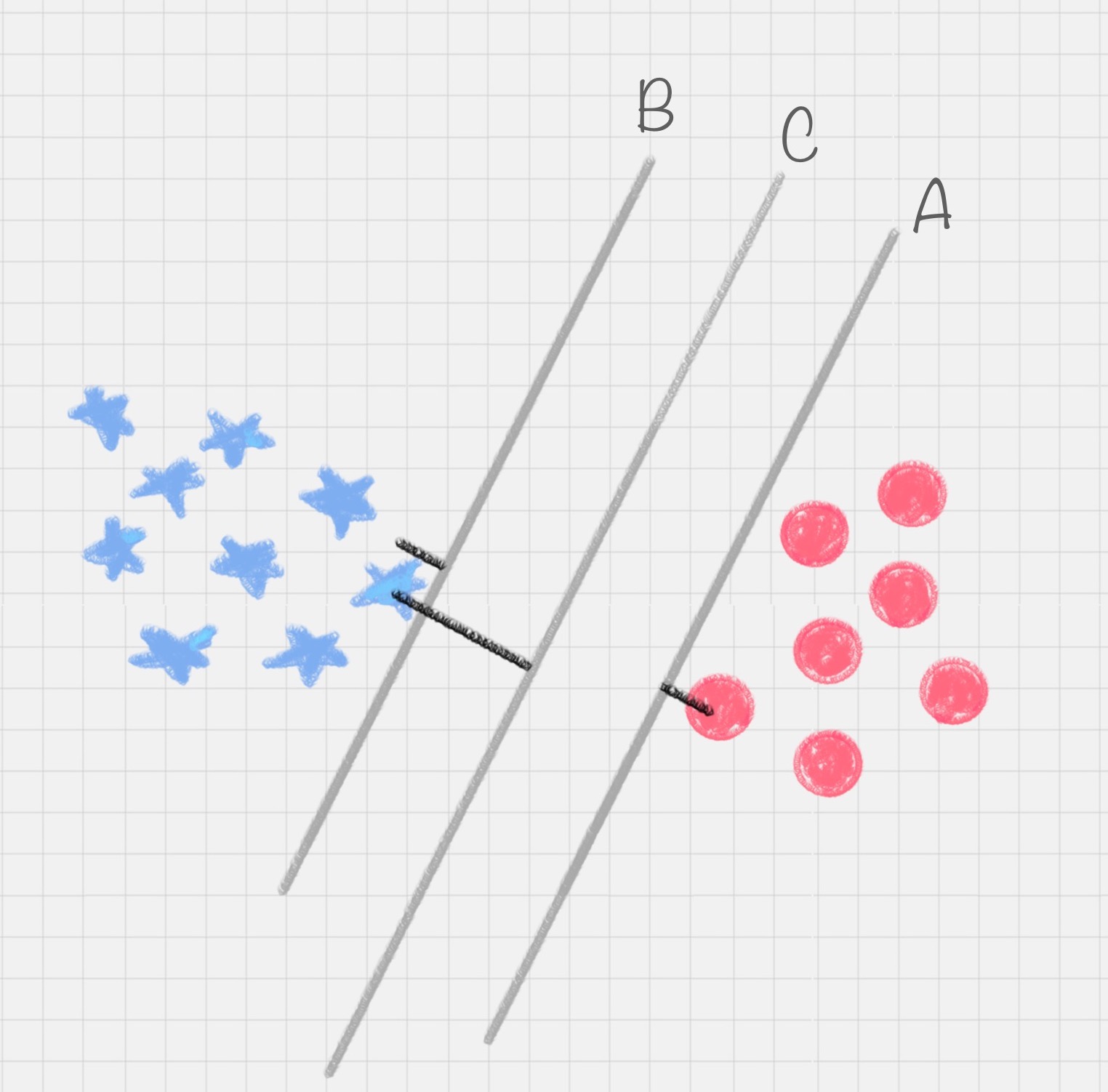
实际上，分类环境不是在二维平面中的，而是在多维空间中，这样直线 C 就变成了决策面 C。
在保证决策面不变，且分类不产生错误的情况下，可以移动决策面 C，直到产生两个极限的位置：如图中的决策面 A 和决策面 B。极限的位置是指，如果越过了这个位置，就会产生分类错误。这样的话，两个极限位置 A 和 B 之间的分界线 C 就是最优决策面。极限位置到最优决策面 C 之间的距离，就是“分类间隔”，英文叫做 margin。
如果转动这个最优决策面，你会发现可能存在多个最优决策面，它们都能把数据集正确分开，这些最优决策面的分类间隔可能是不同的，而那个拥有“最大间隔”（max margin）的决策面就是 SVM 要找的最优解。
SVM 试图把数据集正确地分类，并且间距最大。其中，
- 距离最接近的数据点称为 支持向量（support vector）
- 支持向量定义的沿着分隔线的区域称为 间隔（margin）
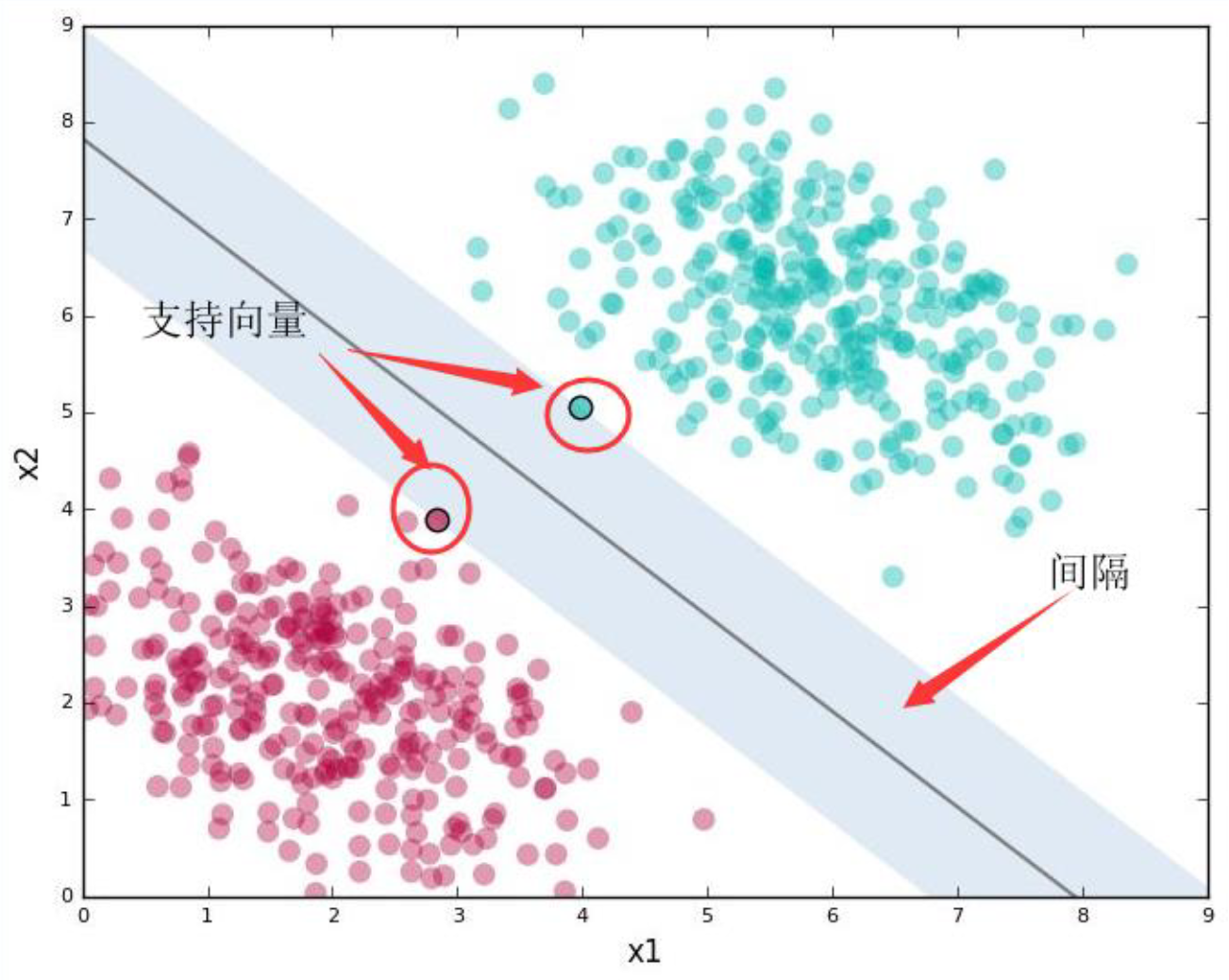
点到超平面的距离公式
超平面的数学表达可以写成：
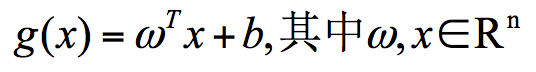
在这个公式里，w、x 是 n 维空间里的向量，其中 x 是函数变量；w 是法向量。法向量这里指的是垂直于平面的直线所表示的向量，它决定了超平面的方向。
SVM 就是帮找到一个超平面，这个超平面能将不同的样本划分开，同时使得样本集中的点到这个分类超平面的最小距离（即分类间隔）最大化。
在这个过程中，支持向量就是离分类超平面最近的样本点，实际上如果确定了支持向量也就确定了这个超平面。所以支持向量决定了分类间隔到底是多少，而在最大间隔以外的样本点，其实对分类都没有意义。
所以说， SVM 就是求解最大分类间隔的过程，还需要对分类间隔的大小进行定义。
首先，定义某类样本集到超平面的距离是这个样本集合内的样本到超平面的最短距离。用 di 代表点 xi 到超平面 wxi+b=0 的欧氏距离。因此要求 di 的最小值，用它来代表这个样本到超平面的最短距离。di 可以用公式计算得出：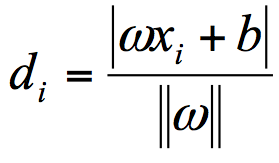
其中||w||为超平面的范数，di 的公式可以用解析几何知识进行推导。
最大间隔的优化模型
目标就是找出所有分类间隔中最大的那个值对应的超平面。在数学上，这是一个凸优化问题（凸优化就是关于求凸集中的凸函数最小化的问题）。通过凸优化问题，最后可以求出最优的 w 和 b，也就是想要找的最优超平面。中间求解的过程会用到拉格朗日乘子，和 KKT（Karush-Kuhn-Tucker）条件。
硬间隔、软间隔
假如数据是完全的线性可分的，那么学习到的模型可以称为硬间隔支持向量机。换个说法，硬间隔指的就是完全分类准确，不能存在分类错误的情况。软间隔，就是允许一定量的样本分类错误。实际工作中的数据没有那么“干净”，或多或少都会存在一些噪点。所以线性可分是个理想情况。这时，需要使用到软间隔 SVM（近似线性可分），比如下面这种情况：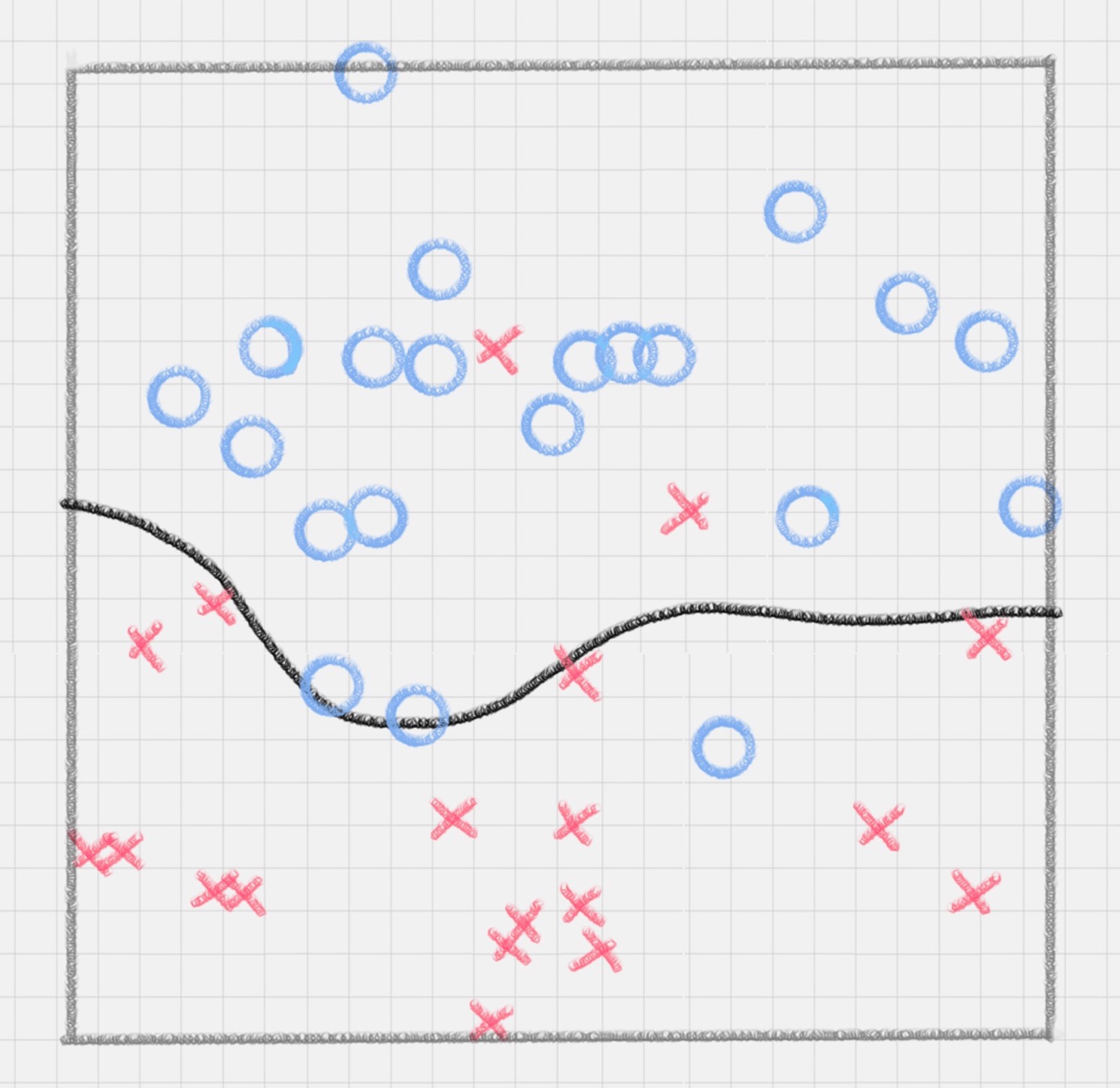
SVM 允许通过参数 C 指定愿意接受多少误差，C 可以指定以下两者的折衷：
- 较宽的间隔
- 正确分类训练数据
C 值较高，意味着训练数据上容许的误差较少。这是一个折衷，以间隔的宽度为代价得到训练数据上更好的分类。
非线性可分数据
比如下面的样本集就是个非线性的数据。图中的两类数据，分别分布为两个圆圈的形状。那么这种情况下，不论是多高级的分类器，只要映射函数是线性的，就没法处理，SVM 也处理不了。这时需要引入一个新的概念：核函数。它可以将样本从原始空间映射到一个更高维的特质空间中，使得样本在新的空间中线性可分。这样就可以使用原来的推导来进行计算，只是所有的推导是在新的空间，而不是在原来的空间中进行。
- 核函数是特征转换函数
- SVM 使用核函数完成数据的投影
- 让SVM 得到普遍应用的关键是投影到高维，这正是核函数的用户之地
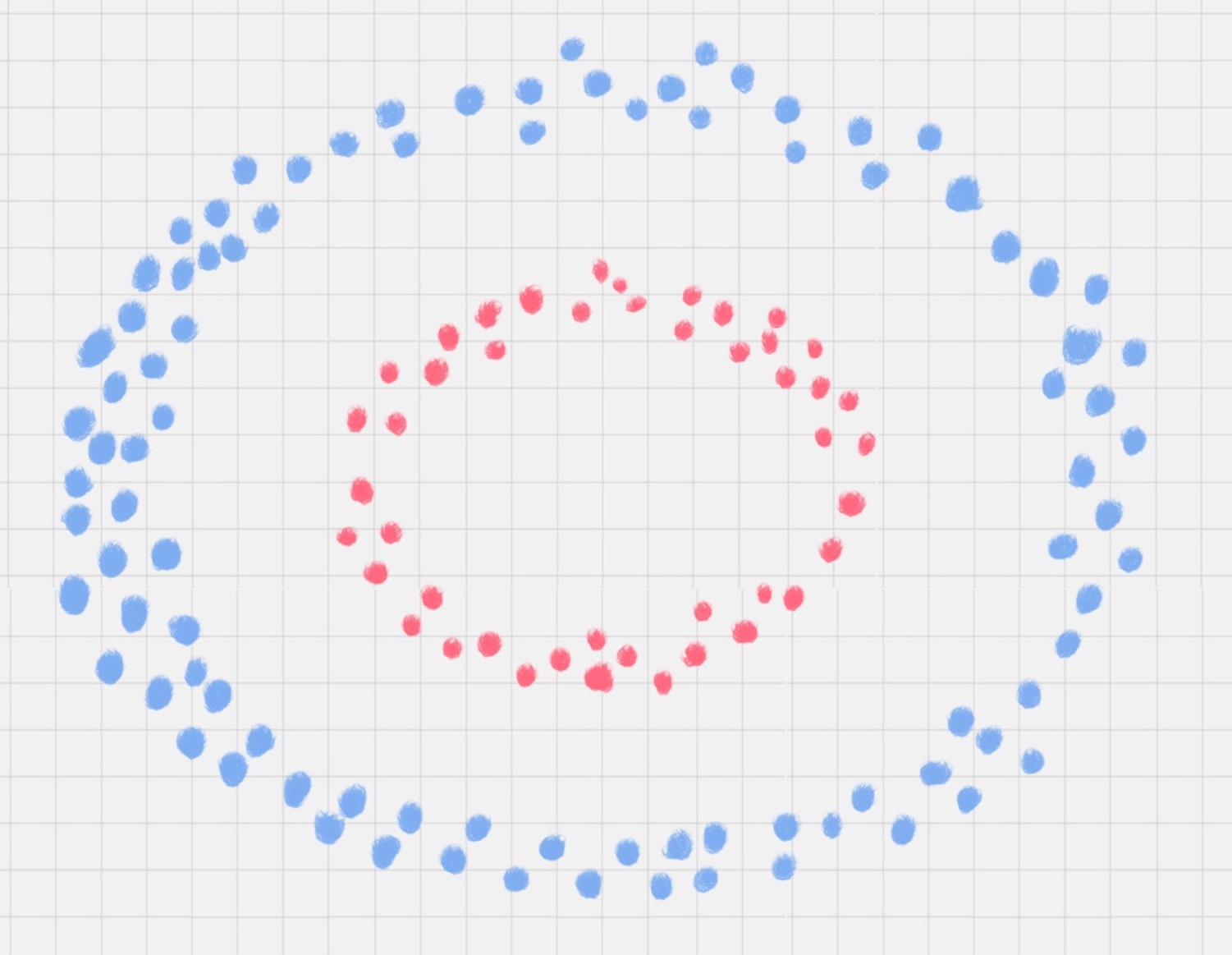
所以在非线性 SVM 中，核函数的选择就是影响 SVM 最大的变量。最常用的核函数有线性核、多项式核、高斯核、拉普拉斯核、sigmoid 核，或者是这些核函数的组合。
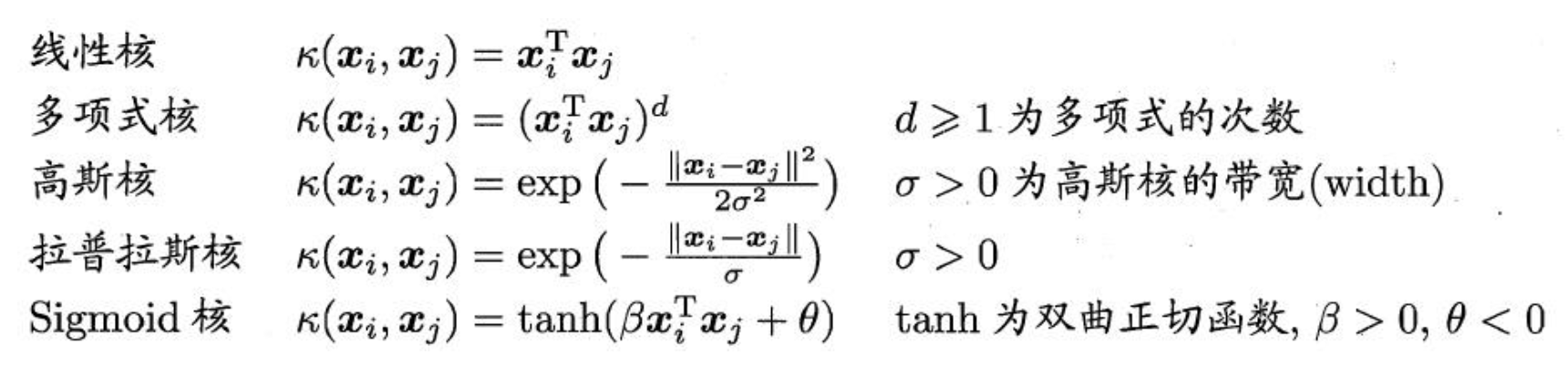
这些函数的区别在于映射方式的不同。通过这些核函数，就可以把样本空间投射到新的高维空间中。当然软间隔和核函数的提出，都是为了方便对上面超平面公式中的 w* 和 b* 进行求解，从而得到最大分类间隔的超平面。
SVM 优点
- SVM 在线性可分的数据上效果极为出色
- 使用正确的 C 值， SVM 在基本线性可分的数据上效果相当出色
- 线性不可分的数据可以通过核函数投影至完美线性可分或基本线性可分的空间，从而将问题转化为 1 或 2
- SVM 在解决小样本、非线性及高维模式识别问题中表现出许多特有的优势
Summary
完全线性可分情况下的线性分类器，也就是线性可分的情况，是最原始的 SVM，它最核心的思想就是找到最大的分类间隔；
大部分线性可分情况下的线性分类器，引入了软间隔的概念。软间隔，就是允许一定量的样本分类错误；
线性不可分情况下的非线性分类器，引入了核函数。它让原有的样本空间通过核函数投射到了一个高维的空间中，从而变得线性可分。