在机器学习中,如果参数很多,而样本数量比较少,很容易产生过拟合问题。因此在函数的损失模型中加入惩罚系数,这些参数一般都会很小,而越小的参数,模型越简单,越不会产生过拟合问题。参考的网页资源为:http://openclassroom.stanford.edu/MainFolder/DocumentPage.php?course=DeepLearning&doc=exercises/ex5/ex5.html
实验原理:
假设对于一个由10个点组成的样本,要拟合一条曲线来表示。如果想采取高次多项式预测表示,如下:
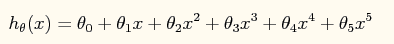
那么现在我们有了模型的六个特征,分别对应的六个预测参数。如果用这个五次多项式去拟合一个只有十个点的样本集,很容易产生过拟合。所以我们引入惩罚参数:
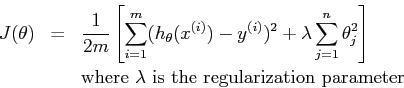
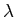 是怎么控制过拟合的呢?它独立于预测参数的平方和,当预测参数很大时,损失函数必然会很大。所以往往预测参数就会很小,在极端情况下,假设第五个参数小到零,则变成四次多项式了,再小呢,最后就有可能接近于二次曲线、乃至直线。这样的话,模型就趋于简单化。有效的控制了过拟合的产生。
是怎么控制过拟合的呢?它独立于预测参数的平方和,当预测参数很大时,损失函数必然会很大。所以往往预测参数就会很小,在极端情况下,假设第五个参数小到零,则变成四次多项式了,再小呢,最后就有可能接近于二次曲线、乃至直线。这样的话,模型就趋于简单化。有效的控制了过拟合的产生。
Normal equations方法:
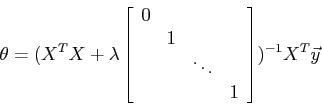
和普通的正则方程法相比,公式左边括号中增加了一个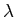 乘以一个(n+1)*(n+1)的矩阵。最左上角是零,剩下的是一个单位对角矩阵。The vector
乘以一个(n+1)*(n+1)的矩阵。最左上角是零,剩下的是一个单位对角矩阵。The vector ![]() and the matrix
and the matrix ![]() 和unregularized regression的定义是一样的:
和unregularized regression的定义是一样的:
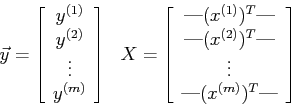
使用这个等式,寻求对于以下三个不同的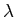 的预测参数:
的预测参数:
a. ![]() (等同于non-regularized linear regression)
(等同于non-regularized linear regression)
b. ![]()
c. ![]()
实验结果如下:
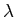 等于10的时候的过拟合的可能性最小。
等于10的时候的过拟合的可能性最小。
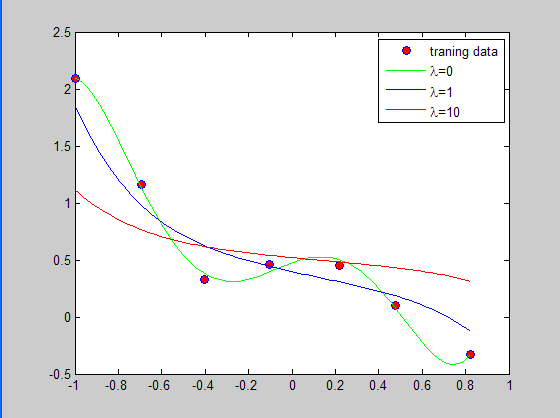
源代码如下:
clc,clear %加载数据 x = load('ex5Linx.dat'); y = load('ex5Liny.dat'); %显示原始数据 plot(x,y,'o','MarkerEdgeColor','b','MarkerFaceColor','r') %将特征值变成训练样本矩阵 x = [ones(length(x),1) x x.^2 x.^3 x.^4 x.^5]; [m n] = size(x); n = n -1; %计算参数sidta,并且绘制出拟合曲线 rm = diag([0;ones(n,1)]);%lamda后面的矩阵 lamda = [0 1 10]'; colortype = {'g','b','r'}; sida = zeros(n+1,3); xrange = linspace(min(x(:,2)),max(x(:,2)))'; hold on; for i = 1:3 sida(:,i) = inv(x'*x+lamda(i).*rm)*x'*y;%计算参数sida norm_sida = norm(sida) yrange = [ones(size(xrange)) xrange xrange.^2 xrange.^3,... xrange.^4 xrange.^5]*sida(:,i); plot(xrange',yrange,char(colortype(i))) hold on end legend('traning data', '\lambda=0', '\lambda=1','\lambda=10')%注意转义字符的使用方法 hold off