对于大量的web pages,不可避免的一个问题就是有很多网页是相似的。比如有些网页只是另一网页的剽窃或者镜像。发现这些相似性是大数据处理的一个问题。
Jaccada距离:
首先,引入一个Jaccad距离来量度两个集合的相似度。定义如下:
两个集合S和T之间的相似度为:|S∩T|/|SUT|。例如:
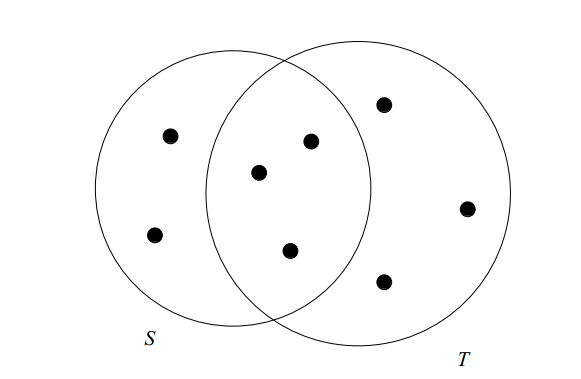
S和T之间的相似度为SIM(S,T)=3/8
利用这个量度可以很好的解决web pages字面上相似的问题,但是显而易见的问题是,如果逐个字母(或者汉字)对比的话,只是字母层面的相似比较。有可能两篇文章的内容很相似,但是表述的方式不一样,也就是meaning 层面的相似。这在处理新闻等网页时,就很重要了。比如说如果谷歌想显示今天的一个新闻,但是新闻内容一样,各个媒体采用的表述不相同而已(但是相似)。对于这类问题,Jaccad距离就不能胜任了。
协同过滤
关于协同过滤参见我在CSDN上转来的一篇文章。需要注意的是,如果Jaccad值越大,我们定义两者之间的相似度越高。对于mirror站点,或许90%以上才能判定为相似。但是对于网上购物,购物行为能达到20%以上就可以判定为具有相似品味的用户了。
Shingling of Documents
表示文档最有效的方式是集合,通过把文档划分为像句子或者短语类似的shingling,将文档划分为片段。具有很多这样相同shingling的,不管位置在哪,判定为文档相似。定义长度为k的字符串为k-shingling。
那么假设有一个文档是abcdabd,选择k为2的话,该文档可用集合{ab,bc,cd,da,bd}表示。注意到ab虽然出现两次但是集合里只记一次。如果遇到空格的话,要忽略掉。
那么怎么选择k呢,如果k为一的话,所有的web pages都有很高的相似度。如果太大的话,任何一个shingling出现在文档中的概率会非常低。根据经验,一般对于邮件设置k=5,对于研究论文等k=9.
Hashing shingling
作为用字符串当shingling的替换,我们可以采用一些哈希函数来把长度为k的字符串映射到一系列的buckets上,然后把bucket当做shingling。
这样做是有好处的。假设k=9,将9-shingling映射到bucket的值将是2^32-1个,也就是说文档将用4 bytes而不是9bytes来表示。(怎么理解?我是这样理解的,有32个包括标点之类的常用字母,有2^32-1中组合,原来用9位来表示,现在用4位,不仅数据压缩了,而且我们可以对single shingling采用位操作了)
signature比较
虽然我们把k-shingling哈希为4bytes的数据,但是要存储一篇文档的空间还是变成了原来的四倍。如果有很多文档的话,这是很耗存储空间的。
那么怎么办呢?
我们需要找到一种signature来表示文档,然后比较signature之间的Jaccad距离。首先我们定义一个sets的矩阵表示。
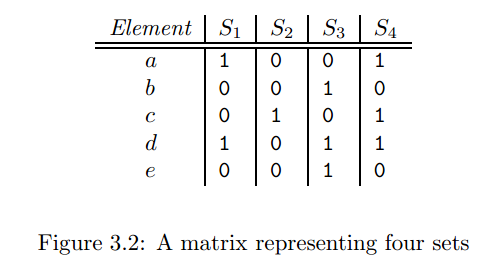
S1={a,d},S2={c},S3={b,d,e}S4={a,c,d} 也就是值为1的话代表这个字母在该S中有出现过。很明显,如果文档都这么存储的话太耗空间了,这不过是一种很好的数据视觉表示而已。
我们把这种矩阵叫做characteristic matrix。
Minhashing
我们想要构建的signature并不是上面的矩阵。于是引入minhash方法。从简单的例子开始:
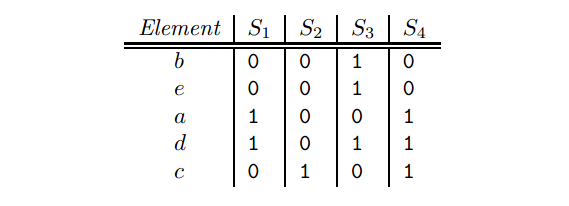
对于这样一个characteristic matrix我们怎么minhash呢?对于S1,从该列的第一行开始,遇到第一个为1的则为哈希值。所以h(S1)=a,同理计算h(S2)=c,h(S3)=b,h(S4)=a.
这时候会出现一个奇妙的特征:P(h(s1)=h(s2))即两个集合哈希值相等的概率会和两者的SIM(s1,s2)相等。作者是这样证明的:将S1,S2的可能组合分为三种均为1或者一个为零一个为1或者均为0,但是均为0没有意义不予考虑。那么定义均为1的个数为x,一个为1另外一个为0的个数为y。那么h(s1)=h(s2)相等的概率为x/x+y,而SIM(s1,s2)也为x/x+y。这个等式在大数据量并且随机的情况下一般性成立。
但是实际上并不是这样minhash的。我们有一种近似的minhash方法。处理过程如下:

第一步初始化如下: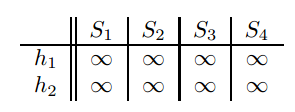
然后看第一行,发现S1,S4的值为1,则变化,其他的不变。变化的值为右边的两列哈希值。矩阵变化成如下:
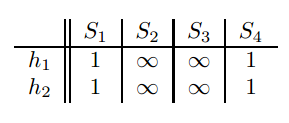
接着看第二行,发现只有S3为1,则只S3变化,矩阵变成如下:
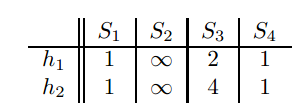
再往下,依次类推,如果哈希值比原来的数大则不变,否则替换为更小的那个。
最后变为: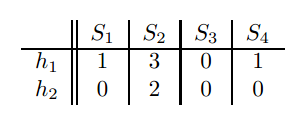
发现矩阵的列数没变但是行数变为了2,也就是哈希函数的个数。此时SIM(S1,S4)为1,因为两者相同嘛。而原来矩阵中SIM(S1,S4)=2/3,按照x/x+y公式计算来的。两者不是很接近。但是这是小数据量情况下,在大数据量情况下,效果是相当的。也就是说用这个signture可以很好的表征文档,然后计算相似度来衡量两个文档是否相似。