一、问题描述:
完全背包:有N种物品和一个容量为V的背包,每种物品都有无限件可用。第i种物品的费用是c[i],价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
多重背包:有N种物品和一个容量为V的背包。第i种物品最多有n[i]件可用,每件费用是c[i],价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
比较这两个题目以及上次谈到的0-1背包(想看0-1背包的请移步:0-1背包),会发现不同点在于每种背包的数量,01背包是每种只有一件,完全背包是每种无限件,而多重背包是每种有限件。
二、完全背包动态规划过程:
根据第i种物品放多少件进行决策,所以状态转移方程为
![]()
其中F[i-1][j-K*C[i]]+K*W[i]表示前i-1种物品中选取若干件物品放入剩余空间为j-K*C[i]的背包中所能得到的最大价值加上k件第i种物品;
设物品种数为N,背包容量为V,第i种物品体积为C[i],第i种物品价值为W[i]。
与01背包相同,完全背包也需要求出NV个状态F[i][j]。但是完全背包求F[i][j]时需要对k分别取0,…,j/C[i]求最大F[i][j]值。
这样代码应该是三层循环(物品数量,物品种类,背包大小这三个循环),伪代码如下:
F[0][] ← {0} F[][0] ← {0} for i←1 to N do for j←1 to V do for k←0 to j/C[i] if(j >= k*C[i]) then F[i][k] ← max(F[i][k],F[i-1][j-k*C[i]]+k*W[i]) return F[N][V]
很明显,这样一般情况下会超时,需要转化成时间复杂度比较低的在进行求解
经过思考可以想到完全背包可以转化为01背包:
因为同种物品可以多次选取,那么第i种物品最多可以选取V/C[i]件价值不变的物品,然后就转化为01背包问题。如果把第i种物品拆成体积为C[i]×2k价值W[i]×2k的物品,其中满足C[i]×2k≤V。即设F[i][j]表示出在前i种物品中选取若干件物品放入容量为j的背包所得的最大价值。那么对于第i种物品的出现,我们对第i种物品放不放入背包进行决策。如果不放那么F[i][j]=F[i-1][j];如果确定放,背包中应该出现至少一件第i种物品,所以F[i][j]种至少应该出现一件第i种物品,即F[i][j]=F[i][j-C[i]]+W[i]。为什么会是F[i][j-C[i]]+W[i]?因为F[i][j-C[i]]里面可能有第i种物品,也可能没有第i种物品。我们要确保F[i][j]至少有一件第i件物品,所以要预留C[i]的空间来存放一件第i种物品。
状态方程为:
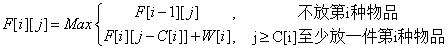
0-1背包和完全背包的不同:
从二维数组上区别0-1背包和完全背包也就是状态转移方程就差别在放第i中物品时,完全背包在选择放这个物品时,最优解是F[i][j-c[i]]+w[i]即画表格中同行的那一个,而0-1背包比较的是F[i-1][j-c[i]]+w[i],上一行的那一个。
从一维数组上区别0-1背包和完全背包差别就在循环顺序上,0-1背包必须逆序,因为这样保证了不会重复选择已经选择的物品,而完全背包是顺序,顺序会覆盖以前的状态,所以存在选择多次的情况,也符合完全背包的题意。状态转移方程都为F[i] = max(F[i],dp[F-c[i]]+v[i])。
三、完全背包代码
用一维数组实现
#include<cstdio> #include<algorithm> using namespace std; int w[300],c[300],f[300010]; int V,n; int main() { scanf("%d%d",&V,&n); for(int i=1; i<=n; i++) { scanf("%d%d",&w[i],&c[i]); } for(int i=1; i<=n; i++) for(int j=w[i]; j<=V; j++)//注意此处,与0-1背包不同,这里为顺序,0-1背包为逆序 f[j]=max(f[j],f[j-w[i]]+c[i]); printf("max=%d ",f[V]); return 0; }
四、多重背包动态规划过程:
多重背包问题的思路跟完全背包的思路非常类似,只是k的取值是有限制的,因为每件物品的数量是有限制的,状态转移方程为:
dp[i][v] = max{dp[i - 1][v - k * c[i]] + w[i] | 0 <=k <= n[i]}
其中c[i]是物品的数量,和完全背包的不同支出在于完全背包可以取无数件,而多重背包给定了最多能取的数量。这样也是三个循环,分别是背包容量,物品个数和物品种类。这样如果数量比较多的情况,很明显这个做法也会超时,所以我们也要想更优化的方法去完善。
转化为01背包问题
转化为01背包求解:把第i种物品换成n[i]件01背包中的物品。考虑二进制的思想,考虑把第i种物品换成若干件物品,使得原问题中第i种物品可取的每种策略——取0..n[i]件——均能等价于取若干件代换以后的物品。另外,取超过n[i]件的策略必不能出现。
方法是:将第i种物品分成若干件物品,其中每件物品有一个系数,这件物品的费用和价值均是原来的费用和价值乘以这个系数。使这些系数分别为1,2,4,...,2^(k-1),n[i]-2^k+1,且k是满足n[i]-2^k+1>0的最大整数。例如,如果n[i]为13,就将这种物品分成系数分别为1,2,4,6的四件物品。
分成的这几件物品的系数和为n[i],表明不可能取多于n[i]件的第i种物品。另外这种方法也能保证对于0..n[i]间的每一个整数,均可以用若干个系数的和表示,证明我也没看过这里就不贴上了,主要还是需要去理解代码,代码在下面给出。
五、多重背包代码:
#include <stdio.h> #include <iostream> #include <algorithm> #include <cstring> #define MAX 1000000 using namespace std; int dp[MAX];//存储最后背包最大能存多少 int value[MAX],weight[MAX],number[MAX];//分别存的是物品的价值,每一个的重量以及数量 int bag; void ZeroOnePack(int weight,int value )//01背包 { int i; for(i = bag; i>=weight; i--) { dp[i] = max(dp[i],dp[i-weight]+value); } } void CompletePack(int weight,int value)//完全背包 { int i; for(i = weight; i<=bag; i++) { dp[i] = max(dp[i],dp[i-weight]+value); } } void MultiplePack(int weight,int value,int number)//多重背包 { if(bag<=number*weight)//如果总容量比这个物品的容量要小,那么这个物品可以直到取完,相当于完全背包 { CompletePack(weight,value); return ; } else//否则就将多重背包转化为01背包 { int k = 1; while(k<=number) { ZeroOnePack(k*weight,k*value); number = number-k; k = 2*k;//这里采用二进制思想 } ZeroOnePack(number*weight,number*value); } } int main() { int n; while(~scanf("%d%d",&bag,&n)) { int i,sum=0; for(i = 0; i<n; i++) { scanf("%d",&number[i]);//输入数量 scanf("%d",&value[i]);//输入价值 此题没有物品的重量,可以理解为体积和价值相等 } memset(dp,0,sizeof(dp)); for(i = 0; i<n; i++) { MultiplePack(value[i],value[i],number[i]);//调用多重背包,注意穿参的时候分别是重量,价值和数量 } cout<<dp[bag]<<endl; } return 0; }