一、含义
从源点到经过的所有路径的最终到达汇点的所有流量和
例如:
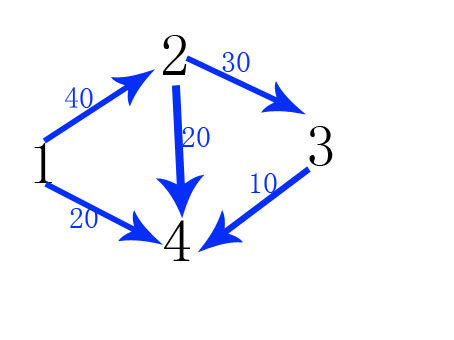
在这个图中求源点1,到汇点4的最大流。答案为50,其中1->2->4为20 ;1->4为20 ;1->2->3->4为10;总和为20+20+10=50。
二、EK算法的核心
反复寻找源点s到汇点t之间的增广路径,若有,找出增广路径上每一段[容量-流量]的最小值delta,若无,则结束。
在寻找增广路径时,可以用BFS来找,并且更新残留网络的值(涉及到反向边)。
而找到delta后,则使最大流值加上delta,更新为当前的最大流值。
对于BFS找增广路:
1. flow[1]=INF,pre[1]=0;
源点1进队列,开始找增广路,
capacity[1][2]=40>0,则flow[2]=min(flow[1],40)=40;
capacity[1][4]=20>0,则flow[4]=min(flow[1],20)=20;
capacity[2][3]=30>0,则flow[3]=min(folw[2]=40,30)=30;
capacity[2][4]=30,但是pre[4]=1(已经在capacity[1][4]这遍历过4号点了)
capacity[3][4].....
当index=4(汇点),结束增广路的寻找
传递回increasement(该路径的流),利用前驱pre寻找路径
路径也自然变成了这样:

2.flow[1]=INF,pre[1]=0;
源点1进队列,开始找增广路,
capacity[1][2]=40>0,则flow[2]=min(flow[1],40)=40;
capacity[1][4]=0!>0,跳过
capacity[2][3]=30>0,则flow[3]=min(folw[2]=40,30)=30;
capacity[2][4]=30,pre[4]=2,则flow[2][4]=min(flow[2]=40,20)=20;
capacity[3][4].....
当index=4(汇点),结束增广路的寻找
传递回increasement(该路径的流),利用前驱pre寻找路径
图也被改成

接下来同理
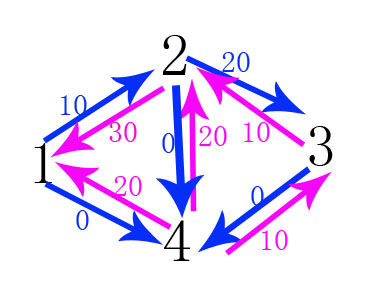
这就是最终完成的图,最终sumflow=20+20+10=50(这个就是最大流的值)
PS,为什么要有反向边呢?

我们第一次找到了1-2-3-4这条增广路,这条路上的delta值显然是1。于是我们修改后得到了下面这个流。(图中的数字是容量)

这时候(1,2)和(3,4)边上的流量都等于容量了,我们再也找不到其他的增广路了,当前的流量是1。
但这个答案明显不是最大流,因为我们可以同时走1-2-4和1-3-4,这样可以得到流量为2的流。
那么我们刚刚的算法问题在哪里呢?问题就在于我们没有给程序一个”后悔”的机会,应该有一个不走(2-3-4)而改走(2-4)的机制。那么如何解决这个问题呢?回溯搜索吗?那么我们的效率就上升到指数级了。
而这个算法神奇的利用了一个叫做反向边的概念来解决这个问题。即每条边(I,j)都有一条反向边(j,i),反向边也同样有它的容量。
我们直接来看它是如何解决的:
在第一次找到增广路之后,在把路上每一段的容量减少delta的同时,也把每一段上的反方向的容量增加delta。即在Dec(c[x,y],delta)的同时,inc(c[y,x],delta)
我们来看刚才的例子,在找到1-2-3-4这条增广路之后,把容量修改成如下
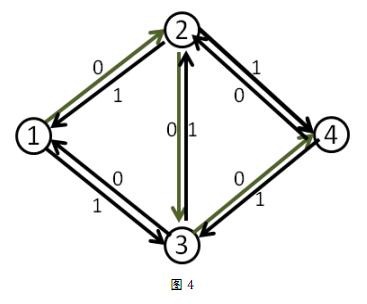
这时再找增广路的时候,就会找到1-3-2-4这条可增广量,即delta值为1的可增广路。将这条路增广之后,得到了最大流2。

那么,这么做为什么会是对的呢?我来通俗的解释一下吧。
事实上,当我们第二次的增广路走3-2这条反向边的时候,就相当于把2-3这条正向边已经是用了的流量给”退”了回去,不走2-3这条路,而改走从2点出发的其他的路也就是2-4。(有人问如果这里没有2-4怎么办,这时假如没有2-4这条路的话,最终这条增广路也不会存在,因为他根本不能走到汇点)同时本来在3-4上的流量由1-3-4这条路来”接管”。而最终2-3这条路正向流量1,反向流量1,等于没有流量。
这就是这个算法的精华部分,利用反向边,使程序有了一个后悔和改正的机会。而这个算法和我刚才给出的代码相比只多了一句话而已。
至此,最大流Edmond-Karp算法介绍完毕。
三、代码:
/*poj1273*/ #include <iostream> #include <cstdlib> #include <algorithm> #include <string> #include <cstring> #include <stdio.h> #include <queue> #define IO ios::sync_with_stdio(false); cin.tie(0); cout.tie(0); using namespace std; const int MAX=1000000; int map[205][205],flow[205],pre[205],n,m; bool vis[205]; int BFS() { int up; queue<int> q; vis[1]=1; memset(pre,-1,sizeof(pre)); memset(vis,0,sizeof(vis)); for(int i=1; i<=n; i++) flow[i]=MAX; q.push(1); while(!q.empty()) { up=q.front(); q.pop(); if(up==n) break; for(int i=1; i<=n; i++) { if(!vis[i]&&map[up][i]>0) { vis[i]=1; flow[i]=min(flow[up],map[up][i]); pre[i]=up; q.push(i); } } } if(!vis[n]||n==1) return -1; return flow[n]; } int EK() { int d,maxflow=0,up,down; maxflow=0; while((d=BFS())!=-1) { maxflow+=d; down=n; while(down!=1) { up=pre[down]; map[up][down]-=d; map[down][up]+=d; down=up; } } return maxflow; } int main() { while(~scanf("%d%d",&m,&n)) { memset(map,0,sizeof(map)); int a,b,c; for(int i=1; i<=m; i++) { scanf("%d%d%d",&a,&b,&c); map[a][b]+=c; } printf("%d ",EK());//输出从1到n号点的最大流 } return 0; }