三角形面积并「CQOI2005」

【题目描述】 给出$n$个三角形，求它们并的面积。

【输入格式】 第一行为$n(n leq 100)$，即三角形的个数 以下$n$行，每行$6$个整数$x_1, y_1, x_2, y_2, x_3, y_3$，代表三角形的顶点坐标。坐标均为不超过$10^6$

【输出格式】 输出并的面积$u$, 保留两位小数。

题解

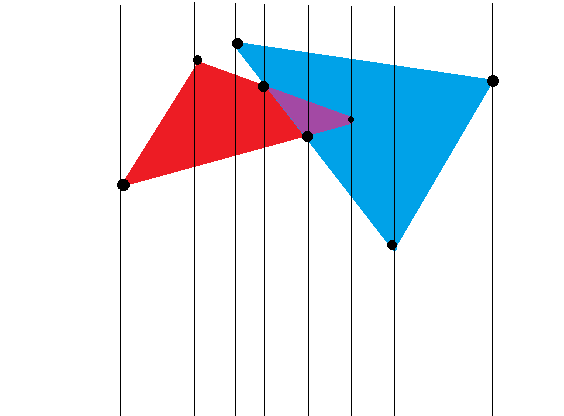
我们把三角形的所有顶点和所有交点全部抠出来 然后过每一个点作一条平行于y轴的直线

容易发现 任意相邻两条直线之间的有效面积都是一个(也可能是多个)三角形或矩形的面积

所以 只要我们求出左边那条直线穿过三角形的长度$ld$和右边那条直线的$rd$，那么总面积就加上$frac{(ld+rd)*(x_r-x_l)}{2}$就好啦！

怎么求？具体来说 就是对于每个三角形分别求出这条线$x=k$穿过它的范围$[a,b]$，然后区间求并即可

怎么求？对于每个三角形 算出这条线和它的三边有几个交点 如果是3个交点就说明这条线过它的一个顶点 如果2个就说明穿过了两条边 如果0个或1个就不用管这个三角形了

万一有一个三角形有一条边也平行于y轴 与某条直线产生了无数个交点呢？

注意到答案保留两位小数就可以了 我们可以用一些奇技♂淫巧

把那种与y轴平行的三角形边稍稍倾斜一个小角度即可 对面积的影响微乎其微

至于求交点那些建议用计算几何算 避免被卡精度

代码

#include <bits/stdc++.h>
using namespace std;

const double eps = 1e-8;
inline int sgn(double x) {
    if (fabs(x) < eps) return 0;
    return (x < 0) ? -1 : 1;
}
struct point{
    double x, y;
    point(double xx = 0.0, double yy = 0.0): x(xx), y(yy) {}
};
typedef point vec;

struct edge{
	point a, b;
	edge(point aa = point(), point bb = point()): a(aa), b(bb) {}
};

inline vec operator + (vec A, vec B) {
    return vec(A.x + B.x, A.y + B.y);
}
inline vec operator - (point A, point B) {
    return vec(A.x - B.x, A.y - B.y);
}
inline vec operator * (vec A, double p) {
    return vec(A.x * p, A.y * p);
}
inline vec operator / (vec A, double p) {
    return vec(A.x / p, A.y / p);
}
inline bool operator < (const point A, const point B) {
    return A.x < B.x || (sgn(A.x - B.x) == 0 && A.y < B.y);
}
inline double dot(vec A, vec B) {
    return A.x * B.x + A.y * B.y;
}
inline double cross(vec A, vec B) {
    return A.x * B.y - A.y * B.x;
}
inline point line_intersection(point P, point P2, point Q, point Q2) { //求交点 
	vec v = P - P2, w = Q - Q2;
	vec u = P - Q;
    double t = cross(w, u) / cross(v, w);
    return P + v * t;
}
inline bool GFXJ(point A, point B, point P, point Q) { //规范相交 
    double c1 = cross(B - A, P - A), c2 = cross(B - A, Q - A);
    double c3 = cross(Q - P, A - P), c4 = cross(Q - P, B - P);
    if (sgn(cross(B - A, P - A)) == 0) return 0;
    return sgn(c1) * sgn(c2) < 0 && sgn(c3) * sgn(c4) < 0;
}
inline bool BGFXJ(point A, point B, point P, point Q) { //不规范相交 
    double c1 = cross(B - A, P - A), c2 = cross(B - A, Q - A);
    double c3 = cross(Q - P, A - P), c4 = cross(Q - P, B - P);
    if (sgn(cross(B - A, P - A)) == 0) return 0;
    return sgn(c1) * sgn(c2) <= 0 && sgn(c3) * sgn(c4) <= 0;
}

int n, tot, ee;
double ans;
point p[100005];
edge e[305];
vector<pair<double, double> > sol;

double solve(double x) {
	sol.clear();
	point pp = point(x, -2e6); point q = point(x, 2e6);
	for (int i = 1; i <= ee; i += 3) {
		if (BGFXJ(pp, q, e[i].a, e[i].b) + BGFXJ(pp, q, e[i+1].a, e[i+1].b) + BGFXJ(pp, q, e[i+2].a, e[i+2].b) < 2) {
			continue;
		}
		pair<double, double> tmp;
		tmp.first = 2e6, tmp.second = -2e6;
		for (int j = 0; j <= 2; j++) {
			if (BGFXJ(pp, q, e[i+j].a, e[i+j].b)) {
				double now = line_intersection(pp, q, e[i+j].a, e[i+j].b).y;
				tmp.first = min(tmp.first, now);
				tmp.second = max(tmp.second, now);
			}
		}
		sol.push_back(tmp);
	}
	sort(sol.begin(), sol.end());
	if (!sol.size()) return 0;
	double lst = sol[0].first, ret = 0;
	for (int i = 0; i < sol.size(); i++) {
		if (sol[i].second <= lst) continue;
		if (sol[i].first > lst) ret += sol[i].second - sol[i].first;
		else ret += sol[i].second - lst;
		lst = sol[i].second;
	}
	return ret;
}

int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) {
		scanf("%lf %lf %lf %lf %lf %lf", &p[tot+1].x, &p[tot+1].y, &p[tot+2].x, &p[tot+2].y, &p[tot+3].x, &p[tot+3].y);
		if (p[tot+1].x == p[tot+2].x) p[tot+2].x += 0.001;
		else if (p[tot+1].x == p[tot+3].x) p[tot+3].x += 0.001;
		else if (p[tot+2].x == p[tot+3].x) p[tot+3].x += 0.001;
		e[++ee] = edge(p[tot+1], p[tot+2]);
		e[++ee] = edge(p[tot+2], p[tot+3]);
		e[++ee] = edge(p[tot+3], p[tot+1]);
		tot += 3;
	}
	for (int i = 1; i <= ee; i++) {
		for (int j = i + 1; j <= ee; j++) {
			if (GFXJ(e[i].a, e[i].b, e[j].a, e[j].b)) {
				p[++tot] = line_intersection(e[i].a, e[i].b, e[j].a, e[j].b);
			}
		}
	}
	sort(p + 1, p + tot + 1);
	double lst = 0, lstx = 114514, now = 0;
	for (int i = 1; i <= tot; i++) {
		now = solve(p[i].x);
		if (sgn(lstx - 114514) != 0) {
			ans += (p[i].x - lstx) * (now + lst) / 2;
		}
		lstx = p[i].x;
		lst = now;
		while (p[i+1].x == p[i].x) i++;
	} 
	printf("%.2lf
", ans);
	return 0;
}