题目描述
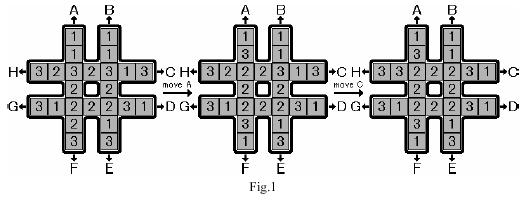
如下图所示,有一个"#"形的棋盘,上面有1,2,3三种数字各8个。给定8种操作,分别为图中的A~H。这些操作会按照图中字母和箭头所指明的方向,把一条长为8的序列循环移动1个单位。例如下图最左边的"#"形棋盘执行操作A后,会变为下图中间的"#"形棋盘,再执行操作C后会变成下图最右边的"#"形棋盘。给定一个初始状态,请使用最少的操作次数,使"#"形棋盘最中间的8个格子里的数字相同。
输入格式
输入包括不超过 30组测试数据。每个测试数据只包括一行,包含 24个整数,每相邻两个整数之间用 1个空格隔开,表示这个 “#” 形棋盘的初始状态。(这些整数的排列顺序是从上至下,同一行的从左至右。例如1 1 1 1 3 2 3 2 3 1 3 2 2 3 1 2 2 2 3 1 2 1 3 3 表示图 1 最左边的状态。)每两组测试数据之间没有换行符。输入文件以一行 0结束。
输出格式
对于每组测试数据,输出两行。第一行用字符A∼H 输出操作的方法,每两个操作字符之间没有空格分开,如果不需要任何步数,输出 No moves needed。第二行输出最终状态中最中间的 8个格子里的数字。如果有多组解,输出操作次数最少的一组解;如果仍有多组解,输出字典序最小的一组。任意相邻两组测试数据的输出之间不需输出换行符。
这么复杂的题......搜索吧
当前的状态可以表示为:当前的棋盘、操作序列和操作次数。前两个可以开全局变量来存。
考虑剪枝:
1.上下界剪枝:
上界:不好找
下界:最好的情况就是当前棋盘的中间8个格子和目标状态的中间8个格子有多少不相同,即
[sum_{i=0}^{7}[g[ctr[i]]≠des[ctr[i]]]
]
其中ctr为center,表示中间格子。然而这个下界对剪枝没什么用
2.搜索顺序优化:不好优化
3.排除等效冗余:正着交换一遍再反着交换一遍是没有意义的,所以我们应该避免做与上一次相反的操作。
4.最优化剪枝:设当前的答案为ans,那么当搜索深度>ans时就没必要搜了。
5.记忆化:日常没有什么好记
并没有剪掉多少对不对。然而这题的答案并不大,我们可以考虑用迭代加深来优化DFS。
从1开始枚举搜索深度,由于IDFS第一次搜到的答案必定为最优解,所以当搜到答案之后就可以退出。那么最优化剪枝就没必要写了。
然而我们加了一个优化的同时扔掉了一个剪枝,实际效果并不明显。那么当我们搜到答案的深度时仍然要面对一棵庞大的搜索树。
由于IDFS第一次搜到答案时就可以直接退出,我们只需要让程序更快地搜到答案,即尽可能往答案所在的方向走。那么我们加一个IDA * 即可。
设计估价函数。结合上面提到的下界,我们可以设计这样一个估价函数:
[f(g[])=sum_{i=0}^{7}[g[ctr[i]]≠des[ctr[i]]]
]
当当前深度加上预估值>当前最大深度时就没必要往下搜了。
#include<iostream>
#include<cstring>
#include<cstdio>
#define maxn
using namespace std;
const int pos[8][7]={{0,2,6,11,15,20,22},{1,3,8,12,17,21,23},{10,9,8,7,6,5,4},{19,18,17,16,15,14,13},{23,21,17,12,8,3,1},{22,20,15,11,6,2,0},{13,14,15,16,17,18,19},{4,5,6,7,8,9,10}};
const int ctr[8]={6,7,8,11,12,15,16,17};
const int a[9]={5,4,7,6,1,0,3,2,-1};
int g[24]; bool flag;
char op['L'+'z'+'s'];
inline int evaluate(){
int cnt[4]={0,0,0,0};
for(register int i=0;i<8;i++) cnt[g[ctr[i]]]++;
return 8-max(cnt[1],max(cnt[2],cnt[3]));
}
inline void change(const int &d){
register int tmp=g[pos[d][0]];
for(register int i=0;i<6;i++) g[pos[d][i]]=g[pos[d][i+1]];
g[pos[d][6]]=tmp;
}
void IDAstar(int dep,int pre_dir,const int &maxdep){
if(flag) return;
if(dep>maxdep||dep+evaluate()>maxdep) return;
if(!evaluate()){
flag=true,op[dep]='�';
printf("%s
%d
",op,g[ctr[0]]);
return;
}
for(register int i=0;i<8;i++)if(i!=a[pre_dir]){
change(i);
op[dep]=i+'A';
IDAstar(dep+1,i,maxdep);
change(a[i]);
}
}
int main(){
while(0127){
flag=false;
for(register int i=0;i<24;i++){
scanf("%d",&g[i]);
if(!g[i]) return 0;
}
if(!evaluate()){ printf("No moves needed
%d
",g[ctr[0]]); continue;}
for(int maxdep=1;!flag;maxdep++) IDAstar(0,8,maxdep);
}
}