快速排序,对于n个数的输入数组,最坏情况运行时间:Θ(n^2);期望运行时间:Θ(nlgn);就地排序(Sort in place)。
数组A[p..r]会被分为两个子数组A[p..q-1]和A[q+1..r],其中A[p..q-1]的元素都不大于A[q],A[q+1..r]都不小于A[q]。
如何划分子数组对运行时间的有很大影响,最坏的情况为n个数的数组划分为一个n-1的数组和一个0元素的数组;最佳情况为对半分(1:1);对于平均情况的划分,其运行时间与最佳情况很接近。
先看代码实现:
快速排序的关键是数组划分,对子数组进行就地重排。

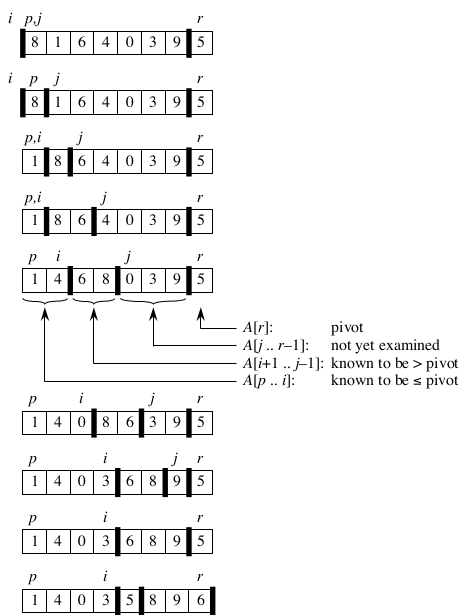
1 /* 2 * 调用划分函数,使得子数组顺序重排 3 */ 4 void quick_sort(int A[], int p, int r){ 5 if(p < r){ 6 int q = partition(A, p, r); 7 quick_sort(A, p, q-1); 8 quick_sort(A, q+1, r); 9 } 10 } 11 12 /* 13 * 对于比x值小的元素通过交换放置到小于x值的区域。 14 * 最后将大于x值的区域的第一个元素与x值,即原A[r],交换 15 * 该下标即为q,形成两个符合要求的数组(A[p..q-1]的元素都不大于A[q],A[q+1..r]都不小于A[q]) 16 */ 17 int partition(int A[], int p, int r){ 18 int x = A[r]; 19 int i = p - 1; 20 int j; 21 for(j = p; j <= r-1; j++){ 22 if(A[j] <= x){ 23 i++; 24 int temp = A[i]; 25 A[i] = A[j]; 26 A[j] = temp; 27 } 28 } 29 int temp = A[i+1]; 30 A[i+1] = A[r]; 31 A[r] = temp; 32 return i+1; 33 }
其中partition的运行时间为Θ(n),n = r-p+1,循环的次数为r-1-p;
过程图如下:
练习7.1-2
当数组A[p..r]中的元素均相同时,partition返回的q值是多少?修改partition,使得数组A[p..r]中的元素均相同时, q = floor((p+r)/2)
当数组A[p..r]中的元素均相同时,partition返回的q值是r;修改很简单,直接判断返回的q值是否与r相同,相同就返回 floor((p+r)/2)。
经网友提醒这种方法判断元素是否全部相同存在错误。。。。。日后再补上。。。囧。。。。
快速排序的性能
快速排序的运行时间与划分数组是否对称有关。如果划分是对称,从渐近意义上讲,与合并排序一样快,否则就与插入排序一样慢。
最坏情况为划分一个n-1个元素的子数组和一个0个元素的子数组。(最大程度不对称)。划分运行时间为Θ(n)。如果对一个0个元素的数组进行递归调用,运行时间为Θ(1).
递归式为:T(n) = T(n-1) + T(0) + Θ(n) = T(n-1) + Θ(n)。通过代换法可证明T(n) = Θ(n^2) (练习7.2-1)
证明:先假设C1(n-1)^2 <= T(n-1) <= C2(n-1)^2成立
则C1(n-1)^2 + Θ(n) <= T(n-1) + Θ(n) <= C2(n-1)^2 + Θ(n)
C1n^2 -C1(2n - 1) + Θ(n) <= T(n-1) + Θ(n) <= C2n^2 -C2(2n - 1) + Θ(n)
我们可以选择合适的常数C1、C2使得C1(2n - 1)、C2(2n - 1)支配Θ(n)。因此可以得出T(n) = Θ(n^2)。
注意,当输入数组完全排好序(升降序一样)和所有元素都是相同的值时,运行时间为Θ(n^2),因为每次划分都是最大程度不对称。画画图,过一遍就会知道。
最佳情况为划分的两个子数组大小为floor(n/2)和ceiling(n/2)-1。
递归式为:T(n) <= 2T(n/2) + Θ(n)。该递归式的解为:T(n) = O(nlgn)
直接通过主定理的情况2得出。
平均情况运行时间更接近最佳情况而不是最坏情况。任一种按常数进行划分都会产生深度为Θ(lgn)的递归书,每一层的总代价为O(n),因此运行时间为O(nlgn)。
从下图看可以更加明显
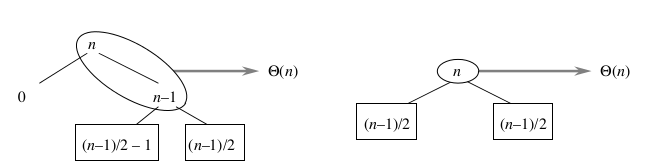
最坏情况的划分之后最佳情况划分的总代价与直接最佳情况的总代价都为Θ(n)。
练习7.2-5
假设快速排序的每一层,所做划分比例都是1-a:a,其中0<a<=1/2是个常数。证明:在对应的递归树中,叶结点的最小深度大约是-lgn/lga,最大深度大约是-lgn/lg(1-a)。
最小深度为每次划分后都是选择最小的一部分继续往下走,每次乘以a。一次迭代减少的元素数从n到an,迭代m次直到剩下的元素为1。
则(a^m)*n = 1, a^m = 1/n,取对数得mlga = -lgn,m = -lgn/lga。
同理可得((1-a)^M)*n = 1,M = -lgn/lg(1-a)。
快速排序随机化版本
便于对于所有输入,均能获得较好的平均情况性能。

1 int randomized_partition(int A[], int p, int r){ 2 int i = p + rand() % (r - p + 1); 3 int temp = A[r]; 4 A[r] = A[i]; 5 A[i] = temp; 6 return partition(A, p, r); 7 } 8 9 int partition(int A[], int p, int r){ 10 int x = A[r]; 11 int i = p - 1; 12 int j; 13 for(j = p; j <= r-1; j++){ 14 if(A[j] <= x){ 15 i++; 16 int temp = A[i]; 17 A[i] = A[j]; 18 A[j] = temp; 19 } 20 } 21 int temp = A[i+1]; 22 A[i+1] = A[r]; 23 A[r] = temp; 24 return i+1; 25 } 26 27 void randomized_quick_sort(int A[], int p, int r){ 28 if(p < r){ 29 int q = randomized_partition(A, p, r); 30 randomized_quick_sort(A, p, q-1); 31 randomized_quick_sort(A, q+1, r); 32 } 33 }
练习7.3-2
在randomized-quicksort的运行过程中,最坏情况下对随机数产生器random调用了多少次?最佳情况调用了多少次?
都为Θ(n)。
快速排序的分析
算导关于快排分析得很详细,数学太差了,看了很多遍才明白一点点,日后一定要继续努力,争取用自己的语言表达出来。
练习7.4-2
证明:快速排序的最佳情况运行时间为Ω(nlgn)

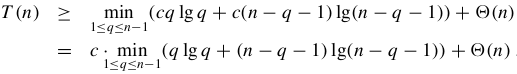
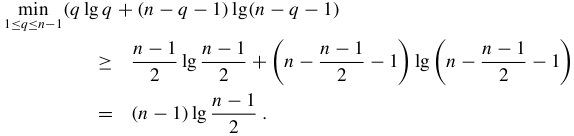
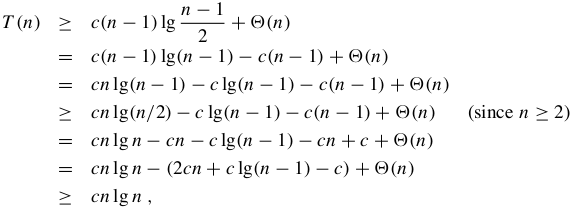
Hoare划分快速排序
划分方式有些不一样;前面的partition划分是将主元值与围绕它划分形成的两部分分隔开来。而Hoare划分则总是将主元值放入到两个划分的子数组里。

1 int hoare_partition(int A[], int p, int r){ 2 int x = A[p]; 3 int i = p; 4 int j = r; 5 6 while(i < j){ 7 while(i < j && A[j] > x) 8 j--; 9 A[i] = A[j]; 10 while(i < j && A[i] < x) 11 i++; 12 A[j] = A[i]; 13 } 14 A[i] = x; 15 return j; 16 } 17 18 void hoare_quick_sort(int A[], int p, int r){ 19 if(p < r){ 20 int q = hoare_partition(A, p, r); 21 hoare_quick_sort(A, p, q-1); 22 hoare_quick_sort(A, q+1, r); 23 } 24 }
继续努力。。。
