Fourier级数
Fourier级数的作用
Fourier级数可以将具有周期性的函数分解为不同频率正弦函数的累加和,从而将时域信号转换到频域,从而得到不同频率的成分在信号中的权重,如下图所示方波的分解(图来自Wikipedia)
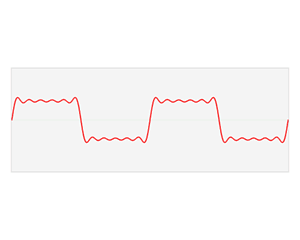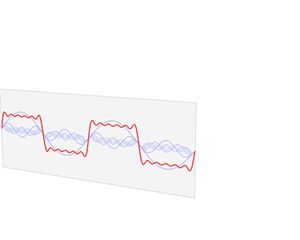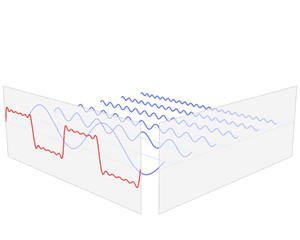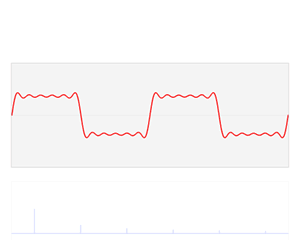
Fourier级数的形式
对于任意一个周期为(T)的周期函数(f(x)),它的Fourier级数表示为下述形式:
[f(x)sim frac {a_0}2+sum_{n=1}^{infty}(a_ncos(frac {2pi nx}{T})+b_nsin(frac{2pi nx}{T}))
]
其中:
[�egin{aligned}
a_n&=frac 2 T int^{T}_{0}f(x)cos(frac {2pi nx}{T}){
m d}x, nin {mathbb N}\
b_n&=frac 2 T int^{T}_{0}f(x)sin(frac {2pi nx}{T}){
m d}x, nin {mathbb N}_+
end{aligned}
]
Fourier级数的收敛条件
Dirichlet条件
若函数(f(x))满足下列条件,则(f(x))的Fourier级数收敛到([f(x+0)+f(x-0)]/2).(充分非必要)
(1).(f(x))在其任一周期内绝对可积
(2).(f(x))在其任一周期内只有有限个极值点
(3).(f(x))在任何有限区间内只能有有限个第一类间断点
其他判定条件
若函数(f(x))满足下列任一条件,则(f(x))的Fourier级数收敛到([f(x+0)+f(x-0)]/2).(充分非必要)
(1).$f(x) $分段连续,且每一点存在广义的左、右导数(分段可微)
(2).(f(x))分段单调(Dirichlet定理)
(3).在(x_0in[-pi,pi])处满足(alpha-{
m H{ddot o}lder})连续性,即(exists L>0,delta>0, {
m s.t. }forall tin U(x_0,delta), |f(x_0+t)-f(x_0) |le L|t|^{alpha})(Lipschitz定理)
在Fourier级数收敛的情况下,就可以将(f(x))写为:
[f(x)=frac {a_0}2+sum_{n=1}^{infty}(a_ncos(frac {2pi nx}{T})+b_nsin(frac{2pi nx}{T}))
]
Fourier变换(FT)
与Fourier级数不同,Fourier变换使得非周期函数也可以由三角级数逼近,这一点主要是通过将周期(T)从一有限数推广至无穷大来实现。
Fourier变换公式
[{mathcal F}[f(t)]=int _{-infty}^{+infty}f(t)e^{-jomega t}{
m d}t=int _{-infty}^{+infty}f(t)(cosomega t+jsin omega t) {
m d}t
]
逆变换
[f(t)=frac 12int_{-infty}^{+infty}{mathcal F}[f(t)]e^{jomega t}{
m d}omega
]
离散Fourier变换(DFT)
离散Fourier变换是应用于离散采样的时域信号的Fourier变换,对于有限时长,且具有(N)个样本数(采样间距相等)的离散时间信号(x(m)),其DFT形式如下定义:
[X(k)=sum_{m=0}^{N-1}x(m)e^{-jfrac{2pi}{N} mk},quad k=0,1,cdots,N-1
]
逆变换:
[x(m)=frac1Nsum_{k=0}^{N-1}X(k)e^{jfrac{2pi}{N} mk},quad m=0,1,cdots,N-1
]
离散余弦变换(DCT)
先看上边DFT的公式,将其展开成三角多项式形式
[�egin{aligned}
X(k)&=sum_{m=0}^{N-1}x(m)(cos(frac{2pi mk}{N})-jsin(frac{2pi mk}{N}))\
&=sum_{m=0}^{N-1}x(m)cos(frac{2pi mk}{N})-jsum_{m=0}^{N-1}x(m)sin(frac{2pi mk}{N})
\
quad (k&=0,1,cdots,N-1)
end{aligned}
]
显然DFT的结果中实部全部由余弦成分构成,虚部全部由正弦成分构成,即
实数部分:
[{
m Re}[X(k)]=sum_{m=0}^{N-1}x(m)cos(frac{2pi mk}{N})
]
虚数的系数部分:
[{
m Im}[X(k)]=sum_{m=0}^{N-1}x(m)sin(frac{2pi mk}{N})
]
显然({
m Re}[X(k)])是偶函数,而({
m Im}[X(k)])是奇函数。
接下来利用离散实信号({x(0),x(1),cdots,x(N-1) })来构造一个信号(x'(m)),定义如下:
[x'(m+frac 12)=
left{
�egin{array}{l}
x(m),quad 0le mle N-1\
x(-m-1),quad -Nle mle -1
end{array}
ight.
]
对于(0le mle N-1):
[x'(-(m+frac12))=x'(-m-frac12)=x'(-(m+1)+frac12)=x((m+1)-1)=x(m)=x'(m+frac12)
]
对于(-Nle mle -1):
[x'(m+frac12)=x(-m-1)=x'(-m-1+frac12)=x'(-(m+frac12))
]
于是(x'(m))是一个实偶信号,采样点也从({0,1,cdots,N-1})变为({-N+1/2,-N+3/2,cdots,1/2,cdots,N-1/2 }),如果写出(x'(m))的DFT公式,其形式为
[�egin{aligned}
X’(k)&=sum_{m=-N+frac12}^{N-frac12}x'(m)(cos(frac{2pi mk}{2N})-jsin(frac{2pi mk}{2N}))\
&=sum_{m=-N+frac12}^{N-frac12}x'(m)cos(frac{2pi mk}{2N})-jsum_{m=-N+frac12}^{N-frac12}x'(m)sin(frac{2pi mk}{2N})
\
end{aligned}
]
观察其虚部,由于虚部全部由正弦成分组成,为奇函数。奇函数乘以一个偶函数(x'(m))仍然是奇函数,而一个奇函数在关于零点对称的集合上对函数值求和等于零,又由其实部满足偶函数性质,所以(X'(k))可以进一步简化为
[�egin{aligned}X'(k)&=sum_{m=-N+frac12}^{N-frac12}x'(m)cos(frac{2pi mk}{2N})\&=2sum_{m=frac12}^{N-frac12}x'(m)cos(frac{2pi mk}{2N})\&=2sum_{n=0}^{N-1}x(n)cos(frac{kpi (n+frac12)}{N})end{aligned}
]
另如下定义(c(k))(为何这么定义?解释在这里)
[c(k)=left{ �egin{array}{l}frac 1 {sqrt N},quad k=0\sqrt{frac 2{N}},quad k=1,2,cdots,N-1end{array}
ight.
]
最终形式
[X(k)=c(k)sum_{n=0}^{N-1}x(n)cos(frac{kpi (n+frac12)}{N})
]
二维离散余弦变换(2D-DCT)
对(M imes N)矩阵([f(x,y)]),([f(x,y)])的DCT形式如下
[F(u,v)=c(u)c(v)sum_{x=0}^{M-1}sum_{y=0}^{N-1}f(x,y)cosfrac {(2x+1)upi}{2M}cosfrac {(2y+1)vpi}{2N}
]
(c(k))定义类似一维形式。特别地,当(M=N)时,2D-DCT可用矩阵乘法表示:
[F=A[f(x,y)]A^T
]
其中
[A=left [�egin{matrix}sqrt{1/N}[1 &1&1&cdots&1]\sqrt{2/N}[cos(pi/2N) &cos(3pi/2N) &cos(5pi/2N) &cdots&cos((2N-1)pi/2N)]\sqrt{2/N}[cos(2pi/2N) &cos(6pi/2N)&cos(10pi/2N)&cdots&cos(2(2N-1)pi/2N)]\vdots\sqrt{2/N}[cos((N-1)pi/2N) &cos(3(N-1)pi/2N)&cos(5(N-1)pi/2N)&cdots&cos((N-1)(2N-1)pi/2N)]\end{matrix}
ight]
]
