- 例如:p(x) = x3 - 3x+5
- 可以使用向量P=[1,0,-3,5]表示,向量长度减一表示多项式最高项次数。
- 从右到左分别是变量x的0次幂、1次幂、2次幂……n次幂。
- 这里可以使用numpy的方法ployval进行计算。
-
1 import numpy as np 2 p = np.array([1,0,-3,5]) 3 x=5 4 print(np.polyval(p,x)) 5 6 x = [1,2,3,4,5] 7 print(np.polyval(p,x))
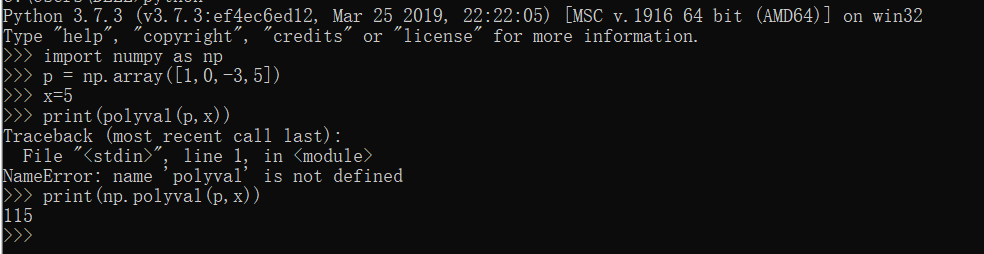
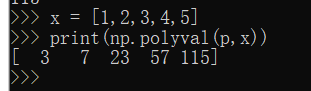
-
- 上图所示求出X为不同值时多项式的值,同样np内也有方法可以求出多项式的根。
-
import numpy as np p = np.array([1,0,-3,5]) b = np.roots(p) #求根 print(b) r = np.real(b) #取实数 print(r)
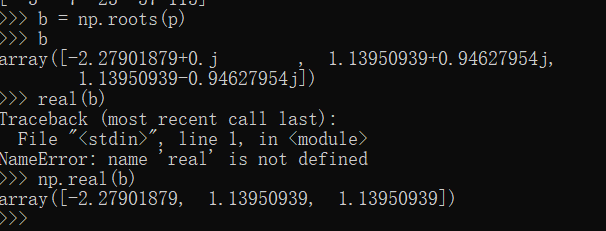
-
- 多项式乘法
- 在泛函分析中,卷积(convolution)是通过两个函数 f 和 g 生成第三个函数的一种数学算子,表示函数 f 经过翻转与平移与 g 的重叠部分的累积。
-
import numpy as np a = np.array([1,2,3,4]) b = np.array([1,4,9,16]) print(np.convolve(a,b))
即(x3+2x2+3x+4 )X (x3+4x2+9x+16) = [1,2,20,50,75,84,64]
-

-
- 在泛函分析中,卷积(convolution)是通过两个函数 f 和 g 生成第三个函数的一种数学算子,表示函数 f 经过翻转与平移与 g 的重叠部分的累积。
未完待续……