20172324 2018-2019-1《程序设计与数据结构》实验三报告

20172324 2018-2019-1《程序设计与数据结构》实验三报告

课程：《程序设计与数据结构》
班级： 1723
姓名： 曾程
学号：20172324
实验教师：王志强
实验日期：2018年11月19日
必修/选修： 必修

一、实验内容

链表练习

• 实验一：定义一个Searching和Sorting类，并在类中实现linearSearch（教材P162 ）,SelectionSort方法（P169），最后完成测试。

  1. 要求不少于10个测试用例，提交测试用例设计情况（正常，异常，边界，正序，逆序），用例数据中要包含自己学号的后四位提交运行结果图。

• 实验二：重构你的代码把Sorting.java Searching.java放入cn.edu.besti.cs1723.（姓名首字母+四位学号）包中（例如：cn.edu.besti.cs1723.G2301）把测试代码放test包中

  1. 重新编译，运行代码，提交编译，运行的截图（IDEA，命令行两种）

• 实验三：参考http://www.cnblogs.com/maybe2030/p/4715035.html 在Searching中补充查找算法并测试提交运行结果截图

• 实验四：补充实现课上讲过的排序方法：希尔排序，堆排序，二叉树排序等(至少3个)

  1. 测试实现的算法（正常，异常，边界）
     提交运行结果截图

• 实验五：编写Android程序对各种查找与排序算法进行测试
  提交运行结果截图3

二、实验过程及结果

• 实验1结果截图：

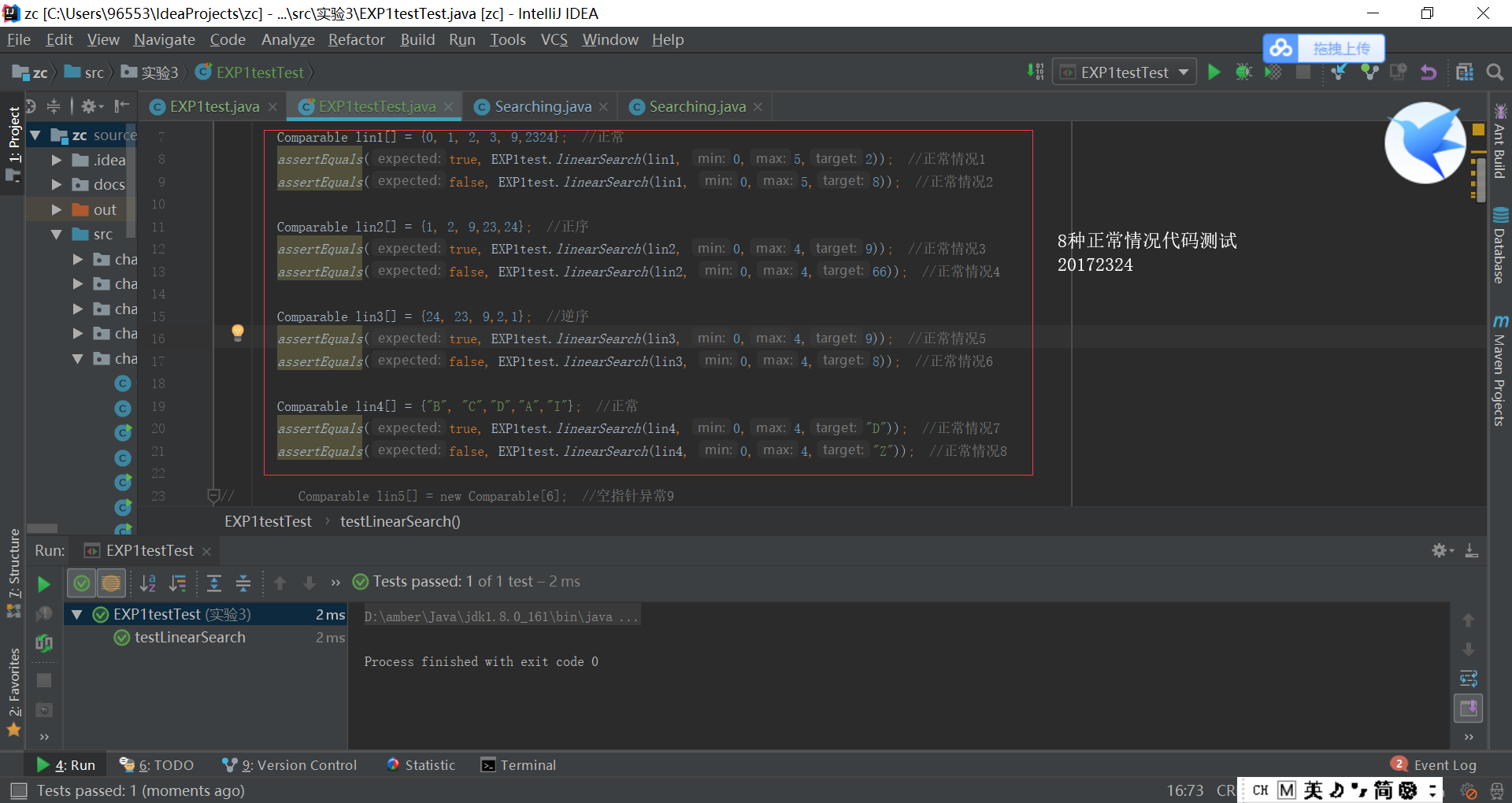
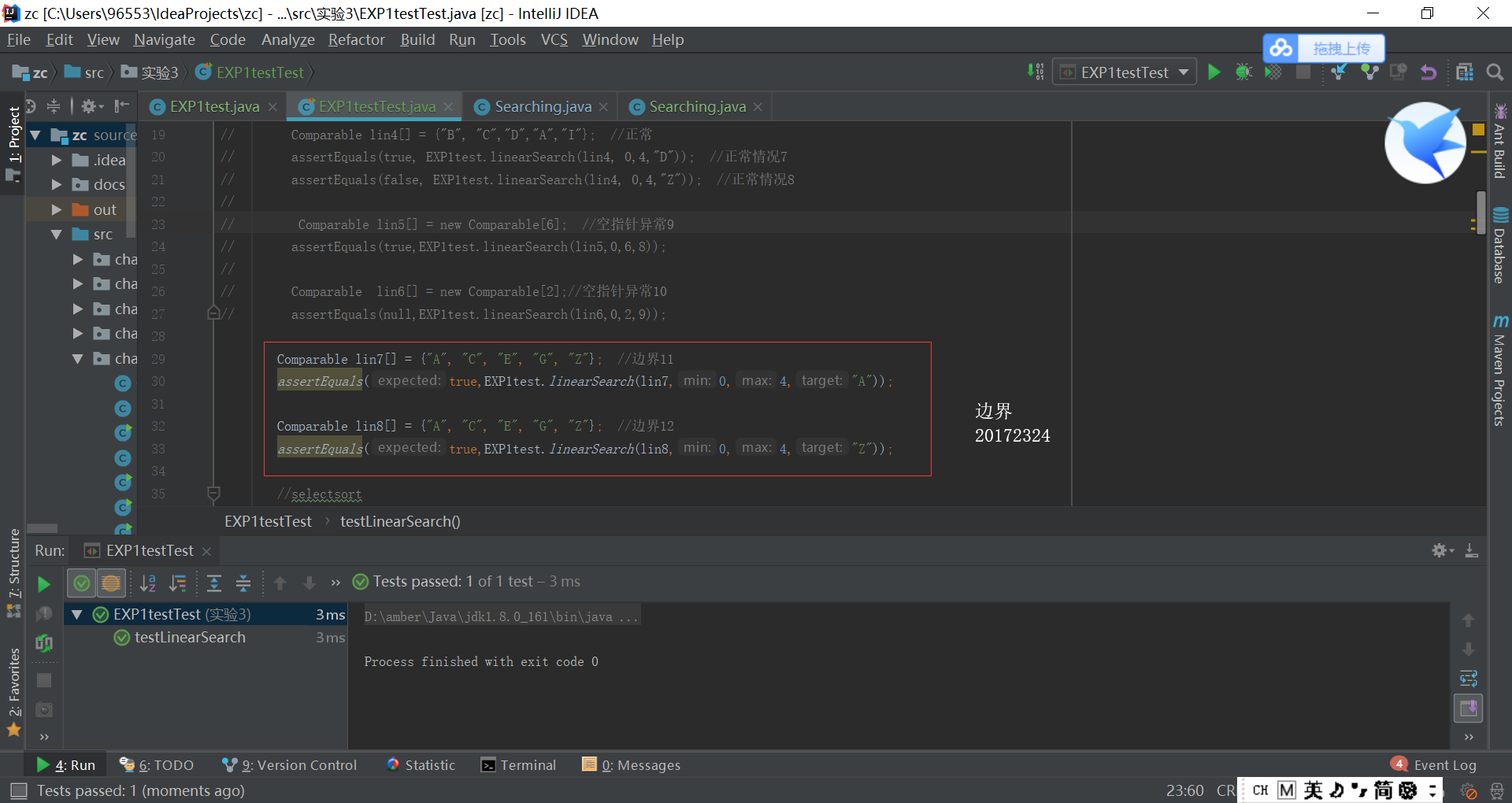
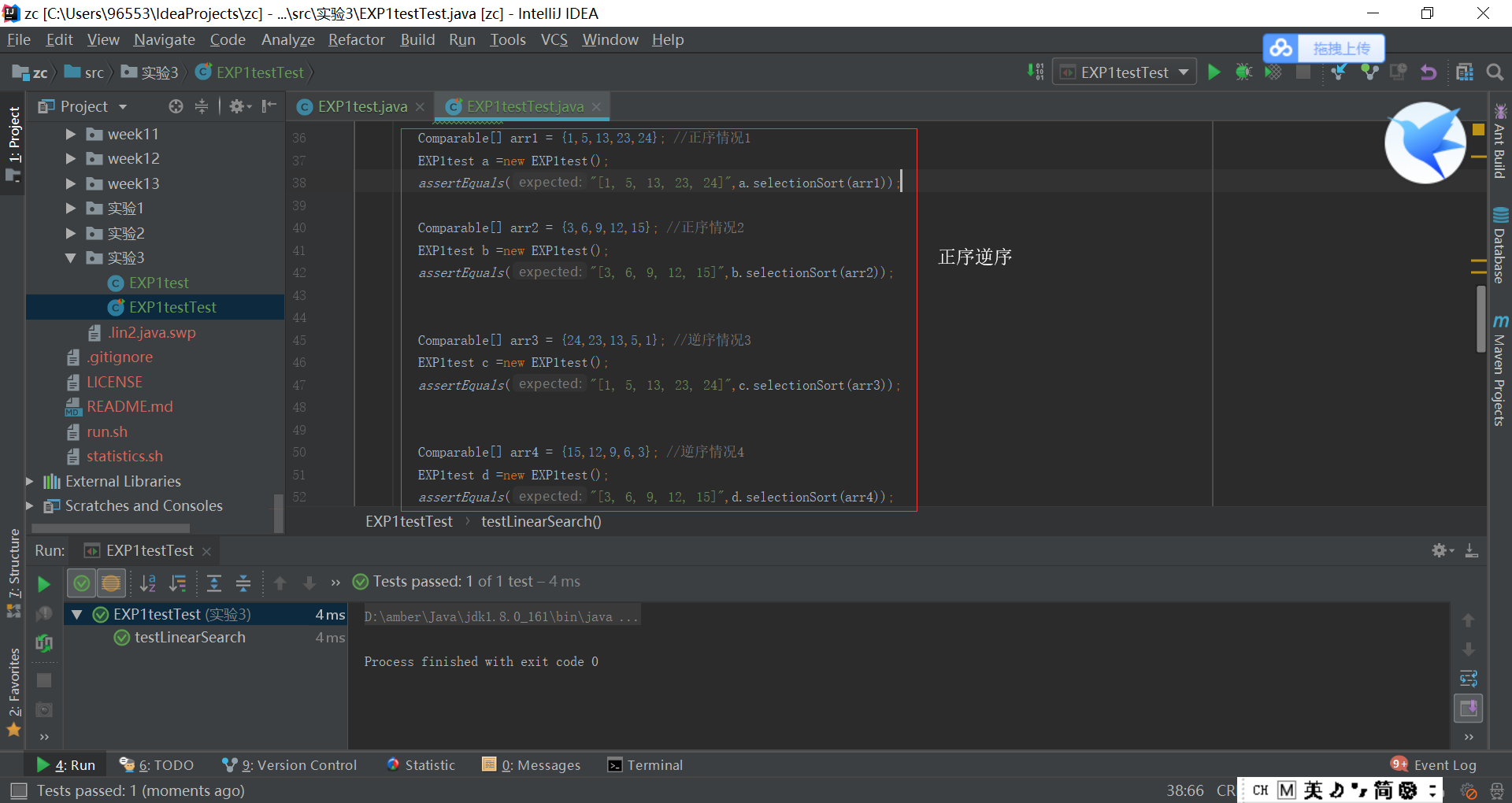
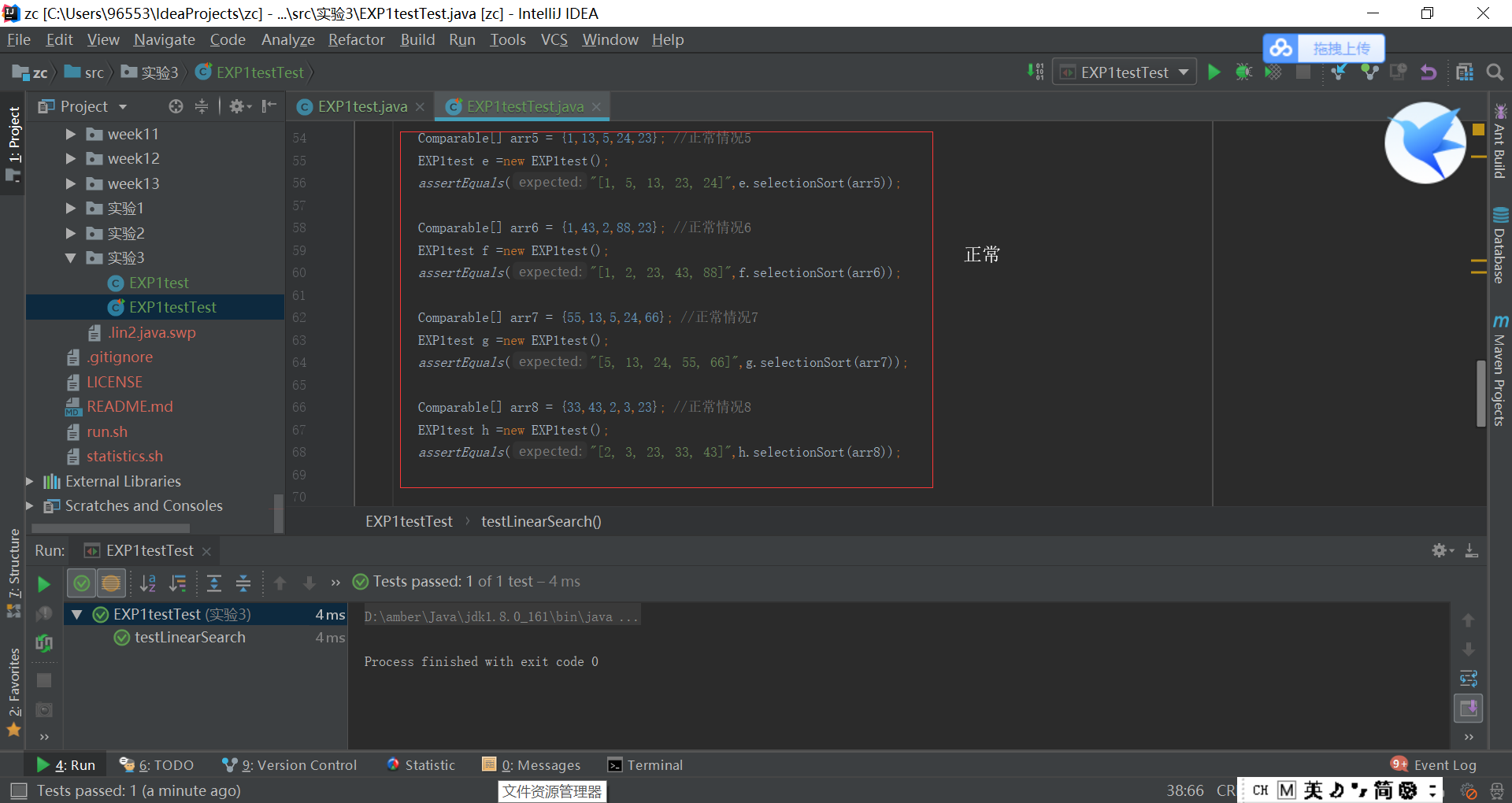
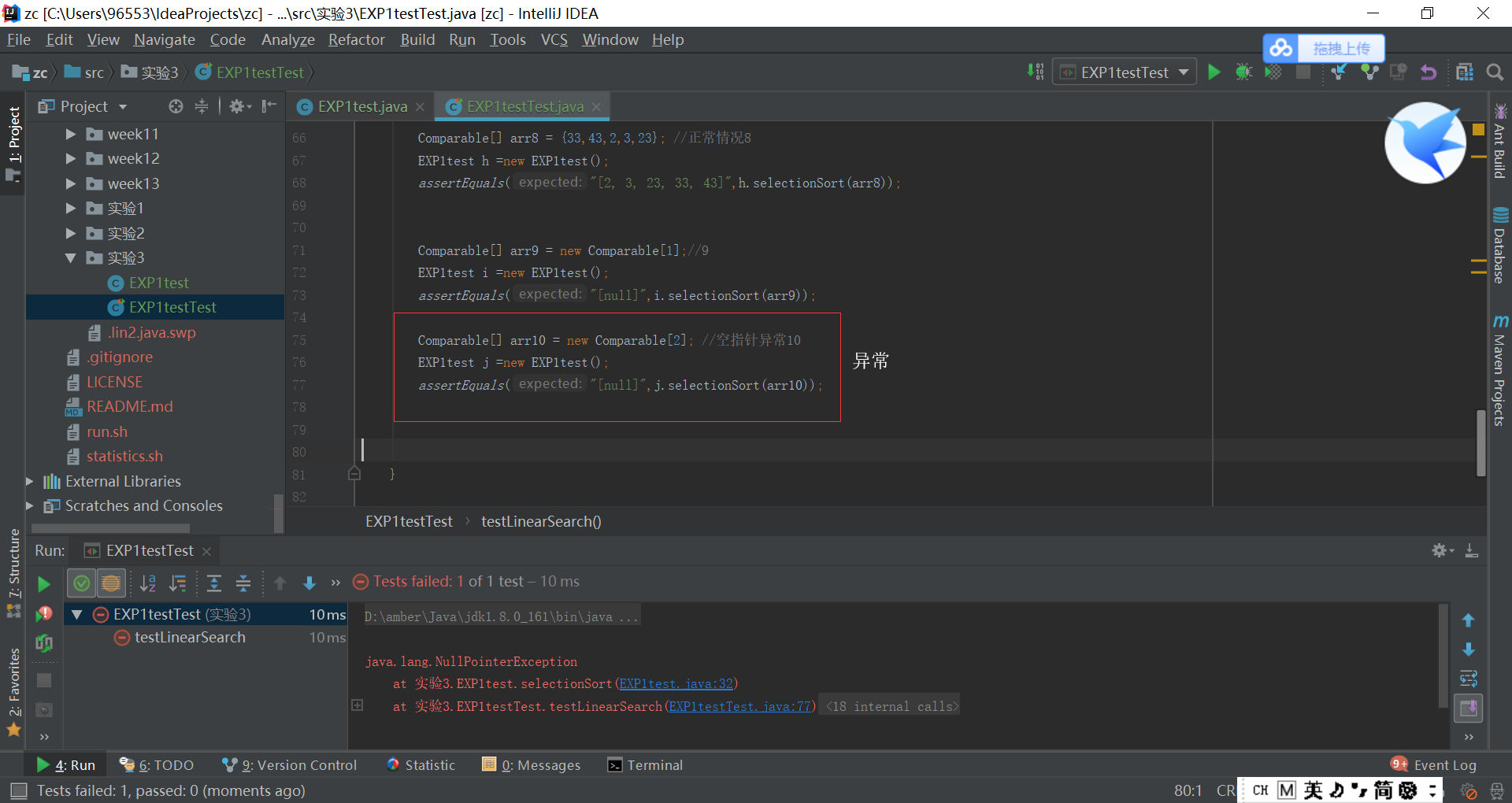
  • 定义Searching和Sorting类都已经在原来的代码里编写过了，唯一需要进行的就是测试代码，正常情况正序逆序都还比较容易理解，但是边界情况和异常情况不是很清楚，边界就是说如果给出{"A"、"B"、"C"、"D"、"E"}这一个数组，A和E就是边界；异常情况就是空指针等情况
    
    
    
    
    
    

• 实验2结果截图：

  • 在命令行中运行代码并完成编译
    
    

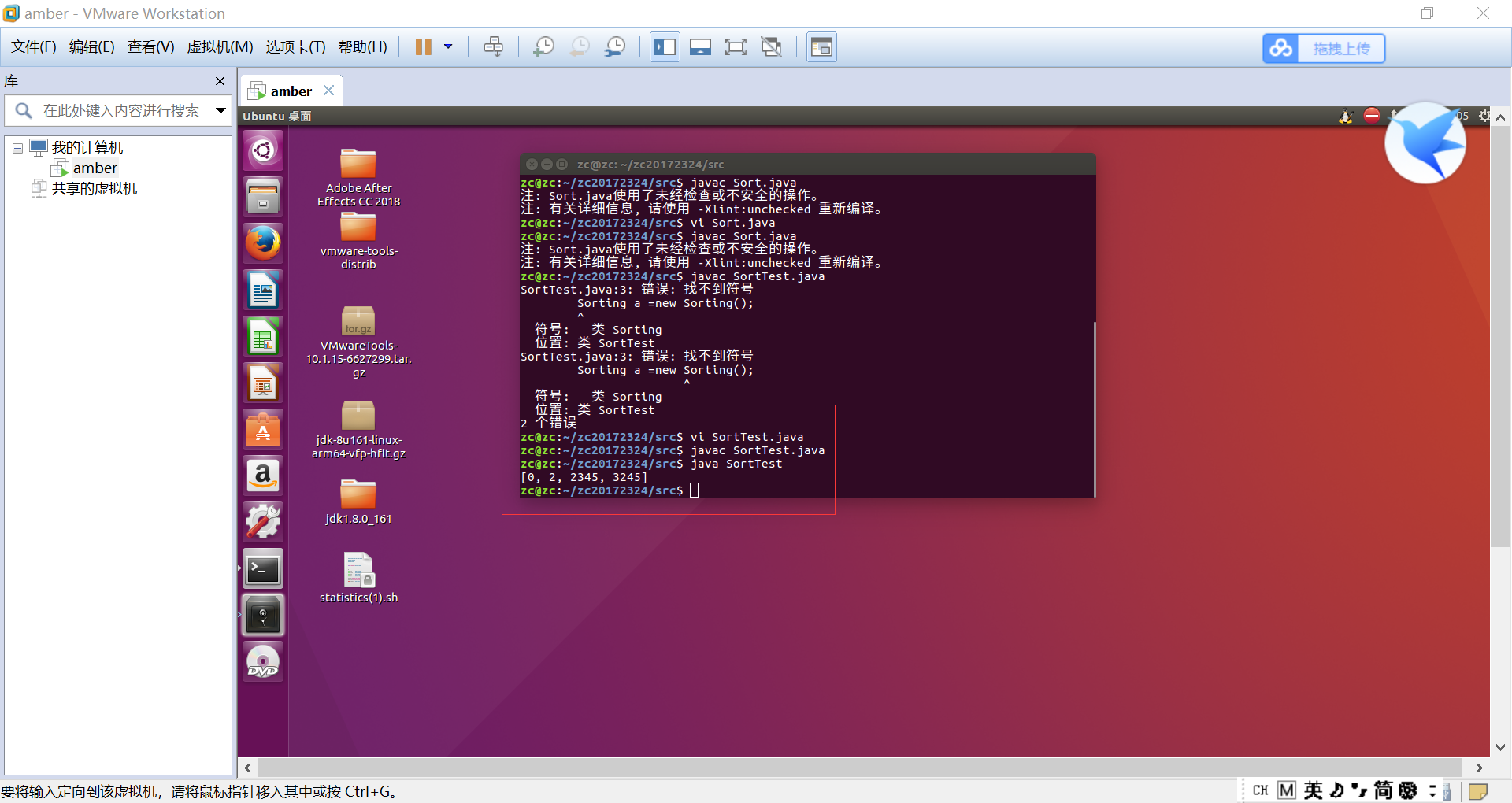
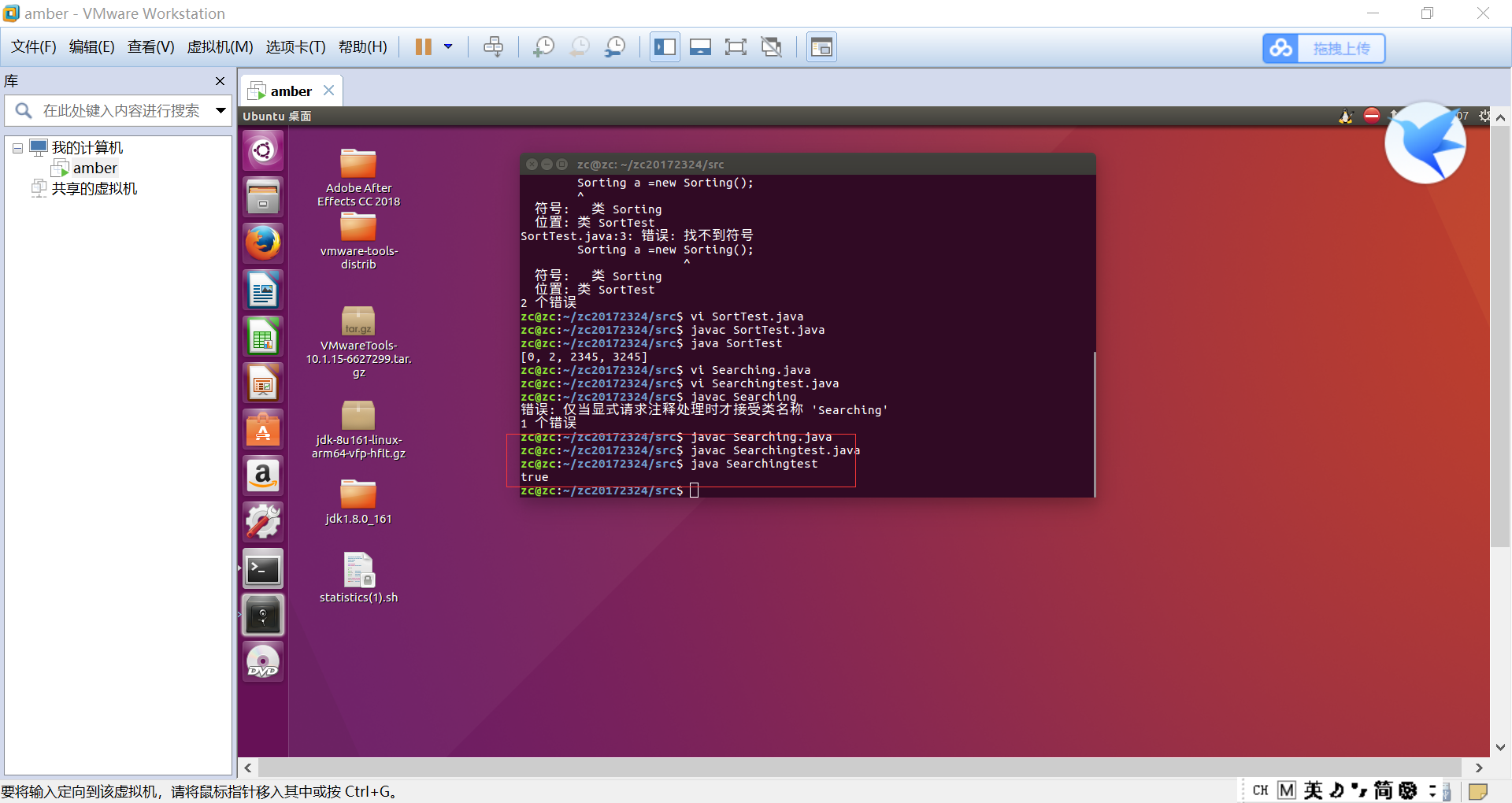
  • 将Sorting.java和Seaching.java放在另一个包里
    

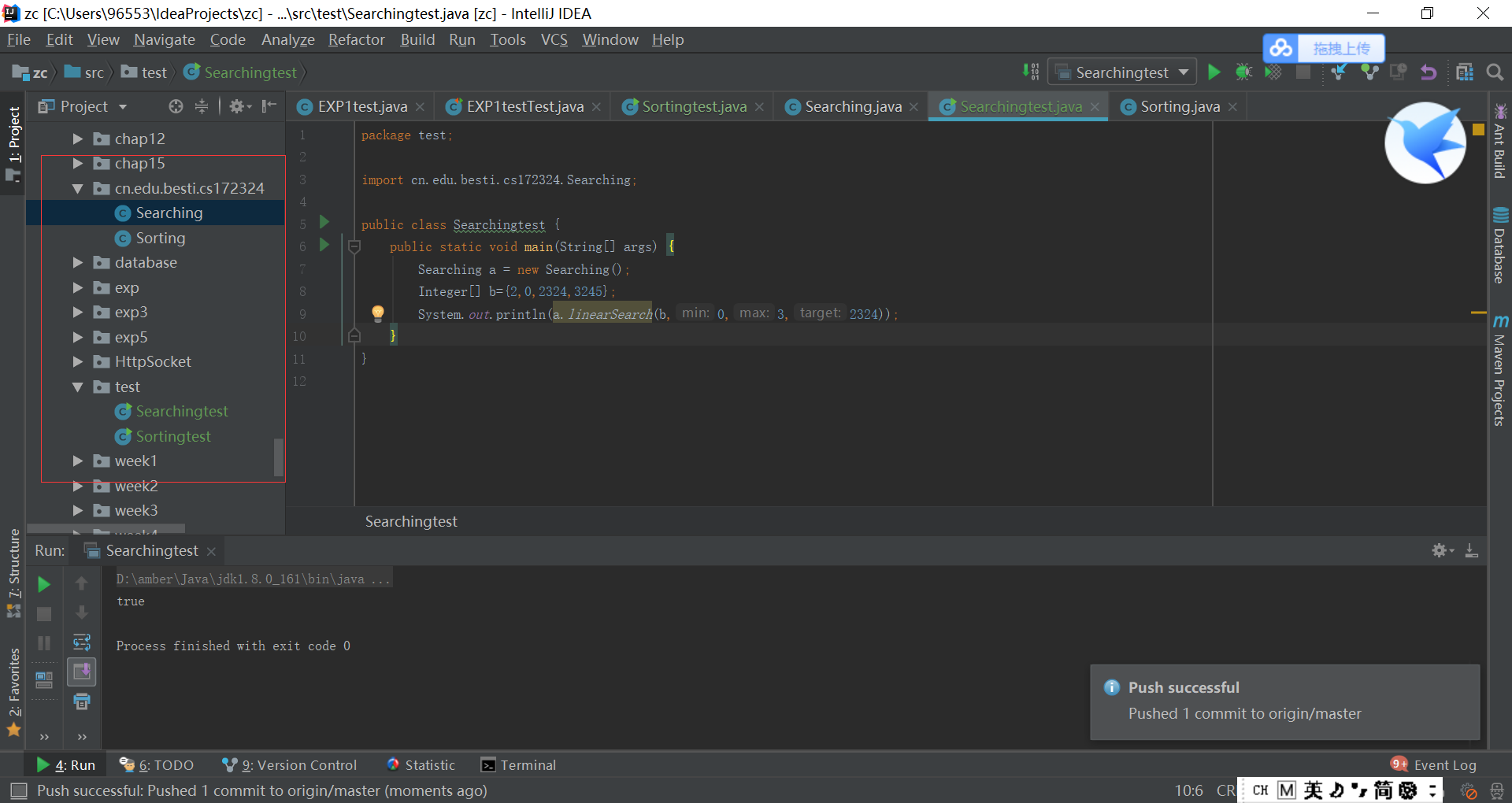
• 实验3结果截图：

  • 该实验需要补充的其实就是插值查找、斐波那契查找和分块查找
  • 对于有序列表，插值查找的平均性能更好。具体实现代码如下：

 public static int InsertionSearch(int[] a, int value, int low, int high) {
        int mid = low + (value - a[low]) / (a[high] - a[low]) * (high - low);
        if (a[mid] == value)
            return mid;
        if (a[mid] > value)
            return InsertionSearch(a, value, low, mid - 1);
        else
            return InsertionSearch(a, value, mid + 1, high);
    }

• 斐波那契数列，又称黄金分割数列，指的是这样一个数列：1、1、2、3、5、8、13、21、····，在数学上，斐波那契被递归方法如下定义：F(1)=1，F(2)=1，F(n)=f(n-1)+F(n-2) （n>=2）。该数列越往后相邻的两个数的比值越趋向于黄金比例值（0.618）。
  斐波那契查找就是在二分查找的基础上根据斐波那契数列进行分割的。在斐波那契数列找一个等于略大于查找表中元素个数的数F[n]，将原查找表扩展为长度为Fn，完成后进行斐波那契分割，即F[n]个元素分割为前半部分F[n-1]个元素，后半部分F[n-2]个元素，找出要查找的元素在那一部分并递归，直到找到。具体实现如下：

public static boolean FibonacciSearch(int[] table, int keyWord) {
        //确定需要的斐波那契数
        int i = 0;
        while (getFibonacci(i) - 1 == table.length) {
            i++;
        }
        //开始查找
        int low = 0;
        int height = table.length - 1;
        while (low <= height) {
            int mid = low + getFibonacci(i - 1);
            if (table[mid] == keyWord) {
                return true;
            } else if (table[mid] > keyWord) {
                height = mid - 1;
                i--;
            } else if (table[mid] < keyWord) {
                low = mid + 1;
                i -= 2;
            }
        }
        return false;
    }
    //得到第n个斐波那契数
    public static int getFibonacci(int n) {
        int res = 0;
        if (n == 0) {
            res = 0;
        } else if (n == 1) {
            res = 1;
        } else {
            int first = 0;
            int second = 1;
            for (int i = 2; i <= n; i++) {
                res = first + second;
                first = second;
                second = res;
            }
        }
        return res;
    }

• 实验4结果截图：

  • 这个实验上课的时候就实现过
    

• 实验5结果截图：
  

三、实验过程中遇到的问题和解决过程

• 问题一：做实验1的Sorting测试的时候出现了一个问题：

 Comparable[] arr9 = new Comparable[1];//9
        EXP1test i =new EXP1test();
        assertEquals("[null]",i.selectionSort(arr9));

可以运行

 Comparable[] arr10 = new Comparable[999]; //空指针异常10
        EXP1test j =new EXP1test();
        assertEquals("[null]",j.selectionSort(arr10));

不可以运行，为什么？

• 问题一解决方案：我当时做作业的时候是这样思考的：arr9和arr10应该都应该都是边界异常的情况，但是当我测试的时候我发现arr9可以运行但是arr10会报出边界异常的情况。开始我想的是也许是因为arr10中太大了，于是就把999换成了99，但是这样出来的结果仍然是边界异常，我问了王老师后王老师让我把数组的大小换成2，结果仍然是边界异常。解释就是当数组为1的时候，测试出来的就是[null]，已经异常了。当数组增加为2的时候测试出来是[null][null]。随着数组大小的增加，空数组的数量越来越多，太多的时候就显示不出来了。

四、代码链接

五、参考资料

• Java Collections API源码分析