主成分分析简介

本文主要介绍总体及样本的主成分的概念，如何可视化，以及一些最基本的性质。

1 总体的主成分

考虑\(x\sim (\mu,\Sigma)\)，其中\(\Sigma\)可分解为\(\Sigma=\Gamma\Lambda\Gamma'\)，\(\Gamma=(\eta_1,\ldots,\eta_d)\)，各列为单位特征向量，\(\Lambda\)为特征值降序排列的对角矩阵，协方差矩阵的秩\(\text{rank}(\Sigma)=r\)，对于\(k=1,\ldots,r\)，定义如下概念：

• 第\(k\)个principal component score（主成分得分）为\(w_k=\eta_k' (x-\mu)\)；
• 第\(k\)个principal component vector（主成分向量）为\(w^{(k)}=(w_1,\ldots,w_k)'=\Gamma_k' (x-\mu)\)；
• 第\(k\)个principal component projection (vector)（主成分映射（向量））为\(p_k=\eta_k\eta_k'(x-\mu)=w_k\eta_k\)。

我们来仔细看以上几个概念。\(\eta_k\)也叫载荷（loading），score \(x_k\)其实就是\(x\)在方向\(\eta_k\)上的贡献，也就是将\(x\)投影到\(\eta_k\)，而将前\(k\)个score放到一起，就组成了\(x^{(k)}\)。\(p_k\)是一个\(d\)维向量，它的方向就是\(\eta_k\)的方向，长度/欧式范数为\(\vert x_k\vert\)。

2 样本的主成分

假设我们有\(n\)个样本，将它们排成\(d\times n\)的矩阵\(X=(x_1,\ldots,x_n)\)，记样本均值\(\bar x=\dfrac{1}{n}X\ell_n\)，样本协方差矩阵\(S=\dfrac{1}{n-1}(X-\bar x \ell_n')(X-\bar x \ell_n')'\)，并且\(\text{rank}(S)=r\leq d\)。

我们可以对样本协方差矩阵进行谱分解\(S=\hat\Gamma \hat\Lambda \hat\Gamma'\)。与在总体中的定义一样，可以在样本中定义如下概念：

• 第\(k\)个principal component score为\(w_k=\hat\eta_k' (X-\bar x\ell_n')\)，这是一个\(1\times n\)的行向量；
• principal component data为\(W^{(k)}=(w_1',\ldots,w_k')'=\hat\Gamma_k' (X-\bar x\ell_n')\)，它是\(k\times n\)的矩阵；
• 第\(k\)个principal component projection为\(P_k=\hat\eta_k\hat\eta_k'(X-\bar x\ell_n')=\hat\eta_k w_k\)，它是\(d\times n\)的矩阵。

3 主成分的可视化

本节考察如何将PC的贡献、PC scores \(W^{(k)}\)、PC projection \(P_k\)进行可视化。

3.1 Scree plot

对于总体数据，\(\text{rank}(\Sigma)=r\)，我们定义第\(k\)个PC，对总体协方差的贡献为

\[\dfrac{\lambda_k}{\sum_{j=1}^{r}\lambda_j}=\dfrac{\lambda_k}{\text{tr}(\Sigma)} \]

再定义前\(\kappa\)个PC对总体协方差的累积贡献为

\[\dfrac{\sum_{k=1}^{\kappa}\lambda_k}{\sum_{j=1}^{r}\lambda_j}=\dfrac{\sum_{k=1}^{\kappa}\lambda_k}{\text{tr}(\Sigma)} \]

对于不同\(k\)画出前\(k\)个PC的贡献和累积贡献，就得到了scree plot，如下图：

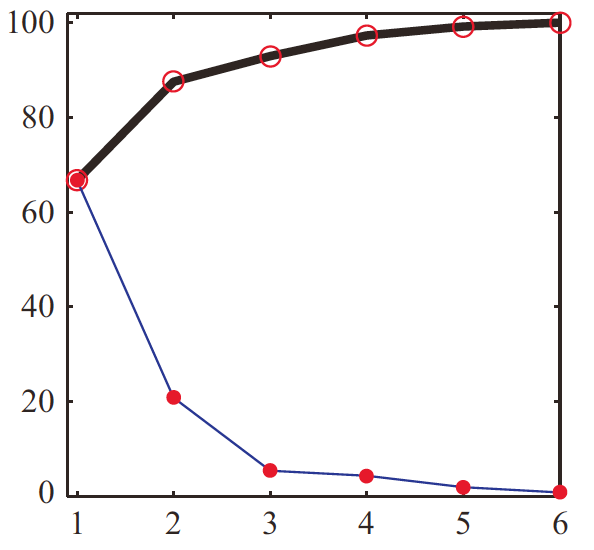
Scree plot中，有时可以找到elbow，传统方法是找出能比较好地代表数据的\(\kappa\)个点，就是elbow在的地方。有些文献中也叫knee或kink。在上图的例子中，elbow就是在第\(3\)个特征值处出现。当然，在很多情况下，也可能没有elbow。

3.2 PC score plot

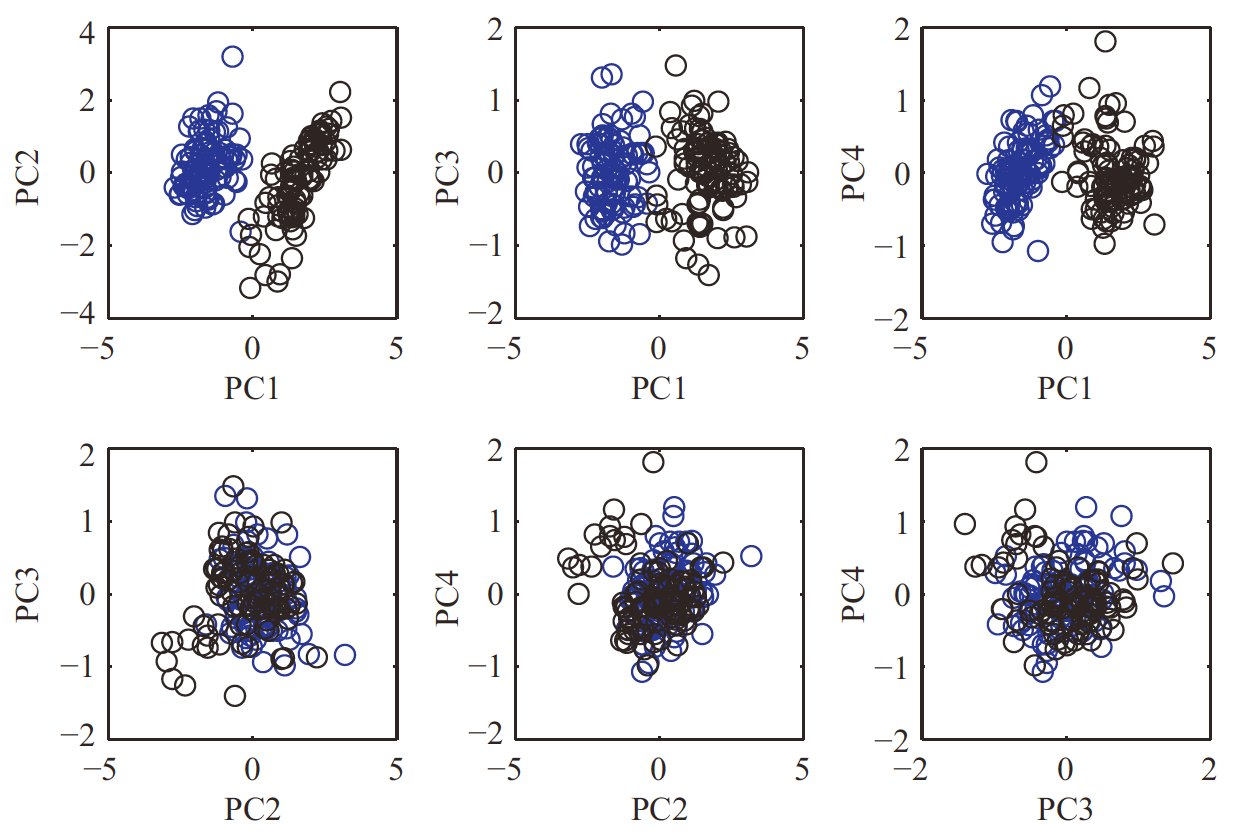
如果我们画出各PC的score，就叫PC score plot，但由于我们的视觉只能接受到三维的事物，因此对于超过三维，需要进行处理。比如对于\(W^{(4)}\)，我们可以成对地在二维平面上画出各PC的score，如下图：

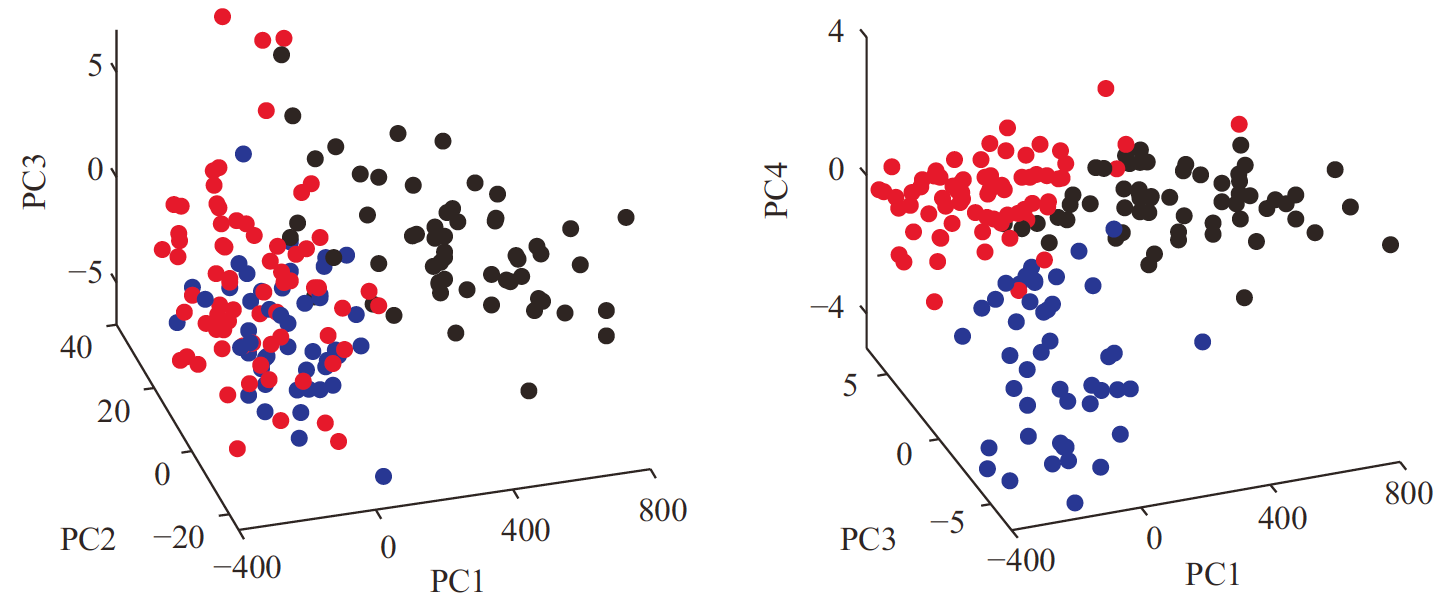
也可以直接画出三维图，如下图：

3.3 Projection plot

接下来看如何将\(P_k\)可视化。\(P_k\)为\(d\times n\)的矩阵，它的第\(i\)列就是第\(i\)个样本在\(\hat\eta_k\)方向的贡献。对于每个\(k\)，都可以用\(P_k\)画出平行坐标图，这样就很方便地将\(P_k\)可视化了。

第\(k\)个PC projection表示的其实就是用第\(k\)个score \(w_k\)对向量\(\hat\eta_k\)进行伸缩变换，因此也可以看一下这些score的分布，这就是密度估计（density estimates）。

下图是一个\(d=30\)的示例，左图为某个PC的projection plot，右图为非参数密度估计（可用Matlab工具curvdatSM）：

4 PC的性质

4.1 结构性质

本节考虑PC的一些性质，先看\(X\)和它的PC的相关结构。这里采用第1节的设定。

首先来看\(w^{(k)}=\Gamma_k' (x-\mu)\)，它的期望必满足\(\text{E}(w^{(k)})=0\)，这说明PC vectors都是中心化了的。而它的方差

\[\begin{aligned} \text{Var}(w^{(k)})=&\Gamma_k' \Sigma\Gamma_k\\ =&\Gamma_k' \Gamma\Lambda\Gamma'\Gamma_k\\ =&I_{k\times d}\Lambda I_{d\times k}\\ =&\Lambda_k \end{aligned} \]

即PC scores互不相关。当然，如果\(x\)是正态分布，那么PC scores也相互独立，否则需要用其他方法做出相互独立。

而\(w^{(k)}\)是由\(w_k=\eta_k' (x-\mu)\)作为元素组成的列向量，因此\(\text{Var}(w_k)=\lambda_k\)，\(\text{Cov}(w_k, w_l)=\eta_k'\Sigma\eta_l=\lambda_k\delta_{kl}\)，这里\(\delta_{kl}\)是Kronecker delta function（\(\delta_{kk}=1\)，对于\(k\neq l\)有\(\delta_{kl}=0\)）。由于\(\Lambda\)为按特征值降序排列的对角矩阵，因此必有

\[\text{Var}(w_1)\ge \text{Var}(w_2)\ge \cdots\ge \text{Var}(w_k) \]

对于\(\Sigma\)的特征值，有

\[\sum_{j=1}^{d}\lambda_j=\sum_{j=1}^{d}\sigma^2_j \]

其中\(\sigma_j^2\)为\(\Sigma\)的第\(j\)个对角线元素。这是因为\(\Sigma\)与\(\Lambda\)为相似矩阵，所以它们的迹一定相同。

如果用第2节中有关样本的设定，同样由于\(S=\hat\Gamma \hat\Lambda \hat\Gamma'\)，\(S\)与\(\hat\Lambda\)为相似矩阵，因此必有

\[\sum_{j=1}^{d} \hat\lambda_j = \sum_{j=1}^{d} s_j^2 \]

4.2 最优化性质

我们从另一个角度出发，来看主成分分析。

对于第1节中设定的总体\(x\)，假设\(\Sigma\)满秩，我们能不能找到一个\(d\)维的单位向量\(u\)，使得\(u'x\)的方差最大？

由于\(\Sigma\)满秩，那么它的\(d\)个特征向量可构成正交基，不妨设\(u=c_1 \eta_1+\cdots+c_d \eta_d\)，而\(u'u=1\)就等价于\(\sum_i c_i^2=1\)，则方差

\[\begin{aligned} \text{Var}(u'x) =& u'\Sigma u\\ =& \sum_{j,k} c_j c_k \eta_j'\Sigma\eta_k\\ =& \sum_{j,k} c_j c_k \lambda_k \eta_j'\eta_k\\ =& \sum_j c_j^2\lambda_j\\ \leq & \lambda_1 \sum_j c_j^2\\ =& \lambda_1 \end{aligned} \]

假设各特征值互不相同，那么上式只有当\(c_1^2=1\)且\(c_j=0\)（\(j\neq 1\)）时等号成立，此时\(u=\pm \eta_1\)。

接下来，我们寻找下一个\(u_2\)，要求\(u_2'x\)与\(\eta_1' x\)不相关，并能使\(u'x\)的方差最大。同样可设\(u_2=c_1 \eta_1+\cdots+c_d \eta_d\)，\(u_2'x\)与\(\eta_1' x\)不相关等价于\(u_2'\eta_1=0\)，此时又等价于\(c_1=0\)，重复上述过程，可以解出\(u_2'x\)的最大方差为\(\lambda_2\)，此时\(u_2=\pm \eta_2\)。

不断重复上述过程，可以找出\(d\)个\(u\)。

如果\(\text{rank}(\Sigma)=r\leq d\)，那么可找出\(r\)个特征值。如果特征值有重复，那么找出的\(u\)可能有多个解。