对【WMD： From Word Embedding to Document Distance】的理解

需改进：1. 增加实验结果 （7个SOTA)
2. 加速计算的逻辑 及 实验过程
3. WMD计算过程（尤其是代码部分cvxopt) 可以适当增加

零、背景简介

1. Word Embedding可有效表示不同词间的语义相似度（通常用欧式或余弦距离计算），词袋模型BOW(Bag of words)或TF-IDF更善于表示文档内的关键词，上述2种方法在表示不同文档间的语义相似性时就显得不那么好用了。因此作者提出基于Word Embedding的WMD(Word Mover's Distance)算法来计算文档间的距离（或语义相似性）
2. 该方法有效表示不同文档间的语义相似距离，算法无超参数且实现简单
3. WMD算法在找出一篇文档的k个最相似文档的错误率表现已超过目前最好的7个baseline

一、基本概念解释

1. 矩阵(X)是训练好的词库Embedding, d维，共n个单词

[X epsilon R^{ d imes n} ag 1 ]

2. (i^{th})表示词库中的第i个单词
3. (X_iepsilon R^d) 表示第i个单词（在词库中索引）的embedding表示，每个单词都是d维
4. (C_i)表示文档(d_i)中，第i个单词出现次数
5. (d_i) 即标准化词袋模型（nBOW),表示单词i出现在当前文档中的总次数 / 当前文档所有词出现总次数之和（当然要去除停用词），个人理解某篇文档d同理应该是n维的，要用词库及索引表示文档，因此会很稀疏，具体如下(2)式：

[d_i = frac {C_i}{sum_{j=1}^{n} C_j} ag 2 ]

6. (C(i,j))为文档1中第i个词到文档2中第j个词间Embedding的欧式距离，具体如下（3)式

[C(i，j） = left |left | X_i - X_j ight | ight |_2 ag 3 ]

7. (T_{i,j})同样为n*n矩阵，表示文档1中第i个单词到文档2中第j个单词间的转移成本（也可理解为权重向量），其中(T_{i,j})非负

二、WMD算法

1.算法思想

计算不同文档间的语义相似度（或距离），先用不同文档的所有单词（去除停用词）通过单词出现数量加权和标准化来向量化表示文档，再计算不同文档向量之间各个单词的映射关系，即找出文档1中所有单词分别映射到文档2中具体哪些单词（该步骤计算使用word embedding计算欧氏距离），最后对匹配好的所有单词距离进行计算并sum为文档距离。 该算法没有考虑文档中单词出现的顺序，考虑到了单词出现的数量，考虑了单词的语义相似性，也考虑了同一意思的不同句子可以用不同单词表示的情况。由于WMD算法时间复杂度较大，同时给出了2种优化算法。

2.目标函数

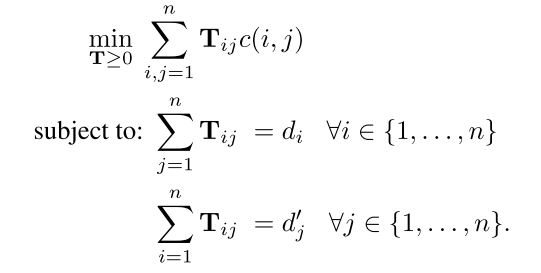
• 该目标函数表示计算文档1中的每一个单词i到文档2中的每一个单词的权重 和 embedding距离乘积的SUM， 其中有两个限制条件：

1. 文档1中第i个单词的权重(d_i)等于对应转移到文档2中的每个单词的权重和
2. 文档1中的每个单词的权重和等于转移到文档2中第j个单词的权重和(d'_j)

• 以上可表示为给定条件下的优化问题， 但平均时间复杂度是 (O(p^3log{p}))，p表示文档中去除停用词的单词unique数， 由于时间复杂度过高，原文给出了2中优化算法

三、优化算法

1.WCD（Word Centroid Distance)

该算法使用了初中数学讲的基本不等式性质：(left | a ight | + left | b ight | geqslant left | a+b ight |)，并分别对(T_{i,j})按行，列进行合并

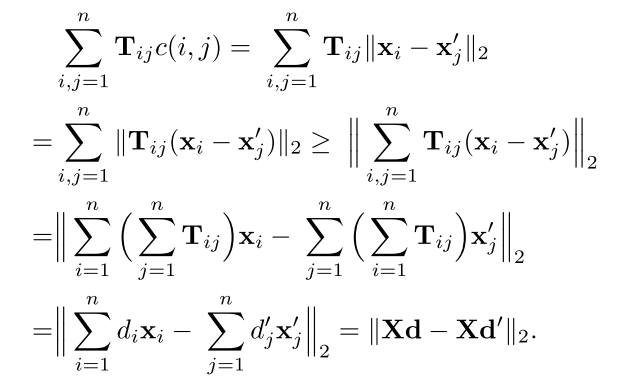
若用d表示单词embedding维度，p依然表示文档中去除停用词的单词unique数,则WCD的时间复杂度(O(dp)) ，极大的降低的时间复杂度，但是该算法计算的文档距离和WMD距离略远，可以作为WMD算法的下届（Lower Bound)

2. RWMD（Relaxed word moving distance)

该算法通过任意减少WMD算法的限制条件，降低了WMD的时间复杂度，并且RWMD结果更逼近WMD，如下图为RWMD目标函数

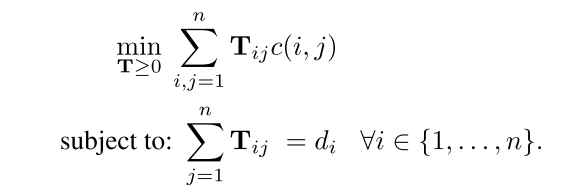
由于在计算(T_{i,j}^*)时使用了如下近似计算公式

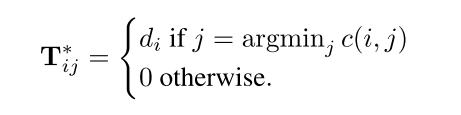
其近似优化结果如下图

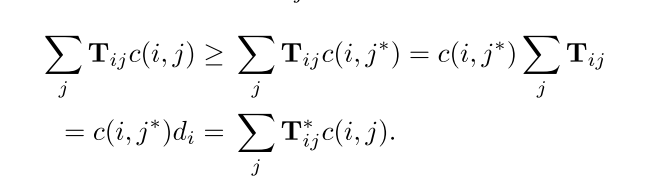
当分别去掉限制条件1和限制条件2时可获得文档距离分别为(l_1(d,d')) 和 (l_2(d,d')) ，而最终更逼近WMD的lower bound为(l_r(d,d') = max(l_1(d,d'),l_2(d,d')))，即RWMD计算结果。
该算法的时间夫再度是(O(P^2))

3. Prefetch and prune

根据以上两种近似算法，原文作者表示可以极大地降低计算量。若要使用WMD计算k篇最相近的文档，可以先用WCD计算得出前k语义最相似的文档，在对其余文档用RWMD算法计算，若后面计算的文档必前k个文档更相似（距离更小），那么再可用WMD算法计算该文档并更新前k个最相似文档，若使用RWMD计算的其余文档比之前WCD计算的文档距离更大，那么可剪枝跳过这些文档（因为它们一定是距离更远的）
以上方法是作者提出Prefetch and Prune剪枝操作，在某些数据集可减少95%的计算。

四、总结

1. WMD算法整体思路简单，无超参数，比BOW 和 TF-IDF 更能准确计算出文档语义相似度。
2. 2种优化算法，也较有效地提升了计算效率。
3. 展望:接下来若能考虑到句子中单词的顺序来计算语义相似度或能更好表示文档距离。