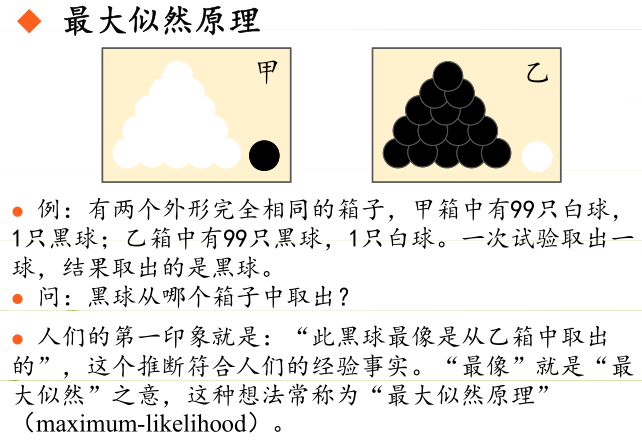
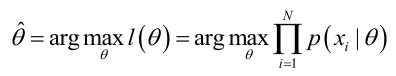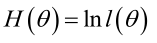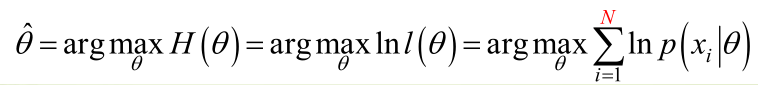一、定义
二、知识解读
极大似然估计，通俗理解来说，就是利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值！
换句话说，极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。
可能有小伙伴就要说了，还是有点抽象呀。我们这样想，一当模型满足某个分布，它的参数值我通过极大似然估计法求出来的话。比如正态分布中公式如下：
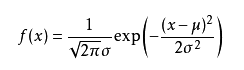
如果我通过极大似然估计，得到模型中参数和
的值，那么这个模型的均值和方差以及其它所有的信息我们是不是就知道了呢。确实是这样的。极大似然估计中采样需满足一个重要的假设，就是所有的采样都是独立同分布的。
下面我通过俩个例子来帮助理解一下最大似然估计
但是首先看一下似然函数 的理解：
对于这个函数： 输入有两个：x表示某一个具体的数据；
表示模型的参数
如果 是已知确定的，
是变量，这个函数叫做概率函数(probability function)，它描述对于不同的样本点
，其出现概率是多少。
如果 是已知确定的，
是变量，这个函数叫做似然函数(likelihood function), 它描述对于不同的模型参数，出现
这个样本点的概率是多少。
这有点像“一菜两吃”的意思。其实这样的形式我们以前也不是没遇到过。例如， , 即x的y次方。如果x是已知确定的(例如x=2)，这就是
, 这是指数函数。 如果y是已知确定的(例如y=2)，这就是
，这是二次函数。同一个数学形式，从不同的变量角度观察，可以有不同的名字。
这么说应该清楚了吧？ 如果还没讲清楚，别急，下文会有具体例子。
现在真要先讲讲MLE了。。
例子一
别人博客的一个例子。
假如有一个罐子，里面有黑白两种颜色的球，数目多少不知，两种颜色的比例也不知。我 们想知道罐中白球和黑球的比例，但我们不能把罐中的球全部拿出来数。现在我们可以每次任意从已经摇匀的罐中拿一个球出来，记录球的颜色，然后把拿出来的球 再放回罐中。这个过程可以重复，我们可以用记录的球的颜色来估计罐中黑白球的比例。假如在前面的一百次重复记录中，有七十次是白球，请问罐中白球所占的比例最有可能是多少？
很多人马上就有答案了：70%。而其后的理论支撑是什么呢？
我们假设罐中白球的比例是p，那么黑球的比例就是1-p。因为每抽一个球出来，在记录颜色之后，我们把抽出的球放回了罐中并摇匀，所以每次抽出来的球的颜 色服从同一独立分布。
这里我们把一次抽出来球的颜色称为一次抽样。题目中在一百次抽样中，七十次是白球的,三十次为黑球事件的概率是P(样本结果|Model)。
如果第一次抽象的结果记为x1,第二次抽样的结果记为x2....那么样本结果为(x1,x2.....,x100)。这样，我们可以得到如下表达式：
P(样本结果|Model)
= P(x1,x2,…,x100|Model)
= P(x1|Mel)P(x2|M)…P(x100|M)
= p^70(1-p)^30.
好的，我们已经有了观察样本结果出现的概率表达式了。那么我们要求的模型的参数，也就是求的式中的p。
那么我们怎么来求这个p呢？
不同的p，直接导致P（样本结果|Model）的不同。
好的，我们的p实际上是有无数多种分布的。如下：
那么求出 p^70(1-p)^30为 7.8 * 10^(-31)
p的分布也可以是如下：
那么也可以求出p^70(1-p)^30为2.95* 10^(-27)
那么问题来了，既然有无数种分布可以选择，极大似然估计应该按照什么原则去选取这个分布呢？
答：采取的方法是让这个样本结果出现的可能性最大，也就是使得p^70(1-p)^30值最大，那么我们就可以看成是p的方程，求导即可！
那么既然事情已经发生了，为什么不让这个出现的结果的可能性最大呢？这也就是最大似然估计的核心。
我们想办法让观察样本出现的概率最大，转换为数学问题就是使得：
p^70(1-p)^30最大，这太简单了，未知数只有一个p，我们令其导数为0，即可求出p为70%，与我们一开始认为的70%是一致的。其中蕴含着我们的数学思想在里面。
使用matlab查看其最大值
clear clc x = 0:0.1:1; y = (x.^70).*((1-x).^30); plot(x,y)
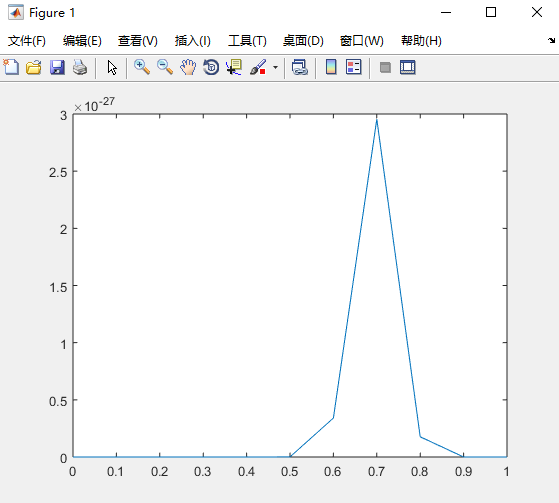
例子二
假设我们要统计全国人民的年均收入，首先假设这个收入服从服从正态分布，但是该分布的均值与方差未知。我们没有人力与物力去统计全国每个人的收入。我们国家有10几亿人口呢？那么岂不是没有办法了？
不不不，有了极大似然估计之后，我们可以采用嘛！我们比如选取一个城市，或者一个乡镇的人口收入，作为我们的观察样本结果。然后通过最大似然估计来获取上述假设中的正态分布的参数。
有了参数的结果后，我们就可以知道该正态分布的期望和方差了。也就是我们通过了一个小样本的采样，反过来知道了全国人民年收入的一系列重要的数学指标量！
那么我们就知道了极大似然估计的核心关键就是对于一些情况，样本太多，无法得出分布的参数值，可以采样小样本后，利用极大似然估计获取假设中分布的参数值。
例子三
三、求解过程
由于样本集中的样本都是独立同分布，可以只考虑一类样本集D，来估计参数向量θ。记已知的样本集为：
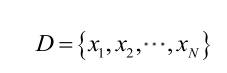
似然函数（linkehood function）：联合概率密度函数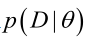
称为相对于
的θ的似然函数。
如果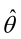
是参数空间中能使似然函数
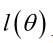最大的θ值，则
应该是“最可能”的参数值，那么
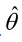就是θ的极大似然估计量。它是样本集的函数，记作：
求解极大似然函数
ML估计：求使得出现该组样本的概率最大的θ值。
实际中为了便于分析，定义了对数似然函数：
1. 未知参数只有一个（θ为标量）
在似然函数满足连续、可微的正则条件下，极大似然估计量是下面微分方程的解：
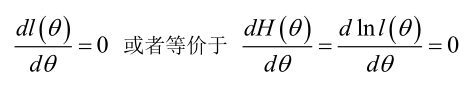
2.未知参数有多个（θ为向量）
则θ可表示为具有S个分量的未知向量：
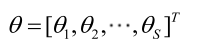
记梯度算子：
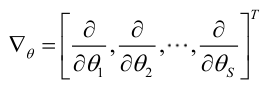
若似然函数满足连续可导的条件，则最大似然估计量就是如下方程的解。
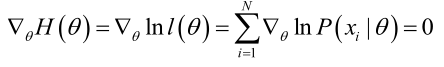
方程的解只是一个估计值，只有在样本数趋于无限多的时候，它才会接近于真实值。
极大似然估计的例子
例1：设样本服从正态分布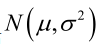
，则似然函数为：
它的对数：
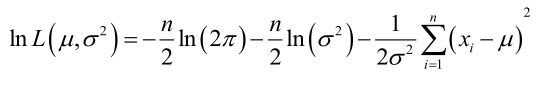
求导，得方程组：
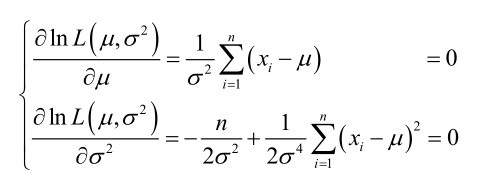
联合解得：
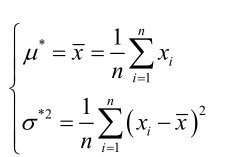
似然方程有唯一解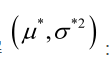
，而且它一定是最大值点，这是因为当
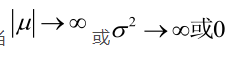时，非负函数
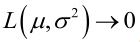。于是U和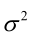
的极大似然估计为
。
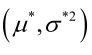例2：设样本服从均匀分布[a, b]。则X的概率密度函数：
对样本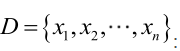
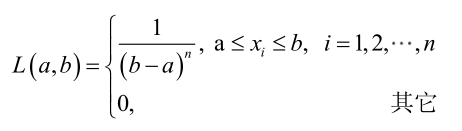
很显然，L(a,b)作为a和b的二元函数是不连续的，这时不能用导数来求解。而必须从极大似然估计的定义出发，求L(a,b)的最大值，为使L(a,b)达到最大，b-a应该尽可能地小，但b又不能小于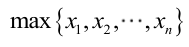
，否则，L(a,b)=0。类似地a不能大过
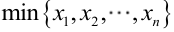，因此，a和b的极大似然估计：
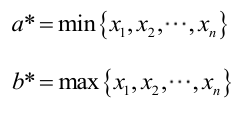
总结
求最大似然估计量的一般步骤：
（1）写出似然函数；
（2）对似然函数取对数，并整理；
（3）求导数；
（4）解似然方程。
最大似然估计的特点：
1.比其他估计方法更加简单；
2.收敛性：无偏或者渐近无偏，当样本数目增加时，收敛性质会更好；
3.如果假设的类条件概率模型正确，则通常能获得较好的结果。但如果假设模型出现偏差，将导致非常差的估计结果。
Matlab实例
实例一
x=[1.2 3.5 4.2 0.8 1.4 3.1 4.8 0.9]; u=mle(x)
实例二
下面用MATLAB实现正态分布的ML估计
% 二维正态分布的两分类问题 （ML估计）
clc;
clear;
% 两个类别数据的均值向量
Mu = [0 0; 3 3]';
% 协方差矩阵
S1 = 0.8 * eye(2);
S(:, :, 1) = S1;
S(:, :, 2) = S1;
% 先验概率（类别分布）
P = [1/3 2/3]';
% 样本数据规模
% 收敛性：无偏或者渐进无偏，当样本数目增加时，收敛性质会更好
N = 500;
% 1.生成训练和测试数据
%{
生成训练样本
N = 500, c = 2, d = 2
μ1=[0, 0]' μ2=[3, 3]'
S1=S2=[0.8, 0; 0.8, 0]
p(w1)=1/3 p(w2)=2/3
%}
randn('seed', 0);
[X_train, Y_train] = generate_gauss_classes(Mu, S, P, N);
figure();
hold on;
class1_data = X_train(:, Y_train==1);
class2_data = X_train(:, Y_train==2);
plot(class1_data(1, :), class1_data(2, :), 'r.');
plot(class2_data(1, :), class2_data(2, :), 'g.');
grid on;
title('训练样本');
xlabel('N=500');
%{
用同样的方法生成测试样本
N = 500, c = 2, d = 2
μ1=[0, 0]' μ2=[3, 3]'
S1=S2=[0.8, 0; 0.8, 0]
p(w1)=1/3 p(w2)=2/3
%}
randn('seed', 100);
[X_test, Y_test] = generate_gauss_classes(Mu, S, P, N);
figure();
hold on;
test1_data = X_test(:, Y_test==1);
test2_data = X_test(:, Y_test==2);
plot(test1_data(1, :), test1_data(2, :), 'r.');
plot(test2_data(1, :), test2_data(2, :), 'g.');
grid on;
title('测试样本');
xlabel('N=500');
% 2.用训练样本采用ML方法估计参数
% 各类样本只包含本类分布的信息，也就是说不同类别的参数在函数上是独立的
[mu1_hat, s1_hat] = gaussian_ML_estimate(class1_data);
[mu2_hat, s2_hat] = gaussian_ML_estimate(class2_data);
mu_hat = [mu1_hat, mu2_hat];
s_hat = (1/2) * (s1_hat + s2_hat);
% 3.用测试样本和估计出的参数进行分类
% 使用欧式距离进行分类
z_euclidean = euclidean_classifier(mu_hat, X_test);
% 使用贝叶斯方法进行分类
z_bayesian = bayes_classifier(Mu, S, P, X_test);
% 4.计算不同方法分类的误差
err_euclidean = ( 1-length(find(Y_test == z_euclidean')) / length(Y_test) );
err_bayesian = ( 1-length(find(Y_test == z_bayesian')) / length(Y_test) );
% 输出信息
disp(['基于欧式距离分类的误分率：', num2str(err_euclidean)]);
disp(['基于最小错误率贝叶斯分类的误分率：', num2str(err_bayesian)]);
% 画图展示
figure();
hold on;
z_euclidean = transpose(z_euclidean);
o = 1;
q = 1;
for i = 1:size(X_test, 2)
if Y_test(i) ~= z_euclidean(i)
plot(X_test(1,i), X_test(2,i), 'bo');
elseif z_euclidean(i)==1
euclidean_classifier_results1(:, o) = X_test(:, i);
o = o+1;
elseif z_euclidean(i)==2
euclidean_classifier_results2(:, q) = X_test(:, i);
q = q+1;
end
end
plot(euclidean_classifier_results1(1, :), euclidean_classifier_results1(2, :), 'r.');
plot(euclidean_classifier_results2(1, :), euclidean_classifier_results2(2, :), 'g.');
title(['基于欧式距离分类，误分率为：', num2str(err_euclidean)]);
grid on;
figure();
hold on;
z_bayesian = transpose(z_bayesian);
o = 1;
q = 1;
for i = 1:size(X_test, 2)
if Y_test(i) ~= z_bayesian(i)
plot(X_test(1,i), X_test(2,i), 'bo');
elseif z_bayesian(i)==1
bayesian_classifier_results1(:, o) = X_test(:, i);
o = o+1;
elseif z_bayesian(i)==2
bayesian_classifier_results2(:, q) = X_test(:, i);
q = q+1;
end
end
plot(bayesian_classifier_results1(1, :), bayesian_classifier_results1(2, :), 'r.');
plot(bayesian_classifier_results2(1, :), bayesian_classifier_results2(2, :), 'g.');
title(['基于最小错误率的贝叶斯决策分类，误分率为：', num2str(err_bayesian)]);
grid on;
生成数据的函数：
function [ data, C ] = generate_gauss_classes( M, S, P, N )
%{
函数功能：
生成样本数据，符合正态分布
参数说明：
M：数据的均值向量
S：数据的协方差矩阵
P：各类样本的先验概率，即类别分布
N：样本规模
函数返回
data：样本数据（2*N维矩阵）
C：样本数据的类别信息
%}
[~, c] = size(M);
data = [];
C = [];
for j = 1:c
% z = mvnrnd(mu,sigma,n);
% 产生多维正态随机数，mu为期望向量，sigma为协方差矩阵，n为规模。
% fix 函数向零方向取整
t = mvnrnd(M(:,j), S(:,:,j), fix(P(j)*N))';
data = [data t];
C = [C ones(1, fix(P(j) * N)) * j];
end
end
正态分布的ML估计（对训练样本）：
function [ m_hat, s_hat ] = gaussian_ML_estimate( X )
%{
函数功能：
样本正态分布的最大似然估计
参数说明：
X：训练样本
函数返回：
m_hat：样本由极大似然估计得出的正态分布参数，均值
s_hat：样本由极大似然估计得出的正态分布参数，方差
%}
% 样本规模
[~, N] = size(X);
% 正态分布样本总体的未知均值μ的极大似然估计就是训练样本的算术平均
m_hat = (1/N) * sum(transpose(X))';
% 正态分布中的协方差阵Σ的最大似然估计量等于N个矩阵的算术平均值
s_hat = zeros(1);
for k = 1:N
s_hat = s_hat + (X(:, k)-m_hat) * (X(:, k)-m_hat)';
end
s_hat = (1/N)*s_hat;
end
有了估计参数，对测试数据进行分类：
基于欧式距离的分类：
function [ z ] = euclidean_classifier( m, X )
%{
函数功能：
利用欧式距离对测试数据进行分类
参数说明：
m：数据的均值，由ML对训练数据，参数估计得到
X：我们需要测试的数据
函数返回：
z：数据所属的分类
%}
[~, c] = size(m);
[~, n] = size(X);
z = zeros(n, 1);
de = zeros(c, 1);
for i = 1:n
for j = 1:c
de(j) = sqrt( (X(:,i)-m(:,j))' * (X(:,i)-m(:,j)) );
end
[~, z(i)] = min(de);
end
end
基于最小错误率的贝叶斯估计：
function [ z ] = euclidean_classifier( m, X )
%{
函数功能：
利用欧式距离对测试数据进行分类
参数说明：
m：数据的均值，由ML对训练数据，参数估计得到
X：我们需要测试的数据
函数返回：
z：数据所属的分类
%}
[~, c] = size(m);
[~, n] = size(X);
z = zeros(n, 1);
de = zeros(c, 1);
for i = 1:n
for j = 1:c
de(j) = sqrt( (X(:,i)-m(:,j))' * (X(:,i)-m(:,j)) );
end
[~, z(i)] = min(de);
end
end
基于最小错误率的贝叶斯估计：
function [ z ] = bayes_classifier( m, S, P, X )
%{
函数功能：
利用基于最小错误率的贝叶斯对测试数据进行分类
参数说明：
m：数据的均值
S：数据的协方差
P：数据类别分布概率
X：我们需要测试的数据
函数返回：
z：数据所属的分类
%}
[~, c] = size(m);
[~, n] = size(X);
z = zeros(n, 1);
t = zeros(c, 1);
for i = 1:n
for j = 1:c
t(j) = P(j) * comp_gauss_dens_val( m(:,j), S(:,:,j), X(:,i) );
end
[~, z(i)] = max(t);
end
end
function [ z ] = comp_gauss_dens_val( m, s, x )
%{
函数功能：
计算高斯分布N（m, s），在某一个特定点的值
参数说明：
m：数据的均值
s：数据的协方差
x：我们需要计算的数据点
函数返回：
z：高斯分布在x出的值
%}
z = ( 1/( (2*pi)^(1/2)*det(s)^0.5 ) ) * exp( -0.5*(x-m)'*inv(s)*(x-m) );
end