题目链接
分析
这道题应该都能想到缩点+LCA吧,所以其实最难的问题是把它写出来
调了一天的我对此很无奈。
首先是缩边双还是缩点双,显然是点双,感性的说,求必须经过的点,所以就缩点双。理性一点呢?理性的说,必须经过的点就是割点,所以把点双缩在一起,注意一个问题,因为求的是割点,所以不要把割点也缩到点双里边。
缩完点后,形成的树可能有重边,但它看起来的确是树,一定是一个割点和点双一个接着一个的,所以求出路径长除以二下取整就行。
易错
- 给定的询问是边号,如果边在点双里,十分好处理,如果连接一个割点和一个点双呢?就需要把这条边映射到点双上而不是割点,因为emmm,大概就是这么一个图。
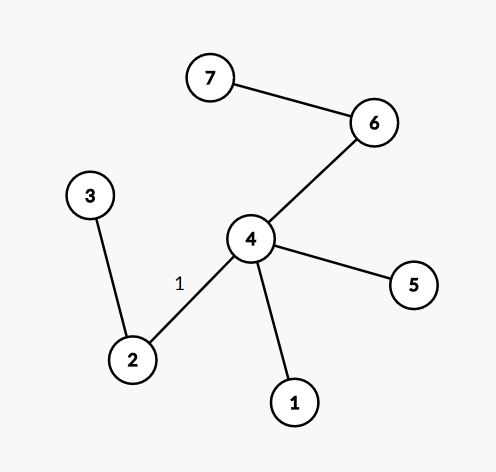
只要从1号边开始,到的不是4的邻接边,就一定会有一个割点,所以把边映射到点双上可以。 - 还是不要在tarjan里边缩点了,因为这个题比较复杂,涉及到割点的重新编号,你说它是一个圆方树吧,它又没方点,你说它不是吧,又挺像,反正我在tarjan里边缩点后,在某OJ上AC了,但是在HDU上WA了很多次,所以就直接在外边缩吧,还省点脑子。
- 实在调不出来就重新写吧
还有些注释都写代码里了
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=2e5+10;
struct Edge{
int to,nxt;
}E[N],e[N];
int h[N],idx;
void Ins(int a,int b){
e[idx].to=b;e[idx].nxt=h[a];h[a]=idx++;
}
int H[N],len;
void I(int a,int b){
E[len].to=b;E[len].nxt=H[a];H[a]=len++;
}
int rt,stk[N],dfn[N],low[N],Time,dcc_cnt,top,belong[N],vis[N];
bool cut[N];
void tarjan(int u){
dfn[u]=low[u]=++Time;
int s=0;
for(int i=H[u];~i;i=E[i].nxt){
if(vis[i])continue;
vis[i]=vis[i^1]=1;
stk[++top]=i>>1;
int v=E[i].to;
if(!dfn[v]){
tarjan(v);
low[u]=min(low[v],low[u]);
if(dfn[u]<=low[v]){
if(u!=rt||++s>1)cut[u]=1;
dcc_cnt++;
while(1){
int x=stk[top--];
belong[x]=dcc_cnt;
if(x==(i>>1))break;
}
}//tarjan把边映射到点双里
}else low[u]=min(low[u],dfn[v]);
}
}
int p[N][24],dep[N];
void dfs(int u){
vis[u]=1;
for(int i=0;p[u][i];i++)
p[u][i+1]=p[p[u][i]][i];
for(int i=h[u];~i;i=e[i].nxt){
int v=e[i].to;
if(vis[v])continue;//因为有重边所以不能只判断是不是等于父亲节点
dep[v]=dep[u]+1;
p[v][0]=u;
dfs(v);
}
}
int lca(int a,int b){
if(dep[a]<dep[b])swap(a,b);
int d=dep[a]-dep[b];
for(int i=0;d;i++,d>>=1)
if(d&1)a=p[a][i];
if(a==b)return a;
for(int i=20;~i;i--){
if(p[a][i]!=p[b][i]){
a=p[a][i];
b=p[b][i];
}
}
return p[a][0];
}
void init(){
memset(h,-1,sizeof(h));
memset(H,-1,sizeof(H));
memset(p,0,sizeof(p));
memset(dep,0,sizeof(dep));
memset(dfn,0,sizeof(dfn));
memset(belong,0,sizeof(belong));
memset(vis,0,sizeof(vis));
memset(cut,0,sizeof(cut));
top=dcc_cnt=Time=idx=len=0;
}
int main(){
int n,m;
while(~scanf("%d%d",&n,&m)){
if(n==0&&m==0)return 0;
init();
for(int i=1;i<=m;i++){
int a,b;
scanf("%d%d",&a,&b);
I(a,b);I(b,a);
}
for(int i=1;i<=n;i++){
if(!dfn[i]){
rt=i;
tarjan(i);
}
}
int tot=0;
for(int i=1;i<=n;i++){
if(cut[i]){
int u=++tot+dcc_cnt;
for(int j=H[i];~j;j=E[j].nxt){
int v=belong[j>>1];
Ins(u,v);Ins(v,u);//缩点
}
}
}
memset(vis,0,sizeof(vis));
for(int i=1;i<=tot+dcc_cnt;i++)
if(!vis[i])//用vis标记一下,防止重边
dfs(i);
int q;
scanf("%d",&q);
while(q--){
int a,b;
scanf("%d%d",&a,&b);
a=belong[a-1],b=belong[b-1];
printf("%d
",dep[a]+dep[b]-2*dep[lca(a,b)]>>1);
}
}
}