整数规划之割平面法 How and why?
说明
本文并不是一篇教程,只是把学习过程中的不解的地方做记录,解释为什么使用割平面法时添加的约束方程是那个样子的。
割平面法
割平面法的大致思路是通过先求解非整数规划也就是普通线性规划的最优解,对于非整数解通过添加约束条件来使得可行域变小,再重新解加了约束条件的普通线性规划,直到解为整数解。割平面法相对与分支定界法稍微难理解一点,后者非常简单明了,在对非整数解分成大于和小于两个分支搜索结果,而割平面法不容易理解的地方在于添加的约束。
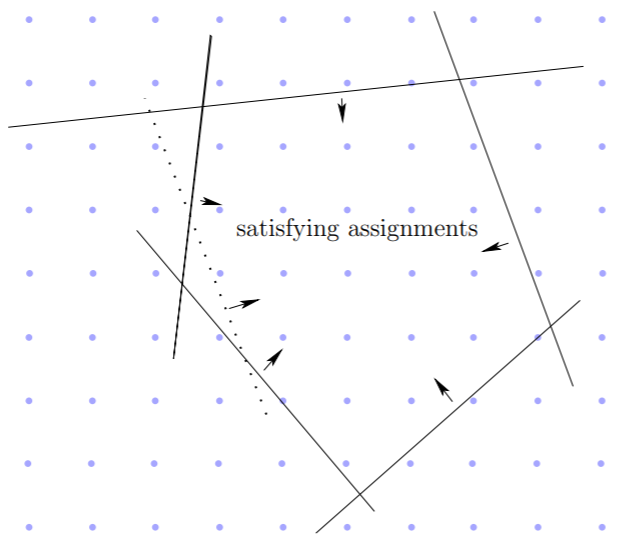
上图中虚线是割平面法添加的约束,将线性规划问题的可行域减小。
下面将以一个例子作为展开,来说明割平面法是如何添加约束的。
假定一个整数规划问题如下:
手动单纯形法解一下非整数的线性规划问题,得到下面的单纯形表:
| 5 | 8 | 0 | 0 | |||
|---|---|---|---|---|---|---|
| Cb | 基 | b | x1 | x2 | s1 | s2 |
| 5 | x1 | 9/4 | 1 | 0 | 9/4 | -1/4 |
| 8 | x2 | 15/4 | 0 | 1 | -5/4 | 1/4 |
| 检验数 | 0 | 0 | -5/4 | -3/4 |
这个时候可以看到解x1和x2都不是整数,于是对x2添加一个约束条件:
How and why
为什么是添加这个约束条件呢?
首先由表中x2那一行我可以得到这个约束等式:
改写一下形式(将整数部分和小数部分分开):
将整数部分移项:
等号左边分为两个部分,可以得到:
那为啥这里可以把等号变成大于等于号呢?可以证明,如果IL和IR是任意两个整数,f为正分数,F为一些正分数的和,使得(IL + F = IR + f),那么一定有:
简单证明:如果F> 1,则F>f;如果0<F<1,则F = f。这样就可以得到小数部分的关系如上了。
在添加约束条件之前的可行域:
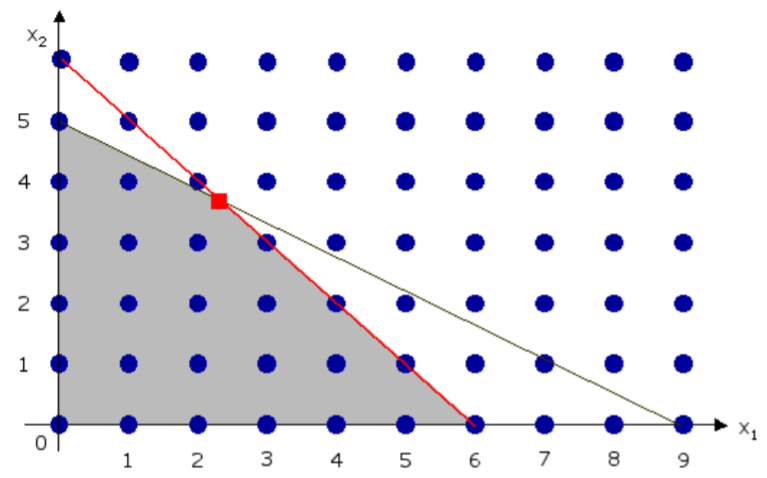
蓝线和红线为两个约束条件,蓝色部分为可行域。
添加约束条件之后的可行域:

蓝色虚线为添加的约束条件。可见约束条件刚好能包含原可行域内所有整数可行解,并且可行域的大小减小了。
实际上,只要能够让可行域的大小减小并且能包含所有整数可行解,无论怎么添加约束条件都是可以的,上述的约束条件添加的方法只是很多方法中的一种,是Gomory第一个发现的,所以很常用。从几何意义上讲,约束条件的添加是对可行域的一次切割,所以称为割平面法。
那为啥要用对偶单纯形法解而不是单纯形法呢?
因为添加了约束,约束肯定是大于等于,再引入新的松弛变量的时候,一定是减去松弛变量等于右边,这个时候松弛变量前面的系数为-1,没办法作为基变量,而如果将不等式两边都取负号,就变成了小于等于,加的松弛变量前面的系数就是1,但是b却成了负值,而对应的对偶问题是有解的,所以用对偶单纯形法解。
还有最后一个问题,为啥每次加的约束都要对b的小数部分最大的那一行加约束,而不是对其他行,或者说所有非整数解都加约束呢?
按照书上的说法是,经验表明,往往加小数部分最大的那一行的约束收敛会更快,那如果把所有非整数解对应的行都加上约束,可行域不是更小了吗,这是不是意味着迭代次数将会减少呢?然而单纯形法的时间复杂度是指数级别的,这样加可能会算的时间更长吧(猜测),需要证明或者验证一下结论。