《机器学习基础》 课程总结(一)
本文不是一篇tutorial,为课程学习记录,仅记录个人认为重要和需要扩展的地方,基础或容易记忆的内容略过。我发现ubuntu系统下的搜狗输入法老有错别字,望谅解。
定义
根据王珏研究员的定义,"令(W)是给定世界的有限或无线所有观测对象的集合,由于我们的观测能力有限,我们只能获得这个世界的一个子集(Q sqsubset W),称为样本集。机器学习的目的在于根据有限的样本集Q,建立可以推算W中对象的预测模型,并使模型对W的预测尽可能为真。"
其认为模型需要注意一致性(W与Q由相同的性质,独立同分布)和泛化性(模型对未知样本的预测能力)。
为什么要独立同分布
首先是要求什么东西独立同分布? 数据之间,也就是样本之间是独立同分布的。抛硬币是一个很好的例子,我们把每次抛硬币的结果当成一个样本,抛十次,就有十个样本了,但是这十次结果都是相互独立的,概率分布相同,所以是独立同分布。
独立的作用是使得可以利用mini batch也就是一小部分样本进行计算,试想如果不独立,每次抽五个样本计算,那么怎么能保证最终的估计是整个真实分布呢?正因为独立了,所以可以用少量样本计算,以小估大。此外,似然估计那里用独立也是为了简化计算。
同分布是为了保证mini batch计算的方向正确,比如一个分布是猫的分布,另一个分布是狗的分布,我们的任务是将猫狗划分为一类,其他动物划分为另一类,如果在mini batch中先拿猫的分布采样的数据训练,下一个mini batch 中再拿狗的分布采样的数据训练(假定猫和狗属于同一类别),就相当于用两个分布的数据在优化,大概率网络很难收敛,特别是这两个分布的差异特别大的时候(显然分布比较接近影响就很小)。就好比走路,一会往左走,一会往右走,可能最终就没走。那如果我们假设他们是同分布的,理论上讲即使是一会拿猫训练一会拿狗训练,对结果也不应该有影响的,所以我们对训练集打乱随机采样,是为了加强这一假设。
当然其实有些任务并不要求独立同分布,我们在很多数据集中看到一些图像是一段视频里每隔一段时间cut下来的一帧数据,这些数据在也不能说是严格iid的,如果是目标检测这样的任务,我们可以假定每帧之间可以iid,因为我的任务不需要考虑帧与帧之间的关系,但如果是跟踪的任务,就需要考虑这些关系了,所以要不要求iid是跟具体任务有关的。异常检测中,有很多异常样本是正常样本的微小变化得到的,与正常样本之间有着很强的关系,但是如果假设样本之间iid,这样异常就很难捕捉,因此,异常检测需要在non-iid数据下捕捉到这种异常。
学习任务
分类问题
对于分类问题,有似然
由于我们假定样本是独立同分布的,所以(p(x) = prod_i p(x_i)),显然是一常数,和数据集有关,那么他们对应的标签也应该满足独立同分布,所以(p(C_i))也是一个常数。
而我们要对似然取极大值,则loss不管那些常数项自然就近似等于
在神经网络中,我们就对(p(C_i|x))进行建模,上式的loss就是交叉熵。
那么问题来了,显然(C_i)是可以有多个取值的,如果不是二分类问题,我们可以取很多值,为什么最终的loss不是把这些loss加起来呢?
事实上,这个问题很显然,因为你的target只有一个取值呀,也就是你的样本只能被分成一类(不考虑类别重叠),所以只需要取target所在类别的结果计算就好了,如果都取然后求和,相当于对一个样本x,他对应的标签出现的概率似然都取最大,这显然不是我们需要的,这里就对应的是pytorch里nn.CrossEntropyLoss的结果。
那又一个问题来了,我们平常看到的交叉熵,形式不是(-sum_i p(C_i|x)log(q(C_i|x)))这样的吗,既然叫nn.CrossEntropyLoss,那为啥不是我们平常看到的交叉熵的形式呢?
事实上呀,(-sum_i p(C_i|x)log(q(C_i|x)))里的(p(C_i|x))的取值只能是0或1,因为对于实际分布p来说,他只能属于一类,所以只保留非0项,结果就和nn.CrossEntropyLoss一样了。而对于二分类问题,pytorch中的nn.BCELoss对应的就是这种结果了,所以本质上都是一样的,基于极大似然导出的结果。
所以呀,一般你用了交叉熵函数作为loss了,你基本就已经假设样本之间独立同分布啦!
回归问题
回归问题一般的loss比较简单,不再赘述。
概率密度估计问题
概率密度估计问题是要根据样本出现的概率去估计整个概率分布。一般的概率密度估计问题的loss可以定义为下式:
似然函数的负对数形式,这让我想起了一个概率密度估计问题,PixelCNN网络,以之前生成的所有像素为条件概率来拟合当前像素概率的概率分布,即(p(x_i|x_1,x_2,...x_{i-1})),因此也是一个概率密度估计问题,最后算loss的时候是用nn.CrossEntropyLoss来计算loss的
显然gt的取值是从0-255的256个离散取值,所以对应的是离散概率分布,(x_i)取值离散,那跟上面分类问题里(p(C_i|x))不是一样了嘛,所以这个式子的loss就是交叉熵。
这也告诉了我们一个结论,当(L(p(x.Theta)))的x取值离散的时候,概率密度的似然就是交叉熵。
学习方法
有监督学习、无监督学习、半监督学习、代价敏感学习、集成学习、增强学习、迁移学习、多任务学习。
其中半监督学习里提到的EM和Co-training两个关键词,记录一下。
EM
EM算法之前也研究过,感觉是类似吉布斯采样那样的步骤,先固定一个再去优化另外一个,这样的策略。但是不知道还可以做半监督学习。其实用起来简单,先依随机概率给未知样本分配soft-label,然后根据所有样本去极大似然估模型参数,然后再固定模型的参数再分配soft-label给随机样本,重复。
Co-training
顾名思义联合训练,即要有两个分类器。
两个分类器C1和C2分别训练两组不同的已标记的数据集D1和D2,两个分类器分别给未标记数据集U打标签,把C1预测的结果挑置信度高的放到D2中继续训练,C2预测的结果挑置信度高的放到D1中训练,重复,直到未标记数据用完。
代价敏感学习
其实就是给常规的分类loss去按照一定的比例去加权,这个我在下面代价敏感错误率和代价曲线那一节有详细写,这里不重复,之前看focal loss的时候就写过类似的。而且focal loss不仅解决了正负样本不平衡问题(加权),而且解决了hard example和easy example的loss分配问题(指数函数)。
假设空间
模型属于由输入空间到输出空间的映射的集合,这个集合就是假设空间(hypothesis space)
归纳偏好
归纳偏好的英文是"Inductive bias",说的是机器学习算法在学习的过程中会倾向于选择某种类型的假设的偏好,比如说,在loss后对参数加了正则项,那么这个偏好产生的结果是算法更倾向于学习一个参数更为稀疏的模型,这种偏好是一种奥卡姆剃刀原则指导下的偏好。显然,还有其他的准则来约束模型。
然后书上推导公式得出 个结论:模型在训练集之外对于所有真实样本的总误差与学习算法是无关的。
上述结论依托于一个假设,所有的“问题”出现的可能性相同,以及我们希望学东西的真实目标函数f是均匀分布的,这在实际当中并不成立。
因而不存在一个机器学习算法对所有问题都能很好解决,因为在所有问题上,任何一个机器学习算法的性能都是一样的,但是具体到某一个问题,算之间的性能就可比了。
机器学习算法的归纳偏好与问题是否匹配,决定了算法本身的性能。
参考:https://www.cnblogs.com/my-python-learning/p/11829548.html
距离测度
距离的定义:
满足下列三个条件的公式成为距离测度(distance metric):
分别为非负性、对称性、三角不等式。
这让我想起了交叉熵函数,他是非对称的,但是却可以用来衡量两个分布之间的距离,为什么呢?
信息论中,熵代表着根据信息的概率分布对信息编码所需要的最短平均编码长度,那么其实交叉熵就是用非真实数据分布来表示真实分布的平均码长,由于熵是自身真实分布对真实分布的表示的最短平均码长,所以使用交叉熵得到的平均码长很定大于真实分布的熵,因此最小化交叉熵来使得真实分布和非真实分布更接近。
然而,交叉熵是非对称的,所以他不是严格意义上的距离,但是可以满足其他两个条件,而且很work、
马氏距离
欧式距离有个问题,就是不同axis之间可能数值差异较大,这样的话,数值大的那个axis在距离中可能导致很大的影响。所以一般我们会对数据不同纬度做归一化,然而"举个一维的栗子,现在有两个类别,统一单位,第一个类别均值为0,方差为0.1,第二个类别均值为5,方差为5。那么一个值为2的点属于第一类的概率大还是第二类的概率大?距离上说应该是第一类,但是直觉上显然是第二类,因为第一类不太可能到达2这个位置。所以,在一个方差较小的维度下很小的差别就有可能成为离群点。"此外,axis之间不独立同分布的时候,一般是不同分布的时候,也可能会导致服从大部分分布的样本和一个利群点对该分布上,某点的距离是一样的,这并不是我们想要的,因为我们想把利群点和符合分布的点分开。
马氏距离的表达式如下:
推导很简单,对于训练集(X_{n imes m}),我们希望找到一个变换矩阵(U),将原坐标系旋转到新的坐标系,令变换后的训练集为(F),则
对(X)而言,其协方差阵为:
对(F)而言,其协方差阵为:
由线性代数的知识我们知道,由于我们希望得到的数据集F的各个维度之间是不相关的,所以F的协方差矩阵应该是diag矩阵,而X的协方差阵是对称矩阵,所以U一定是正交矩阵。(对称阵一定可以找到一个正交阵对角化)
所以变换后的坐标考虑旋转和scale,为
U矩阵是负责旋转的,然后减去在新坐标系下的均值和方差,scale。
所以,马氏距离不仅考虑了维度之间的相关性,通过变换坐标系消除相关性,而且考虑了样本分布的问题,通过scale来解决。
模型评估
交叉验证
概念:交叉验证先将数据集D划分为k个大小相似的互斥子集,每个子集都要尽可能保持数据分布的一致性,然后每次用k-1个子集训练,余下的子集测试,用这k次训练结果的均值来表示一个模型的性能。
在实验的时候,有一些点要注意:
- 由于每个子集要尽可能保持数据分布的一致性,所以最好能够保持类别比例与原数据集一致。因此并不是随机划分。
- 交叉验证并不是要从k个模型中选择一个最佳的模型,如果有m个模型,那么每个模型都要做k次交叉验证,总实验次数是km次,才能说明m个模型性能的好坏。
Bootstrap
方法:每次随机从样本集合D有放回中挑选一个样本,重复n次,用这n个可能有重复的样本作为训练集,那些一次也没有被抽到过的样本均作为测试集。
样本在m次采样中始终不被采样到的概率是((1-frac{1}{m})^m),取极限,则约有(36.8\%)的样本不会被采样到,所以这些样本可以用来作为测试集。
数据集不够的时候,一般可以采用Bootstrap方法。
性能度量
混淆矩阵
针对二分类问题,混淆矩阵为:
| 预测正例 | 预测反例 | |
|---|---|---|
| 实际正例 | TP | FN |
| 实际反例 | FP | TN |
查全率、查准率、PR曲线和F1值
查准率:
顾名思义是准不准(需要注意的是,二分类问题一般只考虑正类这一类别),准不准咋看呢,显然,你预测的东西里面,预测正确的占你所有预测结果的比例应该就是查准率了,所以公式记为(P = frac{TP}{TP + FP})
查全率:
也是顾名思义,全不全,咋看全不全呢,就是你预测的正类数目如果把数据集里所有的正类都包含进去了,那你预测的就很全面,所以很明显,就是你预测的结果里面预测正确的数目与真实数据集里所有正例的数目的比值。(R = frac{TP}{TP + FN})
所以以R为横轴,P为纵轴做的曲线称为PR曲线。
然后有一个问题是,我们训练完一个模型,预测完结果,难道不是只能得到一个P和一个R吗,哪来曲线这一说?
实际上,我们的模型预测的结果是属于正类的概率,而不是直接告诉我们是正类还是父类,这一点是我们人为设置了个阈值比如0.5,大于0.5的为正类,否则为父类。所以呀,通过不管改变这个阈值,就可以得到很多组P和R了,这样就可以画PR曲线了。
具体是咋做的呢,写代码怎么写,才能画一个PR曲线呢?
将预测的概率从小到达排序,每次向右移动一个样本距离,相当于每次改变一次阈值,将阈值左边的认为是父类,右边认为是正类,每次得到一个P和R,绘制。
Coding:
from matplotlib import pyplot as plt
import numpy as np
def PR(pred,gt):
tp = ((pred == 1) & (gt == 1)).sum()
fp = ((pred == 1) & (gt == 0)).sum()
fn = ((pred == 0) & (gt == 1)).sum()
tp = np.float(tp)
fp = np.float(fp)
fn = np.float(fn)
p = tp / (tp + fp)
r = tp / (tp + fn)
return p,r
def ROC(pred,gt):
tp = ((pred == 1) & (gt == 1)).sum()
fp = ((pred == 1) & (gt == 0)).sum()
up = np.sum(gt)
un = np.sum(1-gt)
tpr = tp / up
fpr = fp / un
return tpr,fpr
if __name__ == "__main__":
x = np.array([0.3,0.6,0.9,0.1])
y = np.array([1,0,1,1])
idx = np.argsort(x)[::-1]
x = x[idx]
y = y[idx]
pp = sorted(list(set(x)))[::-1]
ps = []
rs = []
for p in pp :
pred_label = np.where(x>=p,1,0)
gt = y
p,r = PR(pred_label,gt)
print(p,r)
ps.append(p)
rs.append(r)
plt.plot(rs,ps)
plt.show()

??? 啥情况?咋跟书上那个看起来很漂亮的曲线不一样啊??
实际上我并没有画错,书上也在小字部分说了“PR曲线通常非单调、不平滑”,所给的例子是特别好看的例子。。。
F1值:
对P和R取调和平均:(F1 = frac{2PR}{P+R})
ROC曲线和AUC
我们说PR曲线的性质太差了,不画不知道,一画吓一跳,有没得性质好点的,单调的曲线呢?
ROC曲线就是呀!
ROC曲线横纵坐标分别是FPR和TPR,定义为:
称为真正例率(所有正例里面你预测正确的比例)和假正例率(所有负例里面你给错误预测成正例的比例)。好像根据名字没办法呢直接联想到公式吼。所以名字起得太烂了。
他的性质就好很多了,一来是单调增,而来也好理解。首先,也是一样的排序,一样的去阈值移动,分母我们看一下,都是针对整个训练集,是所有正例,或者是所有负例,所以分母其实是不随着阈值移动变化的,所以变的就只有分子部分,而每移动一次阈值,就会走过一个样本,我们会给他一个pred标签为正类,那么这个时候,他要么是分对了,要么是分错了,分对了,TPR的分子就会+1,分错了,FPR的分子就会+1,这样在图上,就相当每次阈值移动一下,我们在图上要么画一条水平线,要么画一条竖直线。然而,还有种情况没考虑到,就是有多个样本他的预测概率是一样的,然是呢,他们的gt可能不同,比如两个样本都预测为0.9,但是一个gt是0,一个gt是1,那么阈值移动的时候就会走过两个样本,这时候画的既不是水平线也不是竖直线,而是倾斜线。这样就完全理解ROC曲线这个东西的画法了。
import numpy as np
def ROC(pred,gt):
tp = ((pred == 1) & (gt == 1)).sum()
fp = ((pred == 1) & (gt == 0)).sum()
up = np.sum(gt)
un = np.sum(1-gt)
tpr = tp / up
fpr = fp / un
return tpr,fpr
if __name__ == "__main__":
x = np.array([0.3,0.6,0.4,0.4,0.1])
y = np.array([1,0,1,0,1])
idx = np.argsort(x)[::-1]
x = x[idx]
y = y[idx]
pp = sorted(list(set(x)))[::-1]
tprs = []
fprs = []
for p in pp:
pred_label = np.where(x>=p,1,0)
gt = y
tpr,fpr = ROC(pred_label,gt)
tprs.append(tpr)
fprs.append(fpr)
print(fprs,tprs)
plt.plot(fprs,tprs)
plt.show()

AUC指的就是ROC曲线下面积哈。
目标检测中的评估方式
AP和MAP
AP就是PR曲线下的面积。
那MAP是啥呢?
我们说,对于二分类问题,我们才有正类负类这样的说法,所以我们能简单求一个AP,MAP顾名思义应该是平均的AP,目标检测任务中往往目标类别是大于1的,有多个类别,那么背景其实也属于一类,我们把背景称为负类,其他的都是正类。这样,每类与背景做一次AP,就能得到多个AP了,将这些AP平均,就是MAP。
代价敏感错误率与代价曲线
上面的问题我们考虑二分类问题只去关心正类的错误率或者其他指标,但实际上一些问题中,我们也许要关心多个类别的错误率,而不是简单只考虑一个类别的。
比如说,对于一个三分类问题,gt为0的样本可能被分到1或者2,被分到1的有一些错误率,被分到2的也有一些错误率,而这些错误率我们不能去平等看待,为什么呢,因为类别不平衡呀!如果我们训练集大部分都是类别0的样本,那么类别0的样本被错分为其他类别的比例为降低,也就是说,类别为0的样本在其他类别上的错误率很低,其他类别错分为0类的错误率可能很高,这就是类别不平衡带来的问题。
一个好的办法就是加权,我们上面其实也简单说了一下,怎么加权,按照类别比例加权。
以二分类为例,假设第0类第1类的样本比例为(p:(1-p)),用(cost_{01})表示正类被误分为反类的代价,同样的(cost_{10})表示反类被误分为正类的代价。则如果考虑所有的类别比例,那么平均代价可以表示为:
第一行到第二行是根据TPR和FPR的定义,两项分别除以(m^+)和(m^-)分然后再乘上。I是指示函数,m是样本总数,很好推。
同样地,由于类别不平衡,所以ROC曲线也不适用了,因为FPR和TPR没考虑类别不平衡。搞了个代价曲线,对于二分类问题,定义曲线横轴为正例概率代价(P(+)_{cost}),纵轴为(cost_{norm})
公式也不难理解,分母部分是根据类别比例的加权代价,分子部分分别为正例的加权代价和平均代价。
好,那么代价曲线要如何理解呢?
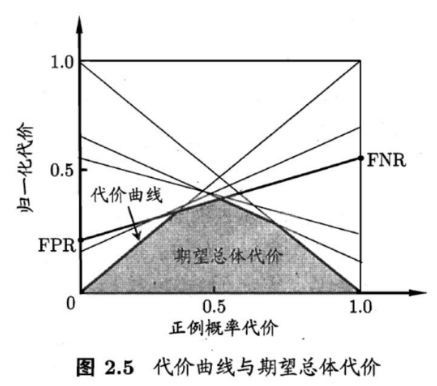
首先我们知道有一些变化量,
- 分类阈值,阈值滑动会导致FPR和FNR变化。
- 正负类别比例。
老师PPT上写到“ROC曲线上一点,对应的是代价曲线上的一条线段”,可以这么理解,ROC曲线上的一点,表明分类阈值是定的,所以FPR和FNR是定的,同时,也要求分类器是定的,在这样的情况下(只有正负类别比例在变),对应的代价曲线应该是一条直线(线段),为什么呢?
同理
所以可得
即斜率为一定值,所以是一条直线。
所以图上的两个截点就很好理解了。
那么如果考虑所有情况,也就是不同分类器和不同阈值的变化,那么直线就会不断改变,我们取所有直线的下界,所围成的面积也就是对所有情况的积分,表示的就是期望总体代价了。
下面就是写代码,找了一圈没找到开源,反正自己理解了,自己写呗。
from matplotlib import pyplot as plt
import numpy as np
def PR(pred,gt):
tp = ((pred == 1) & (gt == 1)).sum()
fp = ((pred == 1) & (gt == 0)).sum()
fn = ((pred == 0) & (gt == 1)).sum()
tp = np.float(tp)
fp = np.float(fp)
fn = np.float(fn)
p = tp / (tp + fp)
r = tp / (tp + fn)
return p,r
def ROC(pred,gt):
tp = ((pred == 1) & (gt == 1)).sum()
fp = ((pred == 1) & (gt == 0)).sum()
up = np.sum(gt)
un = np.sum(1-gt)
tpr = tp / up
fpr = fp / un
return tpr,fpr
def Cost(pred,gt):
tpr,fpr = ROC(pred,gt)
fnr = 1 - tpr
slope = (fnr - fpr)
b = fpr
return slope, b
if __name__ == "__main__":
x = np.array([0.3,0.6,0.4,0.4,0.1])
y = np.array([1,0,1,0,1])
idx = np.argsort(x)[::-1]
x = x[idx]
y = y[idx]
pp = sorted(list(set(x)))[::-1]
slopes = []
bs = []
#tprs = []
#fprs = []
for p in pp:
pred_label = np.where(x>=p,1,0)
gt = y
slope,b = Cost(pred_label,gt)
slopes.append(slope)
bs.append(b)
xs = np.arange(1,step = 0.1)
ys = np.ones_like(xs) * 1000
for slope,b in zip(slopes,bs):
y_temp = xs * slope + b
ys = np.minimum(ys,y_temp)
plt.plot(xs,ys)
plt.show()
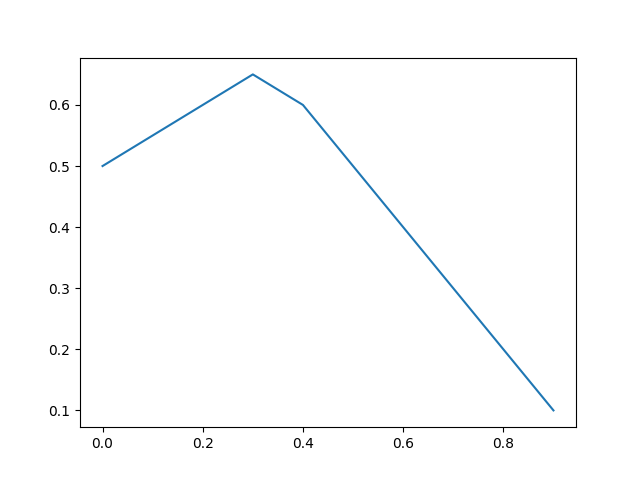
其实还有个问题,为啥我的曲线没有经过(0,0)和(1,0)很简单,因为我给的FPR和FNR里没有0呀!
线性回归
loss function:
原始的线性回归有闭式解:
很显然,((X^TX))满秩才能得到上式解,X为(m imes n)的矩阵,因此X的秩肯定小于等于(min{m,n}),(X^TX)为(n imes n)矩阵,因此如果n很大,m很小,((X^TX))的秩肯定小于等于m,那么就一定小于等于n,此时一定不满秩。也就是数据维度比样本数多的情况下不满秩。
所以我们一般用梯度下降法来解线性规划问题,梯度下降下面会详细说,这里先继续讲线性回归。
对于原始的线性回归问题虽然能求解,但是模型呀太容易过拟合了,如果特征非常多,模型会尽量把每个特征都用上,然而事实上某些任务只用一些特征就能拟合这一任务了。
我们有一种观点是,模型复杂度越大,参数量越多,越容易过拟合。所以防止过拟合的方式就是减少模型参数,也就是让参数更稀疏。过多的参数量会使得bias很小,因而导致过拟合。
很容易想到的办法就是用L0范数,完完全全可以降低稀疏性,也就是利用奥卡姆剃刀原理,在loss函数后面加个对参数w的L0范数,来约束模型复杂度,这样能够适当增加bias,减少过拟合。
事实情况是L0范数一来不可导,但是对不可导的问题我们也有办法求解,二来尽管能求解,但是很难解。
用L1范数求解难度会小一点,有那个坐标下降法可以求,下次更新这篇博客补上。
L2范数能直接得到闭式解:
由于加了个(lambda I),所以一定有逆,所以给数据集就可以直接算出参数了,不需要啥梯度下降。
梯度下降
Gradient Descent
最速下降法
由于步长(eta)人工确定是超参,可以通过搜索的方式来搜索到一个使得目标函数值下降最快的步长,比如可以采用0.618法,假定步长取值为0-1之间的值,不断舍去区间直到区间长度足够小,让此时的步长为最终步长。
当w(t)已知的时候,极小微分即梯度也已知时,(L(w(t) - eta g))为关于(eta)的函数,求该函数极值即可确定(eta)
此方法为最速下降法。
牛顿法
泰勒展开
上式对x求导 = 0,有
上式有一个条件,(Delta x = |x - x_k|)很小的时候才成立,即(|Delta x| <d),而d正比于学习率,因此写成
这就是牛顿法的公式,实际上,如果只利用一阶微分,而不做二阶近似,就是一般的梯度下降算法
此时有
我们要让f(x)尽可能小,所以(f'(x_k)(x-x_k))必须小于0,那么(Delta x = x - x_k)肯定得与(f'(x_k))也就是梯度的方向反向,也就是符号与之相反,而这个式子有一个约束,就是在极小范围内去搜索一个方向使得函数值下降才能保证泰勒近似可以这么表示,因此(|Delta x| <d),而d正比于学习率,所以我们可以用较小的学习率来去做梯度下降,因此在学习率较大的时候会破坏泰勒近似,所以这个时候梯度下降不起作用。多维的情况在下面。
此外,牛顿法的分母项可以用(sqrt{sum f'(x_t)^2})来近似,为adagrad.
Learning Rate的调整
- Simple idea: lr随着step调整越来越小,(eta(t) = frac{eta}{sqrt{t+1}})
- Adagrad
分子的g(t)是一阶微分,分母部分是想要对二次微分的近似,而一次微分除以二次微分是best step。
- SGD
随机梯度下降算法,每次只拿一个sample出来算loss更新参数。
4. RMSProp
对比AdaGrad,分母部分的求和换成了加权求和,权重是超参。
- Adam
Adam = RMSProp + Momentum
Feature Scaling
把输入的各个量纲统一,这样可以保证参数对loss的贡献都是相差不大的,这样在同一的lr下容易调整。
常用的办法是减去均值除以方差.