大整数乘法——分治算法的时间复杂度

　　1.1原始的低效算法

　　

　　我们将n位（为方便讨论简化问题，我们假设n是2的幂）十进制整数（二进制也可以）X、Y都分为2段，每段的长度是n/2位。

 

　　如果现在直接用递归或分治进行编程，其算法复杂度为： 

　　其中：T(n)代表规模为n的问题，系数4表示问题缩小到T(n/2)时，包含四次乘法（上式中AC/AD/BC/BD四次）

这是在没有进行优化情况下的算法复杂度（注意，此处虽然用了分治思想，但分治并不会降低算法复杂度，反而因其需要使用栈，增加了算法的空间复杂度）。

　　1.2高效的算法（运用了数学的小技巧）

　　

　　我们知道，大整数乘法的基本运算是“乘法”运算，我们可以通过减少乘法的次数来降低算法复杂度！

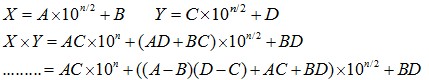
　　从公式中可以发现，原来有四个基本乘积项：AC、AD、BC、BD，现在只有三个基本乘积项：（A-B)(C-D)、AC、BD。乘法运算的数量降低了，下面看看其复杂度变化：

复杂度从n²降到n^1.59

　　1.3补充

　　有的小伙伴可能会问了，如果不分成两段，分成三段，四段甚至n段的时候时间复杂度会降低，结论是：

　　

　　在大整数乘法中，当把大整数分为2段时，算法时间复杂度最低n^1.59

　　随着段数逐渐增加，算法的时间复杂度也随之增加，当分段增加到n段时，算法时间复杂度退化到n²