题目描述
不妨认为舞厅是一个N行M列的矩阵,矩阵中的某些方格上堆放了一些家具,其他的则是空地。钢琴可以在空地上滑动,但不能撞上家具或滑出舞厅,否则会损坏钢琴和家具,引来难缠的船长。每个时刻,钢琴都会随着船体倾斜的方向向相邻的方格滑动一格,相邻的方格可以是向东、向西、向南或向北的。而艾米丽可以选择施魔法或不施魔法:如果不施魔法,则钢琴会滑动;如果施魔法,则钢琴会原地不动。
艾米丽是个天使,她知道每段时间的船体的倾斜情况。她想使钢琴在舞厅里滑行的路程尽量长,这样1900 会非常高兴,同时也有利于治疗托尼的晕船。但艾米丽还太小,不会算,所以希望你能帮助她。
输入格式
输入文件的第一行包含5个数N, M, x, y和K。N和M描述舞厅的大小,x和y为钢琴的初始位置;我们对船体倾斜情况是按时间的区间来描述的,且从1开始计算时间,比如“在[1, 3]时间里向东倾斜,[4, 5]时间里向北倾斜”,因此这里的K表示区间的数目。
以下N行,每行M个字符,描述舞厅里的家具。第i 行第j 列的字符若为‘ . ’,则表示该位置是空地;若为‘ x ’,则表示有家具。
以下K行,顺序描述K个时间区间,格式为:si ti di(1 ≤ i ≤ K)。表示在时间区间[si, ti]内,船体都是向di方向倾斜的。di为1, 2, 3, 4中的一个,依次表示北、南、西、东(分别对应矩阵中的上、下、左、右)。输入保证区间是连续的,即
s1 = 1 ti = si-1 + 1 (1 < i ≤ K)
tK = T
输出格式
输出文件仅有1行,包含一个整数,表示钢琴滑行的最长距离(即格子数)。
样例1输入
4 5 4 1 3
..xx.
.....
...x.
.....
1 3 4
4 5 1
6 7 3
样例1输出
6
说明/提示
钢琴的滑行路线:
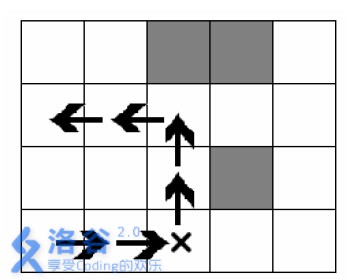
钢琴在“×”位置上时天使使用一次魔法,因此滑动总长度为6。
【数据范围】
50%的数据中,1≤N, M≤200,T≤200;
100%的数据中,1≤N, M≤200,K≤200,T≤40000。
首先考虑对于时间t来dp: f[t][i][j]表示在第t时刻在第i行第j列所能获得的最长距离。
转移方程:f[t][i][j]=max(f[t-1][i][j],f[t][i*][j*]+1)(i*,j*为上一个合理的位置)
这样时间复杂度为O(TNM),可以过50%,但对于100%TLE且MLE。 所以必须优化,首先把时间t换成区间k,
令f[k][i][j]表示在第k段滑行区间中在位置i,j所能获得最长距离 注意到在第k段时间内只能向某个方向最多走x步(x为区间长度),
得到转移方程 f[k][i][j]=max(f[k-1][i][j],f[k][i*][j*]+dis(i,j,i*,j*))(i*,j*为上一个合理的位置)
这个做法的时间复杂度是O(kn^3),会超时,需要进一步优化 用单调队列优化掉内层的一个n,就可以做到O(kn^2),
可以AC,本代码中还使用了滚动数组优化 用单调递减队列求最大值时,遇到障碍清空整个队列即可,另外队列比较时需要加上偏移量dis
#include<bits/stdc++.h>
#define MAXN 205
using namespace std;
int n, m, sx, sy, K, ans, dp[MAXN][MAXN];
int dx[5]={0, -1, 1, 0, 0},
dy[5]={0, 0, 0, -1, 1};
struct node{
int dp, pos;
}q[MAXN]; //q为单调递减队列,要存位置信息用来计算共走了几步
char map1[MAXN][MAXN];
void work(int x,int y,int len,int d){ //第k个区间的时长为len,方向为d,起点坐标x,y
int head=1,tail=0;
for(int i=1;x>=1&&x<=n&&y>=1&&y<=m;i++,x+=dx[d],y+=dy[d])
if(map1[x][y]=='x')
head=1,tail=0; //遇到障碍,清空队列
else{
while(head<=tail&&q[tail].dp+i-q[tail].pos<dp[x][y])
tail--;
q[++tail] = node{dp[x][y], i}; //当前值入队列
if(q[tail].pos-q[head].pos>len)
head++; //队列长度超过len时队首弹出
dp[x][y]=q[head].dp+i-q[head].pos; //最优解是队首元素+移动距离
ans = max(ans, dp[x][y]); //记录结果
}
}
int main(){
scanf("%d%d%d%d%d",&n,&m,&sx,&sy,&K);
for(int i = 1; i <= n; i++)
scanf("%s", map1[i] + 1);
memset(dp, 0xf3, sizeof(dp));
dp[sx][sy] = 0; //初始化,只有初始位置是0,其他都是负无穷
for(int k=1,s,t,d,len;k<=K;k++){
scanf("%d%d%d",&s,&t,&d);
len=t-s+1;
if(d==1)
for(int i=1;i<=m;i++)
work(n, i, len, d);
if(d==2)
for(int i=1;i<=m;i++)
work(1, i, len, d);
if(d==3)
for(int i=1;i<=n;i++)
work(i, m, len, d);
if(d==4)
for(int i=1;i<=n;i++)
work(i, 1, len, d);
}
printf("%d", ans);
}