摘要:
1.数据增强是什么?
2.为什么要数据增强?
3.常见的数据增强举例
内容:
1.数据增强是什么?
数据增强,是指对(有限)训练数据通过某种变换操作,从而生成新数据的过程。
2.为什么要数据增强?
首先要说明一些机器学习中的过拟合和经验误差与泛化误差的概念。
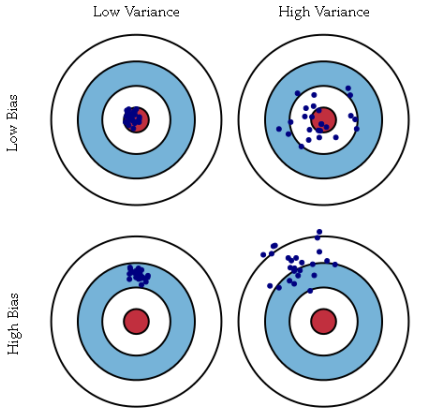
举一个打靶子的例子:
右上角的图,每一镖都比较接近靶心,但是却很分散,我们把机器学习中的这种预测结果和实际结果很接近,但预测的结果很分散的情况叫做高方差,也就是我们经常说的过拟合;
左下角的图,每一镖都偏离靶心,但是却很聚集,我们把机器学习中的这种预测结果和实际结果差别很大,但预测的结果很集中的情况叫做高偏差,也就是我们经常说的欠拟合;
左上角的几乎我们每一镖都命中了靶心,这种情况是最理想的,我们把这种情况称之为低偏差,低方差;
右下角的图我们几乎每一镖都没有命中靶心,这种情况是我们最不想遇到的,也就是说是高偏差,高方差;
再深入一些,很能有人会问看图我们看懂了,可是实践中我们怎么判断哪些情况是过拟合,哪些情况是欠拟合呢?这里就要聊聊训练误差和测试误差了。
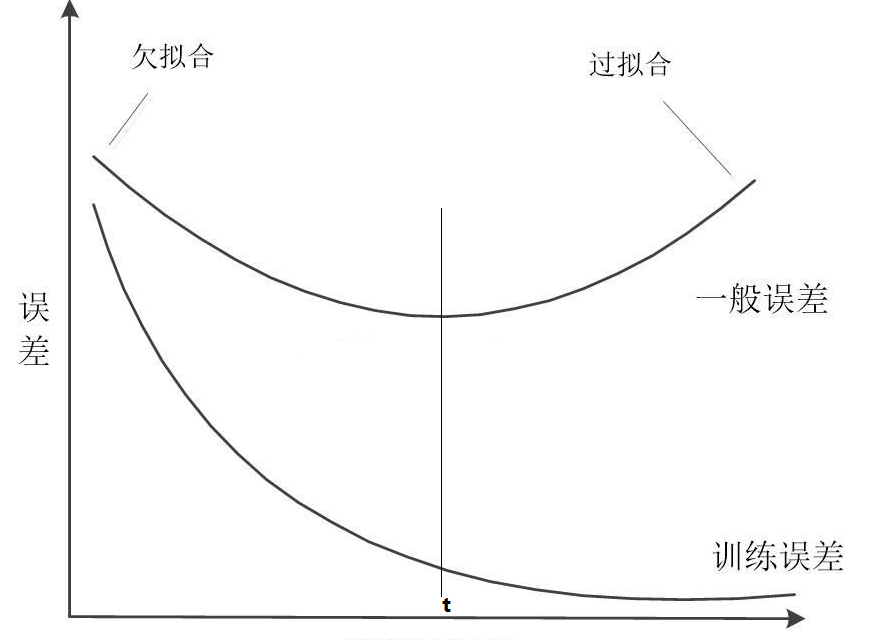
在模型训练的过程中,训练误差是不断下降的,但是测试(一般)误差在下降到一定程度之后就会停止或者上升。这里我标t的垂线的地方就是一个拐点(分界点),
这种在拐点之前模型一直没有达到最优的情况就很明显可以断定为欠拟合,而在这个拐点之后模型在训练集上表现很好,但是在测试集上却在下降的情况也可以断定为过拟合。
最后,有小伙伴会问,我现在会识别什么是欠拟合什么是过拟合了,但是识别之后我应该怎么做呢?
这个问题问得很好啊!我们这里简单分析也为什么会出现过拟合和欠拟合,以及给出简单的解决方案。
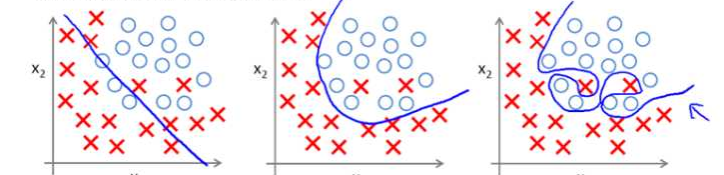
我们有一个二分类(需要预测是不是)的问题,这里红×代表”不是“(负类),圆圈代表”是“(正类)。为了可视化方便,我们这里的模型就是一条蓝色的线。
学过初等数学的小伙伴肯定知道,图一的模型就是一条直线,解析式可以写成y = ax + b,但不幸的是有两个正类被错分成了负类,五个负类被错分成了正类;
图二的模型是一个二次曲线,或者叫抛物线,解析式可以写成y= a*x^2+bx+c,虽然模型复杂了,分类能力强了,但是还有两个被分错了;
最后一张图的模型是n项式,解析式可以写成y= a(1)*x^(n1)+bx^(n1-1)+...+a(n),总算把所有数据都分错了,这时候你很高兴,拿这这个模型去预测新数据,结果却发现预测出来的结果很不像你想象中的那么好,这是为什么呢?
那么头脑风暴的时候到了,你集合了多个小伙伴一起来讨论这个问题。
A说:图1肯定是欠拟合了,但是你增加了模型的复杂程度,所以图2解决了欠拟合。
B说:图二可能也是欠拟合,所以你增加了模型复杂程度,但是也增加了过拟合的风险。
C说:可以增加模型复杂度的同时观测测试误差,直到测试误差下降就停止增加模型复杂度。
D说:可是现在已经发现过拟合了,我觉得可以再增加数据,把模型强行纠正过来。或者增大模型误分的惩罚。
很好,现在我们实现第一种思路,增加数据,但是有问题,大多数情况下我们能收集到的数据就这么多(比如参加数据竞赛,主办方就指定有4w样本),这个时候怎么办?
这时候我们就可以用上数据增强这个利器了,下面围绕图像领域主要介绍一下这部分的内容:
3.常见的数据增强举例

哇,小伙伴们惊呆了,这一张图片变成了76张图片,那么这些是怎么做的呢?
A说:我知道,我知道!第一排做了旋转;
B说:我看到有的图片颜色不一样,是不是做了滤镜啊
C说:有的图片还加了马赛克,挡住了头部和背景
D说:有的看着很清楚,有的就很模糊,像素也不一样。
那么现在我们总结下:
第一,对颜色的数据增强,包括色彩的饱和度、亮度和对比度(contrast)等方面;
第二,对图像进行裁剪(flip),平移(shift),缩放(zoom)和旋转(Rotation/reflection)。
有小伙伴弱弱的问:不对啊,我们不是在处理图像啊,搞得那么复杂。我们的数据是1234这些数字,有没有办法?
我们可以对数据做归一化(取值0-1),标准化(均值为0,方差为1),这个就类比图像中的缩放;
或者随机采样每次都随机采样一些样本(一行数据)和特征(一列数据)。