1、删除链表中重复节点
在一个排序的链表中,存在重复的结点,请删除该链表中重复的结点,重复的结点不保留,返回链表头指针。 例如,链表1->2->3->3->4->4->5 处理后为 1->2->5。
class Solution: def deleteDuplication(self, pHead): # write code here # 判断链表是否为空 if not pHead: return None pPreNode = None #存储要删除节点的前一个节点 pNode = pHead #定义起始节点 #开始循环 while pNode: pNext = pNode.next needDelete = False #判断相邻的两个节点值是否相等 if pNext and pNext.val == pNode.val: needDelete = True #如果不相等就后移一个, pPreNode指向最前面的节点 if not needDelete: pPreNode = pNode pNode = pNode.next #如果相等就开始删除 else: val = pNode.val #初始化要删除节点的值 pDeleteNode = pNode #定义要删除的节点 #判断当前要删除的节点是否和val相等以及是否为空 while pDeleteNode and pDeleteNode.val == val: pNext = pDeleteNode.next del pDeleteNode #删除节点 pDeleteNode = pNext #节点后移 #如果要删除的节点包含初始的头结点,那就需要将头结点移到当前节点的位置 if not pPreNode: pHead = pNext #如果要删除的节点不包含头结点,则将节点进行连接 else: pPreNode.next = pNext #开始从最新的节点开始遍历 pNode = pNext #返回头结点 return pHead
class Solution: def deleteDuplicates(self, head: ListNode) -> ListNode: ans = head while head != None: if head.next != None and head.next.val == head.val: head.next = head.next.next else: head = head.next return ans
class Solution: def deleteDuplication(self, pHead): # write code here if not pHead or not pHead.next:#如果链表为空或只有一个元素,直接返回 return pHead if pHead.val==pHead.next.val:#如果当前结点与下一结点重复,继续查找是否还有重复的 p=pHead.next.next while p and p.val==pHead.val:#如果p结点不为空且其值与当前重复的结点(pHead)相等 p=p.next#p继续往后移位查找,直到没有重复的 return self.deleteDuplication(p)#递归调用函数对头结点为p的链表进行处理 #如果当前结点与下一结点不重复,递归调用函数对头结点为pHead.next的链表进行处理 pHead.next=self.deleteDuplication(pHead.next) return pHead
2、链表中环的入口节点
给一个链表,若其中包含环,请找出该链表的环的入口结点,否则,输出null。
思路1:使用辅助存储空间。遍历链表,环的存在,遍历遇见的第一个重复的即为入口节点。
class Solution: def EntryNodeOfLoop(self, pHead): # write code here List=[] p=pHead while p: if p in List: return p else: List.append(p) p=p.next
思路2:
用快慢指针判断有没有环;
若有,返回快慢指针相遇时的指针,此时指针必定相遇在环中;
遍历环,得到环的数目n;
一个指针先走n步,另一个指针再开始走(它们速度相同),它们相遇的地方就是入口(解释:假设链表起始位置到环的入口节点距离为k,当后走的指针移动k步到达入口结点时,先走的指针移动距离为n+k,刚好多走了一个环的距离,所以又移动到了入口结点,此时两指针相遇)。
class Solution: def EntryNodeOfLoop(self, pHead): # write code here #判断是否有环,以及得到相遇节点 meetingNode = self.MeetingNode(pHead) if not meetingNode: return None #得到环节点的数目 nodenum = 1 pNode = meetingNode while pNode.next != meetingNode: pNode = pNode.next nodenum += 1 #寻找入口结点 pNode1 = pHead for i in range(nodenum): pNode1 = pNode1.next pNode2 = pHead while pNode1 != pNode2: pNode1 = pNode1.next pNode2 = pNode2.next return pNode1 def MeetingNode(self, pHead): if not pHead: return False fast = pHead slow = pHead while fast and fast.next and fast.next.next: fast = fast.next.next #之前写错成fast= phead.next.next slow = slow.next if fast == slow: return fast return False
关于快慢指针,通俗解释:
首先创建两个指针1和2(在java里就是两个对象引用),同时指向这个链表的头节点。然后开始一个大循环,在循环体中,让指针1每次向下移动一个节点,让指针2每次向下移动两个节点,然后比较两个指针指向的节点是否相同。如果相同,则判断出链表有环,如果不同,则继续下一次循环。
例如链表A->B->C->D->B->C->D,两个指针最初都指向节点A,进入第一轮循环,指针1移动到了节点B,指针2移动到了C。第二轮循环,指针1移动到了节点C,指针2移动到了节点B。第三轮循环,指针1移动到了节点D,指针2移动到了节点D,此时两指针指向同一节点,判断出链表有环。
此方法也可以用一个更生动的例子来形容:在一个环形跑道上,两个运动员在同一地点起跑,一个运动员速度快,一个运动员速度慢。当两人跑了一段时间,速度快的运动员必然会从速度慢的运动员身后再次追上并超过,原因很简单,因为跑道是环形的。
3、用两个栈实现队列
用两个栈来实现一个队列,完成队列的Push和Pop操作。 队列中的元素为int类型。
分析:
队列的特性是:“先入先出”,栈的特性是:“先入后出”
当我们向模拟的队列插入数 a,b,c 时,假设插入的是 stack1,此时的栈情况为:
- 栈 stack1:{a,b,c}
- 栈 stack2:{}
当需要弹出一个数,根据队列的"先进先出"原则,a 先进入,则 a 应该先弹出。但是此时 a 在 stack1 的最下面,将 stack1 中全部元素逐个弹出压入 stack2,现在可以正确的从 stack2 中弹出 a,此时的栈情况为:
- 栈 stack1:{}
- 栈 stack2:{c,b}
继续弹出一个数,b 比 c 先进入"队列",b 弹出,注意此时 b 在 stack2 的栈顶,可直接弹出,此时的栈情况为:
- 栈 stack1:{}
- 栈 stack2:{c}
此时向模拟队列插入一个数 d,还是插入 stack1,此时的栈情况为:
- 栈 stack1:{d}
- 栈 stack2:{c}
弹出一个数,c 比 d 先进入,c 弹出,注意此时 c 在 stack2 的栈顶,可直接弹出,此时的栈情况为:
- 栈 stack1:{d}
- 栈 stack2:{}
根据上述栗子可得出结论:
1.当插入时,直接插入 stack1.
2.当弹出时,当 stack2 不为空,弹出 stack2 栈顶元素,如果 stack2 为空,将 stack1 中的全部数逐个出栈,然后入栈 stack2,再弹出 stack2 栈顶元素。即stack1用作入队列,stack2用作出队列。
代码很简单
# -*- coding:utf-8 -*- class Solution: def __init__(self): self.stack1 = [] self.stack2 = [] def push(self, node): # write code here self.stack1.append(node) def pop(self): # return xx if self.stack2 == []: while self.stack1: self.stack2.append(self.stack1.pop()) return self.stack2.pop()
4、滑动窗口的最大值
给定一个数组和滑动窗口的大小,找出所有滑动窗口里数值的最大值。例如,如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3,那么一共存在6个滑动窗口,他们的最大值分别为{4,4,6,6,6,5}; 针对数组{2,3,4,2,6,2,5,1}的滑动窗口有以下6个: {[2,3,4],2,6,2,5,1}, {2,[3,4,2],6,2,5,1}, {2,3,[4,2,6],2,5,1}, {2,3,4,[2,6,2],5,1}, {2,3,4,2,[6,2,5],1}, {2,3,4,2,6,[2,5,1]}。
先上代码:
class Solution: def maxInWindows(self, num, size): # write code here i = 0 #i表示当前窗口中的最后一个数字下标 queue = [] #存放可能是最大值的元素的下标,注意存放的是下标。 res = [] #存放最大值元素 while size > 0 and i < len(num): #判断queue[0]是否还在当前窗口中 if len(queue)>0 and i-size+1 > queue[0]:#仔细琢磨if中的第二个限制条件 queue.pop(0) #如果queue非空,且queue中第一个下标即queue[0]小于当前窗口的最左端元素的下标索引,则删除queue[0].否则不执行出队操作。 #如果有num[i]更大,那么目前队列中的队尾数字不可能成为最大值的下标,删除它 while len(queue)>0 and num[queue[-1]] < num[i]: queue.pop() queue.append(i) #i=size-1时,第一个窗口建立完成,开始记录最大下标 if i >= size - 1: res.append(num[queue[0]]) i += 1 return res
这道题目leetcode难度:困难。所以逻辑想清楚。这个解法用的双端队列思想。
关于这一句:
if len(queue)>0 and i-size+1 > queue[0]:
解释一下,顺便勾勒整个代码实现逻辑:
比如, {[2,3,4],2,6,2,5,1} ,第一个窗口尚未构建完成的时候,len(queue)>0好理解,下面分析:
i-size+1 > queue[0]
第一次滑动刚开始,第一个元素值是2,下标i=0,显然不满足上述if条件,同理也不满足接下来的两个条件,所以不执行对应语句,第一次只能执行的语句是:
queue.append(i)
i += 1
此时i更新为1,对应的元素值为3.继续新一轮条件判断,此时len(queue)=1,queue[0] =0,所以i-size+1 = 1-3+1 = -1,-1不满足>queue[0]的条件,故仍然不执行第一个条件下的语句,
以此类推,继续判断即可。
5、从尾到头打印链表
输入一个链表,按链表从尾到头的顺序返回一个ArrayList。
直接法:从头到尾遍历,然后逆序输出
class Solution: # 返回从尾部到头部的列表值序列,例如[1,2,3] def printListFromTailToHead(self, listNode): # write code here res = [] while listNode: res.append(listNode.val) listNode = listNode.next return res[::-1]
跟上述方法逻辑一致,但是用栈再规范实现一遍:
class Solution: # 返回从尾部到头部的列表值序列,例如[1,2,3] def printListFromTailToHead(self, listNode): # write code here if not listNode: return [] temp = [] res = [] while listNode: temp.append(listNode.val) listNode = listNode.next while temp: res.append(temp.pop()) return res
来一个据说大部分人一看就会,一写就废的递归:
class Solution: def printListFromTailToHead(self, listNode): res=[] def printListnode(listNode): # write code here if listNode: printListnode(listNode.next)#先递归到最后一层 res.append(listNode.val)#添加值,退出函数,返回到上一层函数中的这行,继续添加值 printListnode(listNode) return res
6.相交链表
编写一个程序,找到两个单链表相交的起始节点。
如下面的两个链表:

在节点 c1 开始相交。
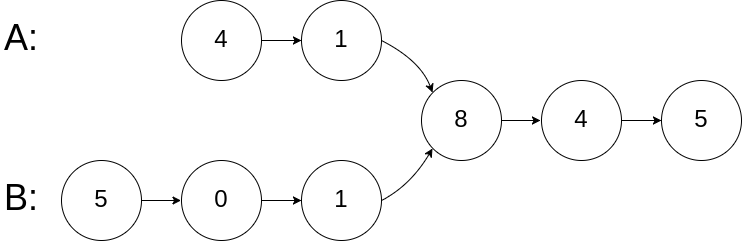
示例 1:
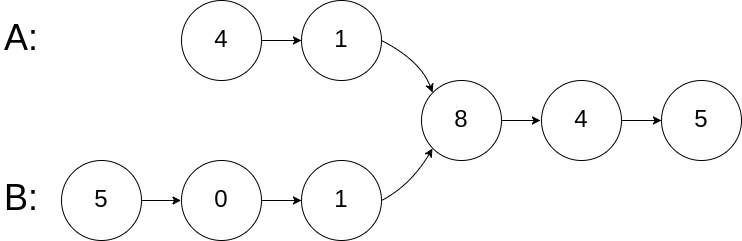
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出:Reference of the node with value = 8
输入解释:相交节点的值为 8 (注意,如果两个列表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,0,1,8,4,5]。在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
示例 2:
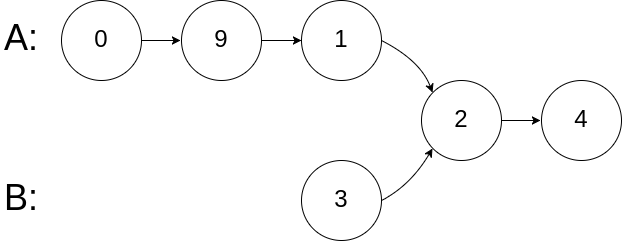
输入:intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出:Reference of the node with value = 2
输入解释:相交节点的值为 2 (注意,如果两个列表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [0,9,1,2,4],链表 B 为 [3,2,4]。在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例 3:
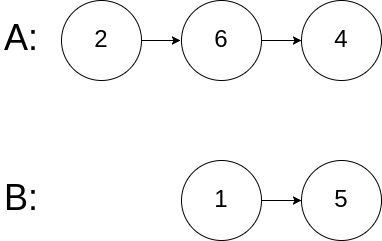
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出:null
输入解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。
解释:这两个链表不相交,因此返回 null。
注意:
如果两个链表没有交点,返回 null.
在返回结果后,两个链表仍须保持原有的结构。
可假定整个链表结构中没有循环。
程序尽量满足 O(n) 时间复杂度,且仅用 O(1) 内存。
分析:很到位
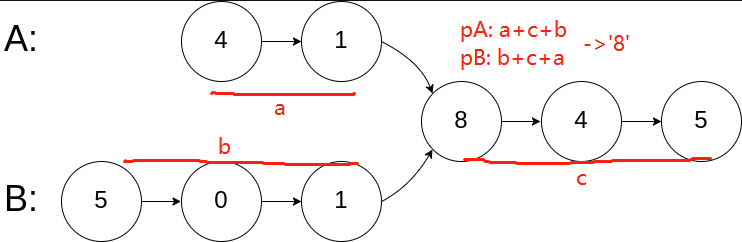
初始化 pA = headA, pB = headB,开始遍历。
以上图为例,pA会先到达链表尾,当pA到达末尾时,重置pA为headB;同样的,当pB到达末尾时,重置pB为headA。当pA与pB相遇时,必然就是两个链表的交点。(来个动态脑图,一目了然)
为什么要这样处理?因为这样的一个遍历过程,对pA而言,走过的路程即为a+c+b,对pB而言,即为b+c+a,显然a+c+b = b+c+a,这就是该算法的核心原理。
即使两个链表没有相交点,事实上,仍然可以统一处理,因为这种情况意味着相交点就是null,也就是上图中的公共部分c没有了,从而递推式变成了pA: a+b,pB: b+a,这同样是成立的。
code:
class Solution(object): def getIntersectionNode(self, headA, headB): ha, hb = headA, headB while ha != hb: ha = ha.next if ha else headB hb = hb.next if hb else headA return ha
7. 用栈实现队列
使用栈实现队列的下列操作:
push(x) -- 将一个元素放入队列的尾部。
pop() -- 从队列首部移除元素。
peek() -- 返回队列首部的元素。
empty() -- 返回队列是否为空。
示例:
MyQueue queue = new MyQueue();
queue.push(1);
queue.push(2);
queue.peek(); // 返回 1
queue.pop(); // 返回 1
queue.empty(); // 返回 false
说明:
你只能使用标准的栈操作 -- 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。
假设所有操作都是有效的 (例如,一个空的队列不会调用 pop 或者 peek 操作)。
分析:
挺简单的,注意逻辑要严密。
class MyQueue: def __init__(self): """ Initialize your data structure here. """ self.A = [] self.B = [] def push(self, x: int) -> None: """ Push element x to the back of queue. """ self.A.append(x) def pop(self) -> int: """ Removes the element from in front of queue and returns that element. """ if self.empty(): return if len(self.B) == 0: while len(self.A) != 0: self.B.append(self.A.pop()) return self.B.pop() else: return self.B.pop() def peek(self) -> int: """ Get the front element. """ if self.empty(): return if len(self.B) == 0: while len(self.A) != 0: self.B.append(self.A.pop()) return self.B[-1] else: return self.B[-1] def empty(self) -> bool: """ Returns whether the queue is empty. """ if len(self.B)==0 and len(self.A)==0: return True else: return False