int maximalSquare(vector<vector<char>>& matrix) { int height=matrix.size(); if(height==0) return 0; int width=matrix[0].size(); vector<vector<int>> vec(height,vector<int>(width,0)); int result=0; for(int i=0;i<height;i++) { for(int j=0;j<width;j++) { if(matrix[i][j]=='1') { vec[i][j]=1; if(i>0&&j>0) vec[i][j]+=min(min(vec[i-1][j],vec[i][j-1]),vec[i-1][j-1]); } result=max(result,vec[i][j]); } } return result*result; }
本题是动态规划的题目,vec[i,j]记录的是以matrix[i,j]为右下角的所能构成的正方形区域的边长的最大值。
递推公式,vec[i][j] = 1 + min(min(vec[i-1][j],vec[i][j-1]),vec[i-1][j-1]),计算的是当前单元格的“左”、“上”、“左上”三个单元格的最小值,再+1。
补充一个python的实现:注意i和j的值在matrix和dp中表示位置不同。
1 class Solution: 2 def maximalSquare(self, matrix: 'List[List[str]]') -> 'int': 3 m = len(matrix) 4 if m == 0: 5 return 0 6 n = len(matrix[0]) 7 dp = [[0 for _ in range(n+1)]for _ in range(m+1)] 8 res = 0 9 for i in range(m): 10 for j in range(n): 11 if matrix[i][j] == '1': 12 dp[i+1][j+1] = min(min(dp[i][j+1],dp[i+1][j]),dp[i][j]) + 1 13 res = max(res,dp[i+1][j+1]) 14 return res * res
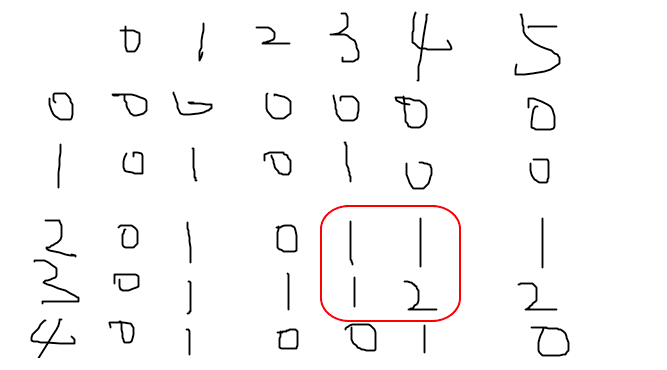
例如:对于输入测试样本,当遍历到红色的数字1时(i=2,j=3)
1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0
当i=2 j=3时,dp[3][4]的值是:dp[2][3]、dp[2][4]、dp[3][3]这三个位置的最小值1,再加上1。因此dp[3][4] = 1 + 1 = 2(即下图中的红色方框区域的计算)。
按照次递推公式计算,可得到如下二维数组dp: