1. 单源最短路问题 (Bellman-Ford 算法)
Bellman_Ford
单源最短路是固定一个起点,求它到其他所有点的最短路问题。
记从起点 s 出发到顶点 i 的最短距离为 d[ i ],则有等式成立:
d[ i ] = min{ d[ j ] + (从 j 到 i 的边的权值) | e = (j, i) ∈ E }
如果给定的图是一个DAG,就可以利用这条递推关系计算出 d。但是如果图中有圈,就无法这样计算。
记当前到顶点 i 的最短路长度为 d[ i ], 并设初值 d[ s ] = 0, d[ i ] = INF, 再不断使用递推式更新 d 的值, 就可以算出新的 d。只要图中不存在负圈(总长度小于0的有向环路),这样的更新操作就是有限的。结束之后 d 就是所求最短距离。
// 从顶点 from 指向顶点 to 的权值为 cost 的边 struct edge{ int from; int to; int cost; }; edge es[MAX_E]; int d[MAX_V]; //最短距离 int V, E; //求解从 s 出发到所有点的最短距离 void shortest_path(int s) { for (int i = 0; i < V; i++) d[i] = INF; d[s] = 0; while(true) { bool update = false; for (int i = 0; i < E; i++) { edge e = es[i]; if (d[e.from ] != INF && d[e.to ] > d[e.from ] + e.cost ) { d[e.to ] = d[e.from ] + e.cost; update = true; } } if (!update) break; } }
如果在图中不存在从 s 可达的负圈, 那么最短路不会经过同一顶点两次(也就是说最多通过 | V | - 1 条边),while(true) 最多执行 | V | - 1 次,因此复杂度是0(| V | * | E |)。反之,如果存在从 s 可达的负圈,那么在第| V | 次循环中也会更新 d 的值, 因此可用这个性质来检查负圈。如果一开始对所有顶点 i, 都把 d[ i ] 初始化为0,那么可以检查出所有的负圈。
// 如果返回 true 则存在负圈 bool find_negative_loop() { memset(d, 0, sizeof(d)); for (int i = 0; i < V; i++) { for (int j= 0; j < E; j++) { edge e = es[j]; if(d[e.to] > d[e.from] + e.cost) { d[e.to] = d[e.from] + e.cost; // 如果第 n 次仍然更新了,则存在负圈 if (i == V - 1) return true; } } } return false; }
SPFA(Shortest Path Faster Algorithm)
这是基于Bellman-Ford 的思想,采用先进先出(FIFO)队列进行优化的一个计算单源最短路的快速算法。
只要最短路径存在,SPFA算法必能求出最小值。我们假定最短路一定存在,即图中没有负权圈,所以每个结点都有最短路径值。每次入队的点的d【】值都在变小,在达到最短路径后,算法结束。
如果最短路径不存在时,即存在负圈,并且起点可以到达负圈,那么利用SPFA会进入死循环,因为d【】值会越来越小,无限循环,使得算法无法退出。若不存在负圈,则任何最短路上的点必定小于等于 | V |,换言之,我们用 vis[ i ] 来记录这个点入队的次数,所有的 vis[ i ] <= | V |,如果vis[ i ] > | V |,则表明这个图存在负圈。
复杂度:0(| V || E |)
struct edge{ int to; int cost; }; vector<edge> G[MAX_V]; int d[MAX_V]; //最短距离 int vis[MAX_V]; //节点i被访问的次数 bool inq[MAX_V]; //表示结点i是否在队列中 bool SPFA(int s) { memset(d, INF, sizeof(d)); memset(vis, 0, sizeof(vis)); memset(inq, false, sizeof(inq)); queue<int> q; q.push(s); d[s] = 0; inq[s] = true; while (!q.empty()) { int v = q.front(); q.pop(); inq[v] = false; if (vis[v]++ > V) return true; //判断是否存在负圈,如果存在则返回true for (int i = 0; i < G[v].size(); i++) { edge e = G[v][i]; if (d[e.to] > d[v] + e.cost ) { d[e.to] = d[v] + e.cost; if (!inq[e.to ]) { inq[e.to] = true; q.push(e.to); } } } } return false; }
这里参考自:
2.单源最短路问题(Dijkstra 算法)
让我们来考虑一下没有负边的情况。在 Bellman-Ford算法中,如果d[ i ] 还不是最短距离的话,那么即使进行 d[ j ] = d[ i ] + (从 i 到 j 的边的权值的更新),d[ j ]也不会变成最短距离。而且即使d[ i ] 没有变化, 每次循环也要检查一遍从 i 出发的所有边。这显然是浪费时间的。因此对算法做如下修改。
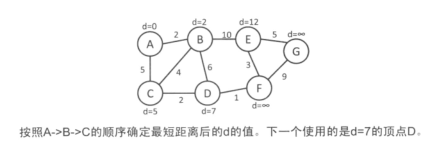
(1) 找到最短距离已经确定的顶点,从它出发更新相邻顶点的最短距离。
(2) 此后不需要再关心(1)中的最短距离已经确定的点。
那么怎么确定这个顶点?在最开始的时候,只有起点的最短距离是确定的,而在尚未使用的顶点中,距离 d[ i ] 最小的顶点就是最短距离已经确定的顶点。这是因为由于不存在负边,所以 d[ i ]不会在之后的更新中变小。
int cost[MAX_V][MAX_V]; //cost[u][v]表示边 e = (u,v)的权值,不存在是为INF int d[MAX_V]; //顶点s出发的最短距离 bool used[MAX_V]; //已经使用过的图 int V; //求从起点s出发到各顶点的最短距离 void dijkstra(int s) { fill(d, d + V, INF); fill(used, used + V, false); d[s] = 0; while(true) { int v = -1; //从尚未使用的顶点中选择一个距离最小的顶点 for (int u = 0; u < V; u++) if (!used[u] && (v == -1 || d[u] < d[v]))
v = u; if (v == -1) break; used[v] = true; for (int u = 0; u < V; u++) d[u] = min(d[u], d[v] + cost[v][u]); } }
使用邻接矩阵实现的话复杂度为0(| V |2).使用邻接表的话,更新最短距离只需要访问每条边一次即可,因此这部分的复杂度为0(| E |)。但每次都要枚举所有的顶点来查找下一个使用的顶点,因此最终复杂度仍为0(| V |2)。需要优化的是数值的插入(更新)和取出,使用堆可以解决。把每个顶点当前的最短距离用堆来维护。而每次从堆中取出的最小值就是下一次要使用的顶点。这样堆中的元素共有0(| V |)个,更新和取出数值的操作有0(| E |)次,因此整个算法复杂度为0(| E | log | V |)。
struct edge { int to; int cost; }; typedef pair<int, int> P; //first 是最短距离, second是顶点的编号 int V; vector<edge> G[MAX_V]; int d[MAX_V]; void dijkstra(int s) { //通过指定greater<P> 参数,堆按照first从小到大排序 priority_queue<P, vector<P>, greater<P> > q; fill(d, d + V, INF); q.push(P(0, s));
d[s] = 0; while (!q.empty()) { P p = q.top(); q.pop(); int v = p.second; if (d[v] < p.first) continue; for (int i = 0; i < G[v].size(); i++) { edge e = G[v][i]; if (d[e.to] > d[v] + e.cost) { d[e.to ] = d[v] + e.cost; q.push(P(d[e.to], e.to)); } } } }
相对于Bell-Ford的0(| V | | E |)的复杂度,Dijkstra算法的复杂度是0(| E | log | V |)更高效,但是在图中存在负边的情况下,Dijkstra就无法正确求解,还是需要用Bell-Ford算法。
这里可能会对SPFA和dijkstra+heap优化产生混淆,提供一篇非常清晰的辨别博客:
eg :POJ-2387

#include<iostream> #include<cstdio> #include<algorithm> #include<vector> #include<cstring> #include<queue> using namespace std; const int MAX_V = 10101; int INF = 0x3f3f3f3f; struct edge { int to; int cost; }; typedef pair<int, int> P; //first 是最短距离, second是顶点的编号 int V; vector<edge> G[MAX_V]; int d[MAX_V]; int T, N; void dijkstra(int s) { //通过指定greater<P> 参数,堆按照first从小到大排序 priority_queue<P, vector<P>, greater<P> > q; fill(d, d + V, INF); q.push(P(0, s)); d[s] = 0; while (!q.empty()) { P p = q.top(); q.pop(); int v = p.second; if (d[v] < p.first) continue; for (int i = 0; i < G[v].size(); i++) { edge e = G[v][i]; if (d[e.to] > d[v] + e.cost) { d[e.to ] = d[v] + e.cost; q.push(P(d[e.to], e.to)); } } } } int main() { cin >> T >> N; V = N; for (int i = 0; i < T; i++) { int p; edge e, ee; cin >> p >> e.to >> e.cost ; ee.to = p - 1; e.to -= 1; ee.cost = e.cost; G[p - 1].push_back(e); G[e.to].push_back(ee); } //cout << endl; /*for (int i = 0; i < N; i++) { for (int j = 0; j < G[i].size(); j++) cout << i << ' ' << G[i][j].to << ' ' << G[i][j].cost << endl; }*/ dijkstra(0); //for (int i = 0; i < N; i++) cout << d[N - 1] << endl; return 0; }
POJ-3268
这题大意是给你有向图,求每个点到 X 的最短路径 + X 到每个点的最短路径(原路径都不能使用),求出需要的最长时间
思路:第一遍用dijkstra 算法, 第二次只要把图反转即 cost[ i ][ j ] = cost[ j ][ i ],再使用dijkstra一次即可。当然 每个点到X的最短路也就是X到每个点的最短路(估计就我一个人不这么想)

#include<iostream> #include<cstring> using namespace std; int cost[1010][1010]; int d[1010]; bool vis[1010]; int ans[1010]; int V, E, X; int INF = 0x3f3f3f3f; void dijkstra(int s) { fill (d, d + V, INF); fill (vis, vis + V, false); d[s] = 0; while (true) { int v = -1; for (int i = 0; i < V; i++) if (!vis[i] && (v == -1 || d[i] < d[v])) v = i; if (v == -1) break; vis[v] = true; for (int i = 0; i < V; i++) d[i] = min(d[i], d[v] + cost[v][i]); } for (int i = 0; i < V; i++) ans[i] += d[i]; } int main() { cin >> V >> E >> X; //fill(cost[0], cost[0] + V * V, INF); memset(cost, INF, sizeof(cost)); for (int i = 0; i < E; i++) { int a, b, c; cin >> a >> b >> c; cost[a - 1][b - 1] = c; } dijkstra(X - 1); for (int i = 0; i < V; i++) for (int j = i; j < V; j++) // 这里我写成了 for(int j = 0; j < V)..这样会又改回来 swap(cost[i][j], cost[j][i]); dijkstra(X - 1); int maxs = 0; for (int i = 0; i < V; i++) maxs = max(maxs, ans[i]); cout << maxs << endl; }
POJ-2066
这题就是把家到附近城市的距离设置为0, 一遍Dijkstra就可以了 。但是这些题最坑的是 居然有重边。

因为草儿的家在一个小镇上,没有火车经过,所以她只能去邻近的城市坐火车(好可怜啊~)。 Input 输入数据有多组,每组的第一行是三个整数T,S和D,表示有T条路,和草儿家相邻的城市的有S个,草儿想去的地方有D个; 接着有T行,每行有三个整数a,b,time,表示a,b城市之间的车程是time小时;(1=<(a,b)<=1000;a,b 之间可能有多条路) 接着的第T+1行有S个数,表示和草儿家相连的城市; 接着的第T+2行有D个数,表示草儿想去地方。 Output 输出草儿能去某个喜欢的城市的最短时间。 Sample Input 6 2 3 1 3 5 1 4 7 2 8 12 3 8 4 4 9 12 9 10 2 1 2 8 9 10 Sample Output 9

#include<iostream> #include<vector> #include<queue> #include<algorithm> #include<cstdio> #include<utility> #include<functional> #include<cstring> using namespace std; typedef pair<int, int> P; const int MAX_V = 1005; int INF = 0x3f3f3f3f; int map[MAX_V][MAX_V]; int d[MAX_V]; int s[MAX_V], f[MAX_V]; bool used[MAX_V]; int T, S, D; void dijkstra(int s) { memset(d, INF, sizeof(d)); memset(used, false, sizeof(used)); //priority_queue<P, vector<P>, greater<P> > q; //q.push(P(0, s)); d[s] = 0; /*while (!q.empty()) { P p = q.top(); q.pop(); int v = p.second; if (d[v] < p.first) continue; for (int i = 0; i < MAX_V; i++) { if(map[v][i] == -1) continue; if (d[i] > d[v] + map[v][i]) { d[i] = d[v] + map[v][i]; q.push(P(d[i], i)); } } }*/ while(true) { int v = -1; for (int i = 0; i < MAX_V; i++) if (!used[i] && (v == -1 || d[i] < d[v])) v = i; if (v == -1) break; used[v] = true; for (int i = 0; i < MAX_V; i++) d[i] = min(d[i], d[v] + map[v][i]); } } int main() { while (~scanf("%d%d%d", &T, &S, &D)) { memset(map, INF, sizeof(map)); for(int i = 0; i < MAX_V; i++) map[i][i] = 0; //memset(d, INF, sizeof(d)); for (int i = 0; i < T; i++) { int a, b, c; scanf("%d%d%d", &a, &b, &c); if (c < map[a][b]) map[a][b] = map[b][a] = c; } for (int i = 0; i < S; i++) { scanf("%d", &s[i]); map[0][s[i]] = 0; map[s[i]][0] = 0; } dijkstra(0); for (int i = 0; i < D; i++) scanf("%d", &f[i]); int mins = INF; for (int i = 0; i < D; i++) mins = min(mins, d[f[i]]); printf("%d ", mins); } }
3.任意两点间的最短路问题(Floyd-Warshall 算法)
试用DP来解决。 记 d[ k + 1 ][ i ][ j ] 为在只使用 0 ~ k 个顶点下从 i 到 j 的最短路径长度。 当 k = -1 时我们认为只使用了 i 和 j 两个顶点,
所以d[ 0 ][ i ][ j ] = cost [ i ][ j ]. 接下来思考只使用顶点 0 ~ k 的问题归约到只使用 0 ~ k - 1 的问题上。
只使用 0 ~ k 时,我们 i 到 j 的最短路分两种情况:
(1)正好经过顶点 k 一次 。 d[ k ][ i ][ j ] = d[ k - 1 ][ i ][ k ] + d[ k - 1 ][ k ][ j ].
(2)完全不经过顶点 k 。 d [ k ][ i ][ j ] = d[ k - 1 ][ i ][ j ].
所以递推式为(如果使用同一个数组更新):
d[ i ][ j ] = min( d[ i ][ j ], d[ i ][ k ] + d[ k ][ j ] )
复杂度为0(| V |3),Floyd-Warshall 算法和 Bellman-Ford 算法一样,可以处理边是负数的情况。而判断图中是否有负圈,只需检查是否存在 d[ i ][ j ]是负数的顶点 i 就可以了。
int d[MAX_V][MAX_V]; int V; void floyd_warshall() { for (int k = 0; k < V; k++) for (int i = 0; i < V; i++) for ( int j = 0; j < V; j++) d[i][j] = min(d[i][j], d[i][k] + d[k][j]); }
如果复杂度在可接受的范围内,单源最短路径也可以用 Floyd-Warshall 进行求解。
4. 路径还原
以 Dijkstra 算法为例,试还原最短路径。 在求解最短路径时,满足 d[ j ] = d[ k ] + cost[ k ][ j ] 的顶点 k,就是最短路上的前驱节点,因此通过不断寻找前驱节点就可以恢复出最短路。复杂度为 0(| E |)。
此外,如果用 prev[ j ] 来记录最短路上顶点 j 的前驱,那么就可以在 0(| V |)的时间内完成最短路的恢复。 d[ j ] 被 d[ j ] = d[ k ] + cost[ k ][ j ] 更新时,修改 prev[ j ] = k,这样就可以得到 prev数组。在计算从 s 出发到 j 的最短路时,通过 prev[ j ] 就可以最短顶点 j 的前驱,因此不断把 j 替换成 prev[ j ]直到 j = s 为止就可以了。 其他两个算法类似。
int prev[MAX_V]; // 求从起点 s 出发到各个顶点的最短距离 void dijkstra(int s) { fill(d, d + V, INF); fill(used, used + V, false); fill(prev, prev + V, -1); d[s] = 0; while(true) { int v = -1; for (int u = 0; u < V; u++) if (!used[u] && (v == -1 || d[u] < d[v])) v = u; if (v == -1) break; used[v] = true; for (int u = 0; u < V; u++) if (d[u] > d[v] + cost[V][u]) { d[u] = d[v] + cost[v][u]; pre[u] = v; } } //到顶点 t 的最短路 vector<int> get_path(int t) { vector<int> path; for ( ; t != -1; t = prev[t]) // 不断沿着 prev[t] 走,直到 t = s path.push_back(t); // 翻转就是 reverse(path.begin(), path.end()); return path; } }
5. 例题
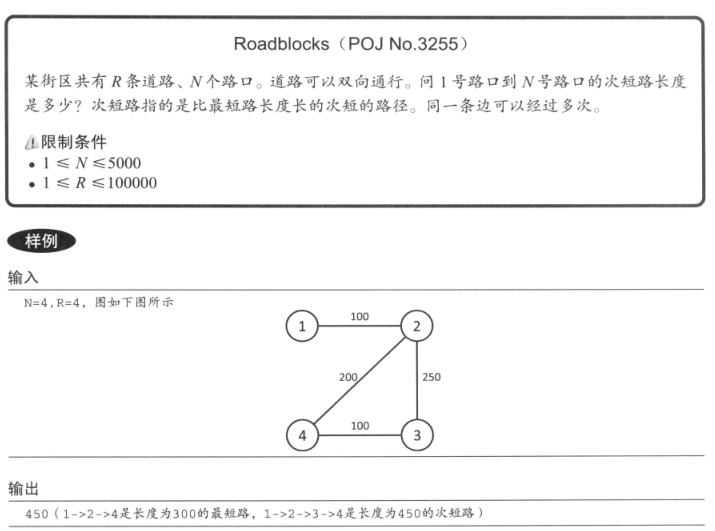
Dijkstra 算法的思路是依次确定尚未确定的顶点中距离最小的顶点,那么按照这个思路对算法进行少许修改就可以求出次短路。
到某个顶点 v 的次短路要么是到其它某个顶点 u 的最短路再加上 u -> v 的边, 要么就是到 u 的次短路再加上 u -> v 的边,因此所需要求的就是到所以顶点的最短路和次短路。因此我们不仅要记录最短距离,还要记录次短距离。接下来只要用与 Dijkstra 算法相同的做法,不断更新这两个距离就可以求出次短路。

typedef pair<int, int> P; struct edge{ int to; int cost; }; int N, R; vector<edge> G[MAX_N]; int dis[MAX_N]; // 最短距离 int dis2[MAX_N]; // 次短距离 void solve() { priority_queue<P, vector<P>, greater<P> > q; fill(dis, dis + N, INF); fill(dis2, dis2 + N; INF); dis[0] = 0; q.push(P(0, 0)); while (!q.empty()) { P p = q.top(); q.pop(); int v = p.second; int d = p.first ; if (dis2[v] < d) continue; for (int i = 0; i < G[v].size(); i++) { edge &e = G[v][i]; int d2 = d + e.cost; if (dis[e.to] > d2) { swap(dis[e.to], d2); q.push(P(dis[e.to], d2)); } if (dis2[e.to] > d2 && dis[e.to] < d2) { dis2[e.to] = d2; q.push(P(dis2[e.to], e.to)); } } } printf("%d ", dis2[N - 1]); }
