5. 完全数的求法

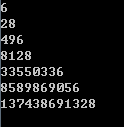
完全数（Perfect number），又称完美数或完备数，是一些特殊的自然数。它所有的真因子（即除了自身以外的约数）的和（即因子函数），恰好等于它本身。如果一个数恰好等于它的因子之和，则称该数为“完全数”。第一个完全数是6，第二个完全数是28，第三个完全数是496，后面的完全数还有8128、33550336等等。

梅森素数

　　古希腊数学家欧几里得在名著《几何原本》中证明了素数有无穷多个，并论述完全数时提出：如果2^P-1是素数(其中指数P也是素数)，则2^(P-1) * (2^P-1)是完全数。

#include<iostream>
#include<vector>
#include<algorithm>
#include<cmath>
#include<cstring>
using namespace std;
typedef long long ll;
int INF = 0x3f3f3f3f;
int prime[25] = {2,3,5,7,11,13,17,19,23};
bool is_prime(ll n) {
    for (int i = 2; (ll)i * i <= n; i++) 
        if (n % i == 0)
            return false;
    return true;
}

ll mod_pow(ll x, ll n, ll mod){
    if(n == 0) return 1;
    ll res = mod_pow(x * x % mod, n/2, mod);
    if(n & 1) res = res * x % mod;
    return res;
}

void solve() {
    for (int i = 0; i < 9; i++) {
        ll res = mod_pow(2, prime[i], INF);
        if (is_prime(res - 1)) {
            int x = prime[i] - 1;
            ll ans = mod_pow(2, x, INF);
            cout << ans * (res - 1)<< endl; 
        }
    }
}
int main() {
    solve();
}