本文主要讲述隐马尔科夫模及其在中文分词中的应用。 基于中文分词语料库,建立中文分词的隐马尔科夫模型,最后用维特比方法进行求解。
一、隐马尔科夫模型介绍
隐马尔科夫模型中包括两个序列,其中一个是观测序列,另一个是隐藏序列。模型要解决的一个问题是,给定观测序列, 求其对应的隐藏序列。比如对于语音识别,这里的观测序列是语音的每一个序列,隐藏序列是这一串语音对应的文字。 或者对于机器翻译,观测序列是待翻译的语言,而隐藏序列则是目标语言。在解决这类问题时,我们的已知条件是, 第一,隐藏序列中某一个元素到观测序列中某一个元素之间的映射关系。第二是隐藏序列中每个元素转变到另一个元素之间的关系。 并且会有两个假设,第一是每个隐藏元素中的元素,只依赖于它前面一个元素。第二是每一个隐藏元素能够直接确定另一个观测元素。 其中以上两个已知条件可以分别表示为两个矩阵,这个矩阵可以通过分词语料库,根据统计的方法求得。
从数学上理解,给定观测序列求解隐藏序列。一个观测序列可能对应无数个隐藏序列,而我们的目标隐藏序列就是, 概率最大的那一个隐藏序列,也就是说最有可能的那个序列。即求给定隐藏序列这个条件下观测序列概率最大的那个序列的条件概率问题。
虽然隐马尔科夫模型中做了比较强的假设,这里比较强的意思是,现实生活中,可能根本无法满足这种假设条件, 但是它的应用范围却是比较广泛,能够非常简单有效的解决复杂的问题。这个也是统计学方法的一个特点, 基于大量的数据,使用简单的方法便可以解决复杂的问题。这可能是大数据的一种威力吧,如果我们有足够多的数据, 那么我们的模型可以做简化。而如果我们只有少量的数据,则我们必须用非常精确的模型,才可以得到我们想要的结果。 数据模型以及数据量也是一种此消彼长的关系。
下图为隐马尔科夫模型的概率图,其中 (x) 代表隐藏序列, (y) 代表观察序列。
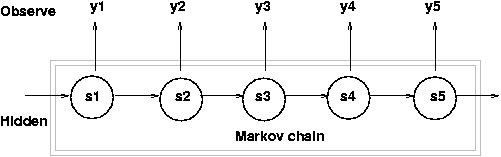
其中这里的隐藏序列,又称为一个马尔科夫链。马尔科夫链的定义是,序列中每一个元素,只依赖于他前面的一个元素而与其他所有元素不相关。
为了使用隐马尔科夫模型,我们必须知道两个矩阵。第一个矩阵式表示隐藏序列中, 一个元素转变到另一个元素的概率. 如果总的序列的元素数目为n,则这个是一个n乘n的矩阵。 第二个矩阵表示隐藏序列中某个元素转变到观测序列中某个元素的概率. 如果隐藏序列中元素个数为n,观测序列中元素的数目为m, 则这个矩阵的维数为n乘m。 这两个矩阵都可以通过大量的统计数据来求得。
第二、中文分词的隐马尔科夫模型
中文分词要解决的问题是,给定一段中文文字,将其划分为一个个单独的词或者单字。中文分词是所有后续自然语言处理的基础。 如果将连续的中文文字看作是观测序列,将每个文字所对应的分词状态看作是隐藏序列,每个字的分子状态可能有两个值, 一个表示这个字是某一个词的词尾,用字母E表示。另一个表示这个字不是某一个词的词尾,用字母B表示。 则中文分词问题可以看作是一个标准的隐马尔科夫模型。实际中将每个字的分子状态表示为四个可选的值。 词的开始,词的中间,词的结尾,单字成词。分别用bmes表示。
第三、中文分词语料库
在网上可以免费下载,北京大学和香港大学提供的中文分词语料库。这个语料库实际上是一个txt的文档, 文档中每个单独的词用两个空格隔开。 根据分词语料库,我们可以求得隐马尔科夫模型中的两个参数矩阵. 根据大数定理,概率等于次数的比值。因此为了模型的准确性, 我们必须有大量的语料数据来计算模型的参数。
第四、使用维特比算法进行求解
给定马尔科夫模型中的两个参数以及一个观测序列,求解隐藏序列的问题,可以看作是一个类似于图论中的最短路径问题.
维特比算法使用动态规划的方法进行求解。动态规划的子问题是,对于第 (i) 列的每一个元素 (A_j), 以这个元素为最后一个节点的最短路径。如果知道第 (i) 列的每一个元素的最短路径,那么第 (i+1) 列的每个元素的最短路径变可求得.
最终的结果就是第 (n) 列中每一个元素的最短路径中值最小的那一个元素所对应的最短路径。
第五、代码实现
a = 1
# print(a)
def foo(a):
return a+1
print("bbbb cccc ")