我经常在想,如果在标准的论文格式中,除了Abstract 和 Conclusion 以外,还必须加上一节 Key Idea,那该多好啊。事实上,对于我看过的大多数论文(虽然不算太多),都完全能够用一两段文字将其最基本的思想讲述清楚,余下所不能概括的通常也只是数学推导、实现细节和结果分析而已。或许这个概括应该包含在 Abstract 里,可惜大多数论文的摘要都太短而且千篇一律,只是提供了一些基本的信息以供收索引擎检索,或者供我们判断这篇文章的大概方向,实在对理解论文没有什么帮助,就像这样(图片来自www.phdcomics.com):

于是我们就不得不在完全摸不着头脑的情况下,老老实实的读完一大段的 Introduction,和 Previous Work,期望能找到一点感觉,但大多数情况是越看越迷糊。再到下一段,通常是要进入正题了,必较有良心的作者会在这里将整篇文章的中心思想略微提一下。比较无良的则是直接分节探讨细节,引入某某概念,推导某某公式,得出某某结果,再进行某某分析。而且大家都知道,在有些科技论文中向来都是有话不好好说的,比如长度不说长度,要说“Euclidean norm”,中位数不说中位数,要说“1/2th quantile value”,三线性插值不说三线性插值,要说“tensor product trivariate Bernstein polynomial of order
闲话扯完,言归正转。最近看了几篇有关屏幕空间全局光照明(Screen Space Global Illumination)的论文(好在大多数图形学领域的论文都还算是通俗易懂),在这里总结一下,做个备忘,省得以后想看第二遍的时后不用那么费力。
1. Reflective Shadow Maps
我们知道,场景中任意一点P所受到的辐照度可表示为一个级数:E_p = E_L + E_1 + E_2 + E_3+ …,其中 E_L 是来自光源的辐照度,E_i 是i-th bounce of indirect lighting。通常,取级数的前两项就已经能达到相当不错的效果,即 E_p = E_L+E_1。然而在实时渲染中,即使只想得到比较精确的E_L都极为困难,更别说E_1了。由此,Carsten Dachsbacher 等人提出了Reflective Shadow Map(RSM)来近似的计算E_1。RSM的基本思想如下:
1.1 建立Reflective Shadow Map
类似与Shadow Map,以光源为视点渲染整个场景,不同的是在每个像素点除了记录depth以外,还需要记录PN(Position & Normal)和辐射通量(radiant flux)。这样每个像素点就成了一个Pixel Light,最后得到的这些Buffers就称为Reflective Shadow Map。
这里比较关键的问题是怎么得到每个Pixel的辐射通量,以及辐射通量如何参与到E_1的计算。辐射通量即是intensity* solid angle,对于平行光源来说,可以认为每个像素都占有了相同的solid angle,因此辐射通量是一个常数。而对于聚光灯来说,越偏离主方向的像素占有的solid angle 越小,因此需要乘上一个 cosine 因子(如果考虑intensity的衰减,那么还要乘上相应的衰减因子)。最后需要存储的反射辐射通量,因此还要乘上一个反射系数。
如果假设是Lambertian表面话,根据辐射通量Φ和法线方向n,那么可以得到Pixel Light在任意方向ω的intensity:
注意,在原来论文中的公式是没有这个1/π 的,但在这里一方面为了保证物理上正确,另一方面为了方便理解,因此我又将1/π 加上去了,在实际实现时可以将1/π 折叠到辐射通量里面去,即存储Φ/π, 而不是Φ.
1.2 使用RSM
在渲染的时候怎么利用Reflective Shadow Map得到场景中任意一点x的E_1呢,首先将x投影到light space,得到在RSM中的参数坐标(s, t),在这里近似的采样RSM中位于点 (s, t) 附近的像素点作为pixel light set,若x点的法线为n,那么每个 pixel light (设为p)对点 x 贡献的辐射度为:
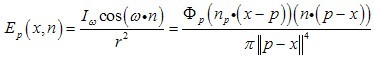
最后在所有的采样 pixel lights 上进行求和即得到 E_1(x)。
2. Splatting Indirect illumination
Splatting Indirect illumination 也是由Carsten Dachsbacher 提出的。在RSM中,E_1的计算是一个收集的过程(gathering),对每个场景点 x,都需要做大量的采样来收集附近的pixel lights 所贡献的 irradiance。而Splatting 是一个投射的过程(shooting)。首先在 RSM 中采样一定数量的 pixel lights,采样不一定是均匀分布的,比如在整体辐射通量比较高的地方可以采样更多的点(importance sampling)。然后每一个 pixel lights被当作一个 virtual point light(VPL),并投影到screen space。每一个VPL跟据它的flux和normal可以得到一个影响区域(比如可表现为screen space 中的一个矩形区域),并假设仅所有位于这个区域内的点受到此VPL的照明(也就是相当于将VPL的flux溅射(splat)在其整个影响区域中)。最后就是用 deferred shading的那一套进行光照计算即可。
3. Multiresolution splatting for indirect illumination
在Splatting 中,每个VPL都被限制在一个狭小的影响域里,而在Multiresolution splatting中则不设这样的限制,因此每个VPL都可以影响到整个screen。Multiresolution splatting的基本思想源于对以下事实的观察:由于indirect illumination通常是低频的,因此一个像素点点受到的照明情况以其相邻点受到的照明情况在大多数情况下都是非常接近的。基于这个观察,Multiresolution splatting首先将screen划分成为一个较低分辨率(比如16*16)的网格,每个格子称为一个subsplat。然后分别考查每一个subsplat,对于几何变化较小的subsplat来说,可以直接在这个低分辨率粒度下进行splatting,当计算完成后整个subsplat将得到相同的辐照度,这个结果已经足够。但是对于几何不连续的subsplat,则还需要进行进一步的划分(这就是为什么称为multiresolution splatting)。对于是否还进行进一步划分可以通过min-max mipmap来判断,这里需要建立四张mipmap,一张存depth,另外三张分别存normal的三个分量。每次划分将一个subsplat分成四个sub-subsplats, 然后再分成16个…就这样通过层次性地细化来完成整个的splatting过程。
4. Approximating Dynamic Global Illumination in Image Space
这个就不多说了,我上一篇已经做过介绍了,还给出了一个简单的实现。另,在本文中,所有的小节题目即是论文题目,有兴趣的同学请自行Google.com[.hk]。