AHOI/HNOI2017队长快跑

一道好题&难题

转化思想

SOL:

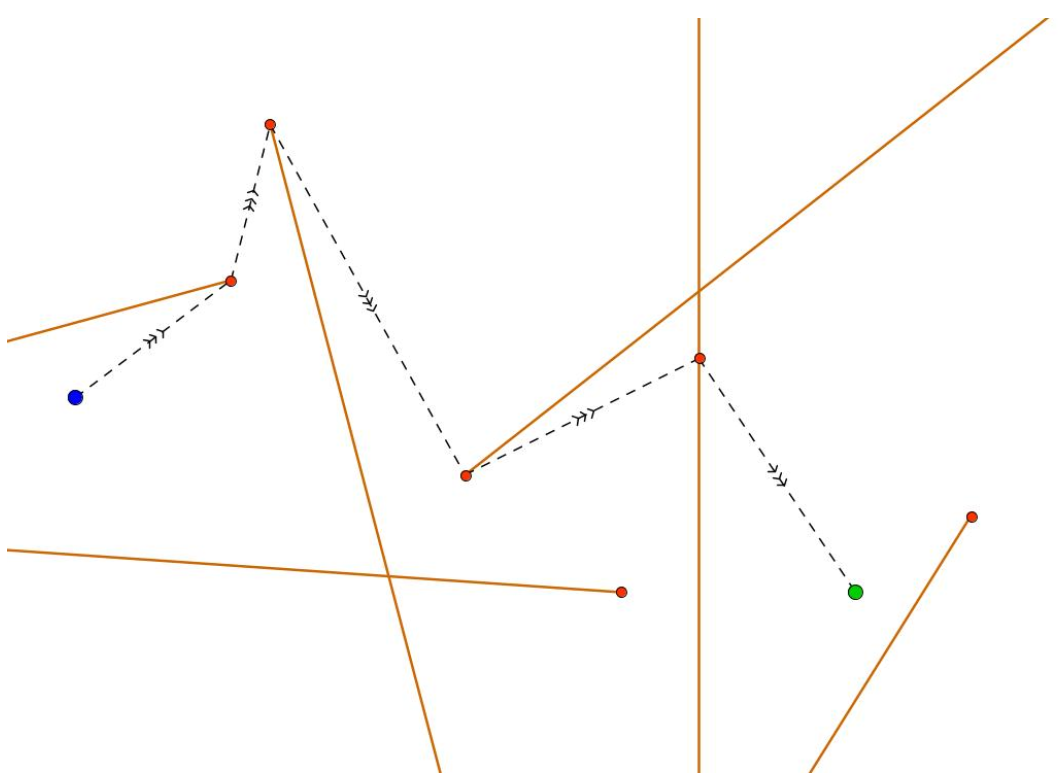
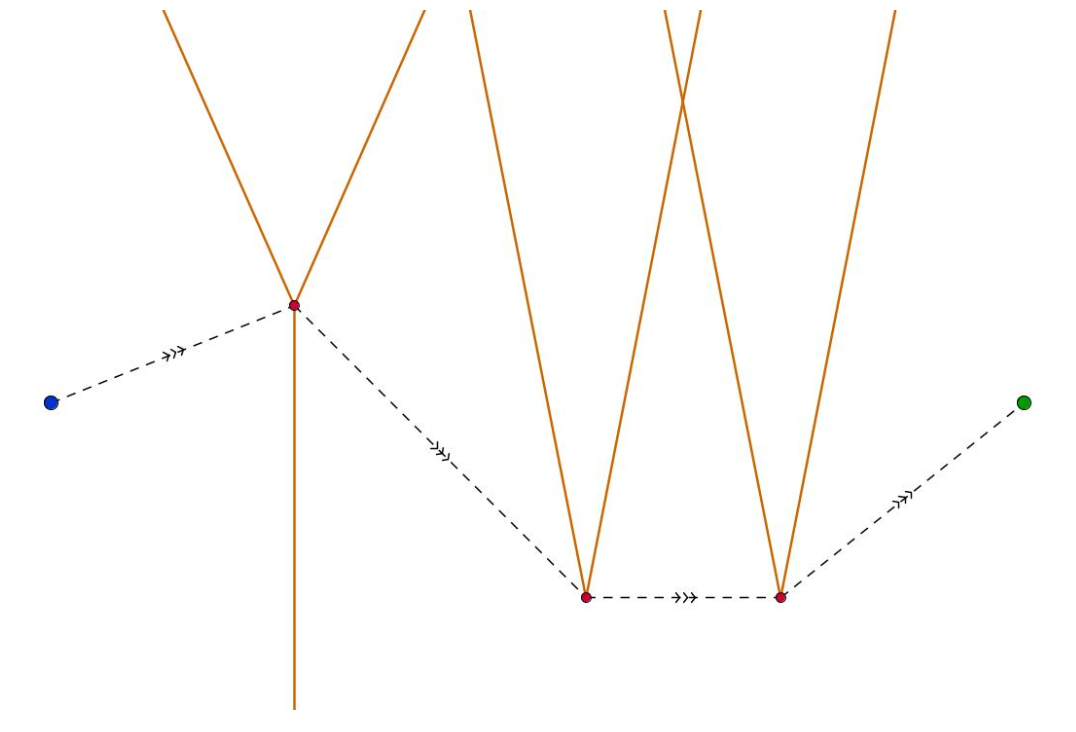
容易发现：我们一定沿着给出的点走动

我们可以把不同方向的线抽化为两个方向，上下

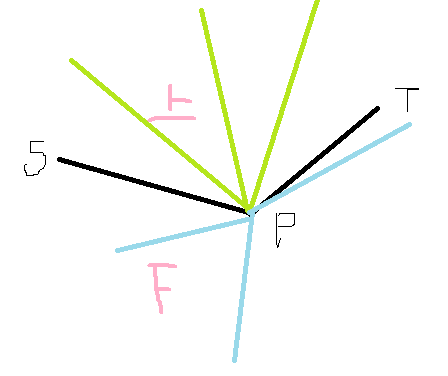
排序后，找到离自己最远的可以到达的点，即是最短（中途停留会变成折线，长度增长）

对每一个种建立单调队列

遇见这种情况，队首会被弹出，然后自己所在的单调队列就只剩下连线点和自己

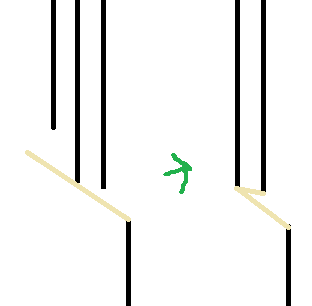
注:atan2返回值[-pi,pi]

#include<bits/stdc++.h>
using namespace std;
inline int read(){
	int x=0,f=1;char c=getchar();
	while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
	while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
	return f==1?x:-x;
}
const double pi=acos(-1.0);
const int N=1e6+4;
struct node{
	double x,y;int fl;
	node(double x=0,double y=0):x(x),y(y){}
	inline bool operator <(const node &a)const{
		return x<a.x;
	}
	inline node operator -(const node &a)const{
		return node(x-a.x,y-a.y);
	}
	inline double operator *(const node &a)const{
		return x*a.y-y*a.x;
	}
}p[N],a[N],s,t;
inline double dis(node a){
	return sqrt(a.x*a.x+a.y*a.y);
}
int n,m,q[2][N],ql[2],qr[2],from[N];
int main(){
	n=read();t.x=read();t.y=read();
	for(int i=1;i<=n;i++){
		static double l,r,th;
		p[i].x=read();p[i].y=read();scanf("%lf",&th);
		l=atan2(s.y-p[i].y,s.x-p[i].x);//返回值[-pi,pi] 
		r=atan2(t.y-p[i].y,t.x-p[i].x);
		if(l<r)p[i].fl=(l<th&&th<r);//1为下 
		else p[i].fl=!(r<th&&th<l);
	}
	sort(p+1,p+n+1);
	a[m=1]=s;
	for(int i=1;i<=n&&p[i].x<t.x;i++)
		if(p[i].x>s.x)a[++m]=p[i];
	a[++m]=t;
	q[1][0]=q[0][0]=1;
	for(int i=1,c,fl;i<=m;i++){
		c=a[i].fl;fl=(c?-1:1);
		int &l0=ql[c],&r0=qr[c],&l1=ql[c^1],&r1=qr[c^1],*q0=q[c],*q1=q[c^1]; 
		if(l1<r1&&(a[i]-a[q1[l1]])*(a[q1[l1+1]]-a[q1[l1]])*fl>=0){
			while(l1<r1&&(a[i]-a[q1[l1]])*(a[q1[l1+1]]-a[q1[l1]])*fl>=0)l1++;
			q0[l0=r0=r0+1]=from[i]=q1[l1];
		}
		else{
			while(l0<r0&&(a[i]-a[q0[r0-1]])*(a[q0[r0]]-a[q0[r0-1]])*fl>=0)r0--;
			from[i]=q0[r0];
		}
		q0[++r0]=i;
	}
	double ans=0;
	for(int i=m;i!=1;i=from[i])
		ans+=dis(a[i]-a[from[i]]);
	printf("%.10lf",ans);
	return (0-0);
}