围豆豆
游戏的规则非常简单,在一个N×M的矩阵方格内分布着D颗豆子,每颗豆有不同的分值Vi。游戏者可以选择任意一个方格作为起始格,每次移动可以随意的走到相邻的四个格子,直到最终又回到起始格。最终游戏者的得分为所有被路径围住的豆豆的分值总和减去游戏者移动的步数。矩阵中某些格子内设有障碍物,任何时刻游戏者不能进入包含障碍物或豆子的格子。游戏者可能的最低得分为0,即什么都不做。
注意路径包围的概念,即某一颗豆在路径所形成的多边形(可能是含自交的复杂多边形)的内部。下面有两个例子:
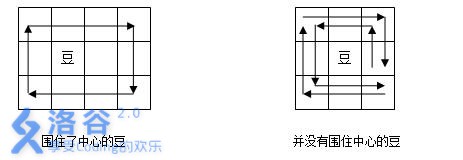
第一个例子中,豆在路径围成的矩形内部,所以豆被围住了。第二个例子中,虽然路径经过了豆的周围的8个格子,但是路径形成的多边形内部并不包含豆,所以没有围住豆子。
布布最近迷上了这款游戏,但是怎么玩都拿不了高分。聪明的你决定写一个程序来帮助他顺利通关。
题解
如何判断一个点在多边形内部?从这个点引一条射线不与多边形的任何顶点相交(这样的射线一定存在),若射线与多边形的边的交点有奇数个则在内部,否则在外部。
D 很小,考虑状压 DP。
预处理出豆子的坐标和每个状态 S 下所有豆子的得分和 sum[S]。
首先枚举一个起点 (x,y)。设 f[i][j][S] 表示走到了 (i,j) 这个格子,当前圈住的豆子的状态为 S 的最小边界长度。这个像斯坦纳树去掉子集枚举的部分。
然后,枚举状态 S。因为要走一条回路,所以用 sum[S]−f[x][y][S] 来更新答案。
SPFA 转移的时候处理 S 的方法有些奇特。首先自己要规定一个射线方向(水平或垂直),只有行动方向和它垂直的时候才考虑 S 是否变动。
不同方向的判定条件不一样,拜题目那个鬼畜的多边形围法所赐。
但无论如何,这个题比斯坦纳树有趣一些。
#include<bits/stdc++.h>
using namespace std;
template<class T> T read(){
T x=0,w=1;char c=getchar();
for(;!isdigit(c);c=getchar())if(c=='-') w=-w;
for(;isdigit(c);c=getchar()) x=x*10+c-'0';
return x*w;
}
template<class T> T read(T&x){
return x=read<T>();
}
#define co const
#define il inline
typedef long long LL;
int n,m,D,ans;
char ch[12][12];
int val[9],X[9],Y[9];
int sum[1<<9],f[12][12][1<<9]; // edit 1:12
struct node {int x,y,s;};
deque<node> q;
bool inq[12][12][1<<9]; // edit 1:12
co int dx[4]={1,-1,0,0},dy[4]={0,0,1,-1};
il int trans(int x,int nx,int y,int s){
for(int i=0;i<D;++i)if(y>Y[i])
if(x==X[i]&&nx==X[i]+1||x==X[i]+1&&nx==X[i]) s^=1<<i;
return s;
}
void solve(int x,int y){
memset(f,0x3f,sizeof f),f[x][y][0]=0;
q.push_back((node){x,y,0}),inq[x][y][0]=1;
while(q.size()){
int x=q.front().x,y=q.front().y,s=q.front().s;
q.pop_front(),inq[x][y][s]=0;
for(int i=0;i<4;++i){
int nx=x+dx[i],ny=y+dy[i];
if(ch[x][y]!='0') continue;
int ns=i<2?trans(x,nx,y,s):s;
if(f[nx][ny][ns]>f[x][y][s]+1){
f[nx][ny][ns]=f[x][y][s]+1;
if(!inq[nx][ny][ns])
q.push_back((node){nx,ny,ns}),inq[nx][ny][ns]=1;
}
}
}
for(int s=0;s<1<<D;++s)
ans=max(ans,sum[s]-f[x][y][s]);
}
int main(){
read(n),read(m),read(D);
for(int i=0;i<D;++i) read(val[i]);
fill(ch[0],ch[0]+m+2,'#');
for(int i=1;i<=n;++i){
scanf("%s",ch[i]+1);
ch[i][0]=ch[i][m+1]='#';
}
fill(ch[n+1],ch[n+1]+m+2,'#');
for(int s=0;s<1<<D;++s)
for(int i=0;i<D;++i)
if(s>>i&1) sum[s]+=val[i];
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j)
if('1'<=ch[i][j]&&ch[i][j]<='9')
X[ch[i][j]-'1']=i,Y[ch[i][j]-'1']=j;
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j)
if(ch[i][j]=='0') solve(i,j);
printf("%d
",ans);
return 0;
}