【线性筛】【质因数分解】【约数个数定理】hdu6069 Counting Divisors

d(x)表示x的约数个数，让你求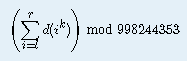（l,r<=10^12,r-l<=10^6,k<=10^7）

#include<cstdio>
using namespace std;
#define MOD 998244353ll
#define MAXP 1000100
typedef long long ll;
ll x,y;
int T,K;
bool isNotPrime[MAXP+10];
int num_prime,prime[MAXP+10];
void shai()
{
    for(long i = 2 ; i <  MAXP ; i ++)  
    {  
        if(! isNotPrime[i])  
            prime[num_prime ++]=i;  
        for(long j = 0 ; j < num_prime && i * prime[j] <  MAXP ; j ++)  
        {  
            isNotPrime[i * prime[j]] = 1;  
            if( !(i % prime[j]))  
                break;  
        }  
    }  
}
ll b[1000010],a[1000010];
int main(){
	scanf("%d",&T);
	shai();
	for(;T;--T){
		scanf("%lld%lld%d",&x,&y,&K);
		for(ll i=x;i<=y;++i){
			a[i-x+1ll]=i;
			b[i-x+1ll]=1;
		}
		for(int i=0;i<num_prime;++i){
			ll t=x/(ll)prime[i]*(ll)prime[i]+(ll)(x%(ll)prime[i]!=0)*(ll)prime[i];
			for(ll j=t;j<=y;j+=(ll)prime[i]){
				int cnt=0;
				while(a[j-x+1ll]%(ll)prime[i]==0){
					a[j-x+1ll]/=(ll)prime[i];
					++cnt;
				}
				b[j-x+1ll]=(b[j-x+1ll]*(((ll)cnt*(ll)K%MOD+1ll)%MOD))%MOD;
			}
		}
		ll ans=0;
		for(ll i=x;i<=y;++i){
			if((a[i-x+1ll]>1ll)){
				b[i-x+1ll]=(b[i-x+1ll]*((ll)K+1ll))%MOD;
			}
			ans=(ans+b[i-x+1ll])%MOD;
		}
		printf("%lld
",ans);
	}
	return 0;
}