数学女孩1 笔记

 知识点如下：

---

质因数分解定理。

算术基本定理，又称为正整数的唯一分解定理，即：每个大于1的自然数均可写为质数的积，而且这些素因子按大小排列之后，写法仅有一种方式。

因此，1不是质数。

给定一个正整数n，求n的所有约数的和。

首先进行质因数分解。

将正整数 n 进行质因数分解，一般都可以写成以下形式。假设p0,p1,p2,...,pm为质数，a0,a1,a2,...,am 为正整数，则有

n = p₀^a₀ * p₁^a₁ * p₂^a₂ * ... * p_m^a_m 

那么 n 的约数就可以表现为以下形式。

p₀^b₀ * p₁^b₁ * p₂^b₂ * ... * p_m^b_m 

此时，b0,b1,b2,...,bm 就是以下整数。

b₀=0,1,2,...,a0 中任意数

b₁=0,1,2,...,a1 中任意数

...

b_m=0,1,2,...,am 中任意数

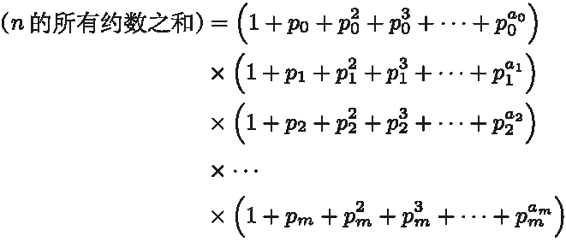
 起初没想到，但是确实可以这样写。

我想的是：m重循环，每个循环的循环次数是a_i+1次。遍历0,1,2,...,a_i，

其实是：为p₀，p₁，p₂，…，p_m各挑一个幂，乘起来，那么就可以如上图那样写。

括号内等比数列求和：

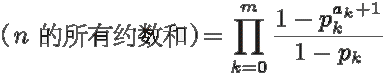
（完。）

好，上面给出了公式，先要进行质因数分解，然后代公式。

但是实际（编程）怎么做？似乎求出所有因数，然后再求和简单？