【Python 15】分形树绘制3.0（递归函数）

1.案例描述

 将递归函数与循环函数结合绘制2.0的图形

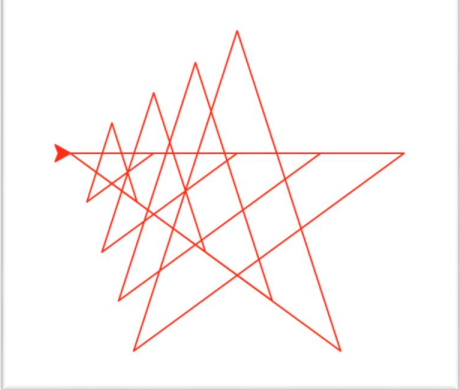
2.案例分析

 

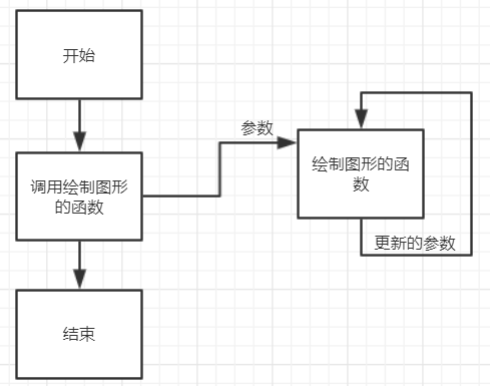
3.上机实验

"""
    作者：梁斌
    功能：五角星的绘制
    版本：3.0
    日期：03/08/2017
    新增功能：加入循环操作绘制重复不同大小的图形
    新增功能：使用迭代函数绘制重复不同大小的图形
"""
import turtle


def draw_pentagram(size):
    """
        绘制五角星
    """
    # 计数器
    count = 1
    while count <= 5:
        turtle.forward(size)
        turtle.right(144)
        # count = count + 1
        count += 1


def draw_recursive_pentagram(size):
    """
        迭代绘制五角星
    """
    # 计数器
    count = 1
    while count <= 5:
        turtle.forward(size)
        turtle.right(144)
        # count = count + 1
        count += 1

    # 五角星绘制完成，更新参数
    size += 10
    if size <= 100:
        draw_recursive_pentagram(size)


def main():
    """
        主函数
    """

    turtle.penup()
    turtle.backward(200)
    turtle.pendown()
    turtle.pensize(2)
    turtle.pencolor('red')

    size = 50
    draw_recursive_pentagram(size)

    turtle.exitonclick()

if __name__ == '__main__':
    main()

4.递归函数

递归(Recursion)是指在函数的定义中使用函数自身的方法。递归就是有去（递去）有回（归来）。

（1）递归三要素：

• 明确递归终止条件；

• 给出递归终止时的处理办法；

• 提取重复的逻辑，缩小问题规模。

（2）递归典型算法设计模型

• 在递去的过程中解决问题

function recursion(大规模){
    if (end_condition){      // 明确的递归终止条件
        end;   // 简单情景
    }else{            // 在将问题转换为子问题的每一步，解决该步中剩余部分的问题
        solve;                // 递去
        recursion(小规模);     // 递到最深处后，不断地归来
    }
}

• 在归来的过程中解决问题

function recursion(大规模){
    if (end_condition){      // 明确的递归终止条件
        end;   // 简单情景
    }else{            // 先将问题全部描述展开，再由尽头“返回”依次解决每步中剩余部分的问题
        recursion(小规模);     // 递去
        solve;                // 归来
    }
}

 Python实例（同时包含递去处理和归来处理）

# 树枝长度小于5时终止，每次树枝长度减少15（绘制右侧树枝后，原路返回到起点）
def draw_branch(branch_length):
    if branch_length < 5:
        return
    else:
        # 绘制右侧树枝
        turtle.forward(branch_length)
        print('向前 ', branch_length)
        turtle.right(20)
        print('右转 20')
        draw_branch(branch_length - 15)
       
        # 返回之前的树枝
        turtle.left(20)
        print('左转 20')
        turtle.backward(branch_length)
        print('向后 ', branch_length)

（3）递归与循环

• 递归与循环是两种不同的解决问题的典型思路，递归求解方式和循环求解方式往往可以互换。
• 递归可以很清晰地描述了一个问题的求解过程，比循环更容易理解。但递归涉及函数调用开销，常常会带来性能问题，所以效率会比循环要低。
• 建议在不影响程序的阅读的前提下，尽量使用循环，而不用递归。

 （4）递归使用场景（第三种最常见）

• 问题的定义是按递归定义的（Fibonacci函数，阶乘，…）；
• 问题的解法是递归的（有些问题只能使用递归方法来解决，例如，汉诺塔问题，…）；
• 数据结构是递归的（链表、树等的操作，包括树的遍历，树的深度，…）。

5.Pycharm技巧

（1）选中多行代码，Ctrl+l按一次注释，按两次取消注释。

（2）选中多行代码，Tab键缩行，Shift+Tab反向缩行。

（3）Alt + 上箭头，代码上移；Alt+下箭头，代码下移。

参考文档：

算法设计方法：递归的内涵与经典应用