TensorFlow实现的激活函数可视化

书上的代码：

# coding: utf-8

# In[1]:

import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from pylab import *


# In[19]:

def show_activation(activation,y_lim=5):
    x=np.arange(-10., 10., 0.01)
    ts_x = tf.Variable(x)
    ts_y =activation(ts_x )
    with tf.Session() as sess:
        init = tf.global_variables_initializer()
        sess.run(init)
        y=sess.run(ts_y)
    ax = gca()
    ax.spines['right'].set_color('none')
    ax.spines['top'].set_color('none')
    ax.spines['bottom'].set_position(('data',0))
    ax.spines['left'].set_position(('data',0))
    ax.xaxis.set_ticks_position('bottom')
    ax.yaxis.set_ticks_position('left')
    lines=plt.plot(x,y)
    plt.setp(lines, color='b', linewidth=3.0)
    plt.ylim(y_lim*-1-0.1,y_lim+0.1) 
    plt.xlim(-10,10) 

    plt.show()


# In[20]:

show_activation(tf.nn.sigmoid,y_lim=1)


# In[4]:

show_activation(tf.nn.softsign,y_lim=1)


# In[5]:

show_activation(tf.nn.tanh,y_lim=1)


# In[6]:

show_activation(tf.nn.relu,y_lim=10)


# In[7]:

show_activation(tf.nn.softplus,y_lim=10)


# In[8]:

show_activation(tf.nn.elu,y_lim=10)


# In[14]:

a = tf.constant([[1.0,2.0],[1.0,2.0],[1.0,2.0]])
sess = tf.Session()
print(sess.run(tf.sigmoid(a)))


# In[ ]:

sigmoid激活函数：

S(x)=1/(1+e^-x)

优点在于输出映射在0-1内，单调连续，适合做输出层，求导容易。

缺点在于软饱和性，即当x趋于无穷大时，一阶导数趋于0，容易产生梯度消失，神经网络的改善缓慢或消失。

softsign激活函数：

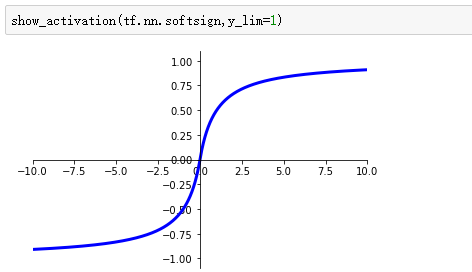
tanh激活函数：

tanh(x)=(1-e^-2x)/(1+e^-2x)

也具有软饱和性，收敛速度比sigmoid快，但是仍无法解决梯度消失的问题。

relu激活函数：

f(x)=max(x,0)

缺点：当relu在x<0时硬饱和，即在负半轴，激活函数的一阶导数等于0。

优点：由于x>0时导数为1，所以relu能在正半轴保持梯度的不衰减，缓解梯度消失的问题。

但是随着训练的进行，部分落入硬饱和区，权重无法更新。

softplus激活函数：

relu的平滑版本f(x)=log(1+exp(x))

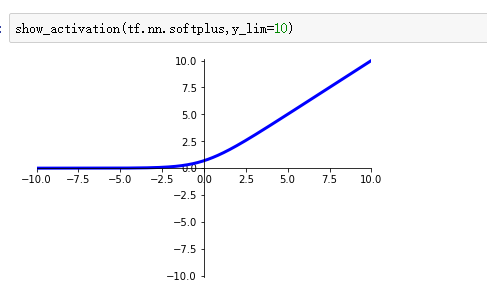
此外还有的激活函数如下数张图：

等等..............................................................................................

......................................................................................................

输入数据特征相差明显时，tanh效果较好，不明显时，sigmoid较好。二者在使用时需要对输入进行规范化，减少进入平坦区的可能。

relu是比较流行的激活函数，不需要输入量的规范化等...