学习率
认为尝试0.001以3倍网上增加算,进行测试。并让误差函数J的值越来越小才是正确的。
误差越来越大,可能是学习率过大造成,学习率太小可能导致梯度下降慢。
特征和多项式回归
线性回归不适合所有数据,有时候需要一些实际操作,如在房价问题中:
认为临街宽度,纵向深度作为特征,价格作为标签。但是在真正构建模型的过程中,面积才是实质上和价格挂钩,构建宽度和深度作为参数,不如使用面积作为参数的效果好。

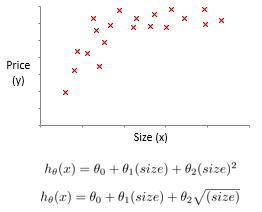
在监督的学习系统中进行的回归拟合,过程中只有一个面积参数,但是不同次数的函数式子,最后能够训练出的拟合效果也有差异。
该上图中,可以直观的看出,不少其他次方的函数进行拟合以后,比一次函数要好。
正规方程
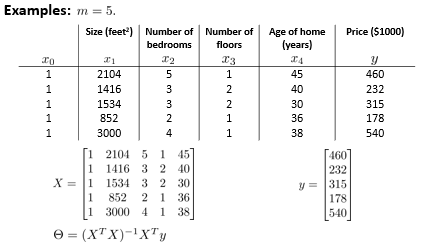
在如上的图中,m行数据,每行数据是一个条目,认为theta是特征feature n为5的一列数据。那么整个等式认为X * theta = Y


矩阵变化后的误差,可能由MSE(均方差)变为了SE(方差),其它不变,可以计算逆矩阵获得theta的值。
在计算过程中,矩阵求逆可能失败的原因至少有两点可以参考:
- 在该模型中的特征feature n中,存在相互关联的特征属性,导致特征之间存在恒等关系。
- 特征数量大于了数据条目。导致了求解参数theta的多解?
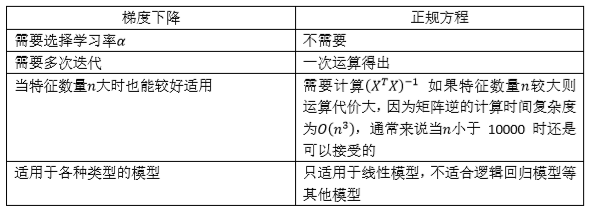
正规方程与梯度下降的参数求法的取舍
Octave说明
完全使用matlab
https://www.cnblogs.com/bai2018/p/10802800.html
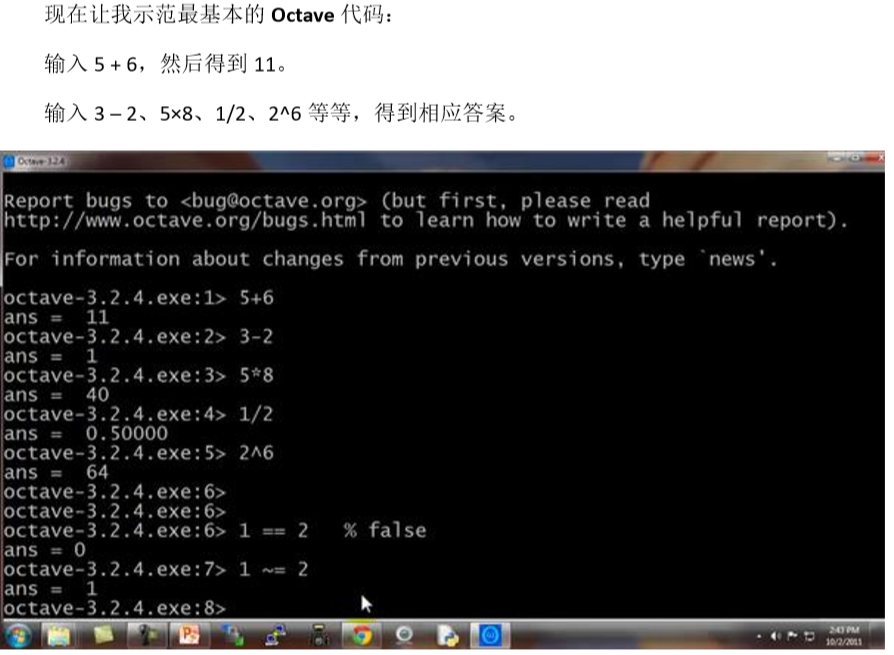


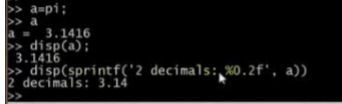



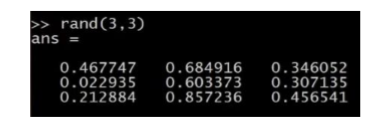


等等