行业轮动发展理论
根据产业链进行股市的划分,在上中下游进行利润和周期的排序,并根据发展规律,相关性排序,进行行业选择。
如下图是2017年到2020年11月的相关性,根据t分布计算出的行业行业相关置信度大于99%的行业。
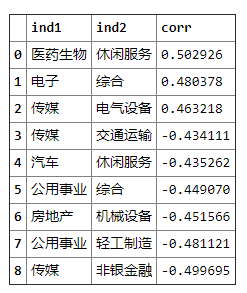
绩优成分股投资方法
从成分股选股,如沪深300
找出股息最高的10家
每年一次调仓。在2018-2020目前Alpha还在基准以上。
地址:https://uqer.datayes.com/labs/notebooks/6.4.1%E5%A4%A7%E5%B8%88%E7%B1%BB%E7%AD%96%E7%95%A51.nb
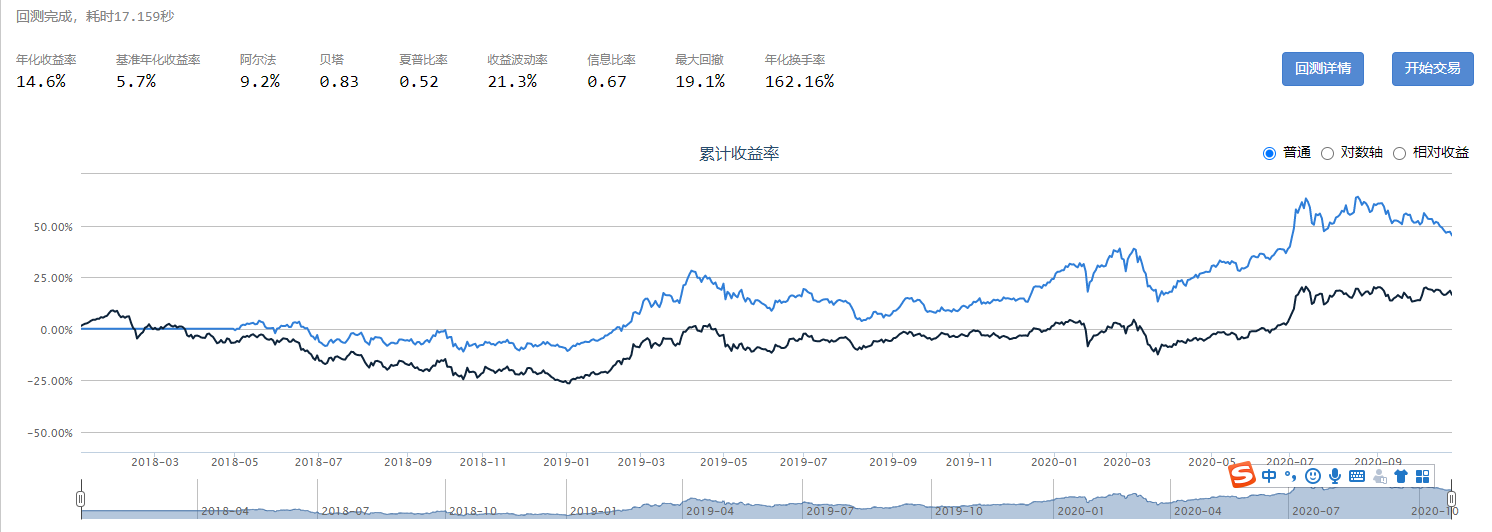
蓝筹股投资法
选股:同时满足类似以下的优质股条件:
股本大于市场均值,为成分股,大于10家基金公司持有,5年内3年净利润大于0,过去三年不间断派息,过去三年股息成长0.5倍,股息率大于4%。
调仓:
可以每年三次调仓即可。
效果一般,并没有获取良好的Alpha。
Smart Beta策略
Beta表示风险溢价的大小,Smart Beta采用不同的标准对选股信息进行评价。以下为近三年的测试数据,其中,删除线部分表示低于基准。
优化权重的方式评价进行选股。
根据权重:等权重选股,最小方差选股,平价选股,最大多元化选股。
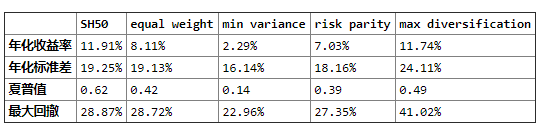
市盈率、市净率来构建价值因子,等权合成。
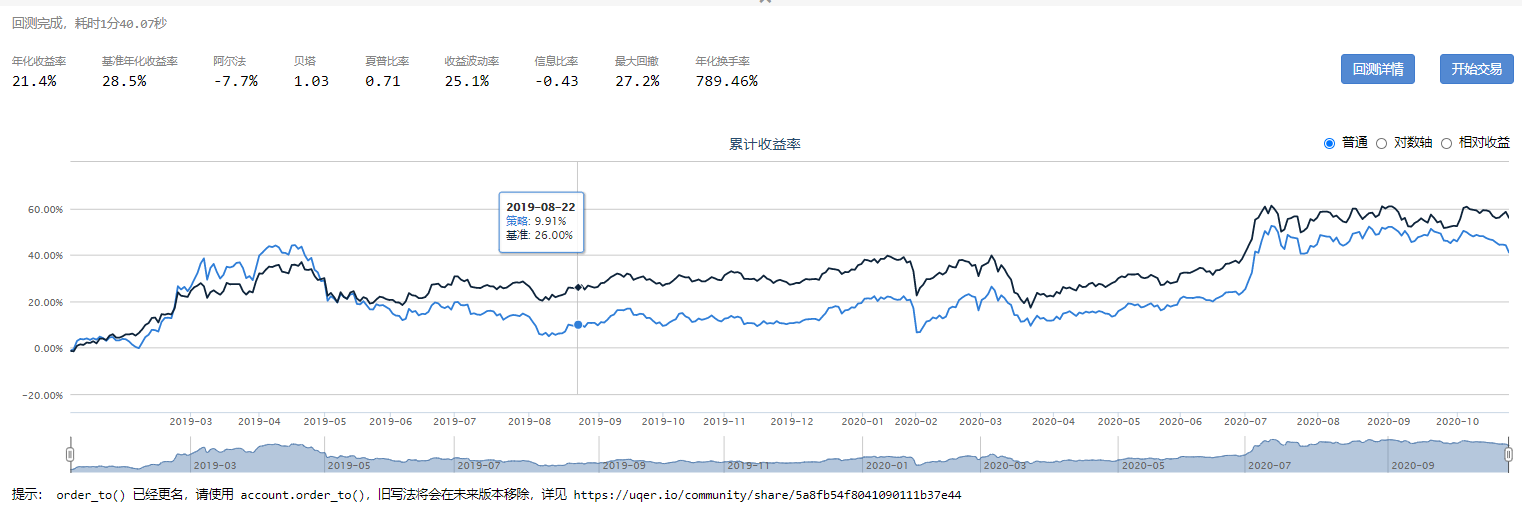
营业收入增长率、总资产增长率、归属于母公司所有者净利润增长率来构建成长因子,等权合成
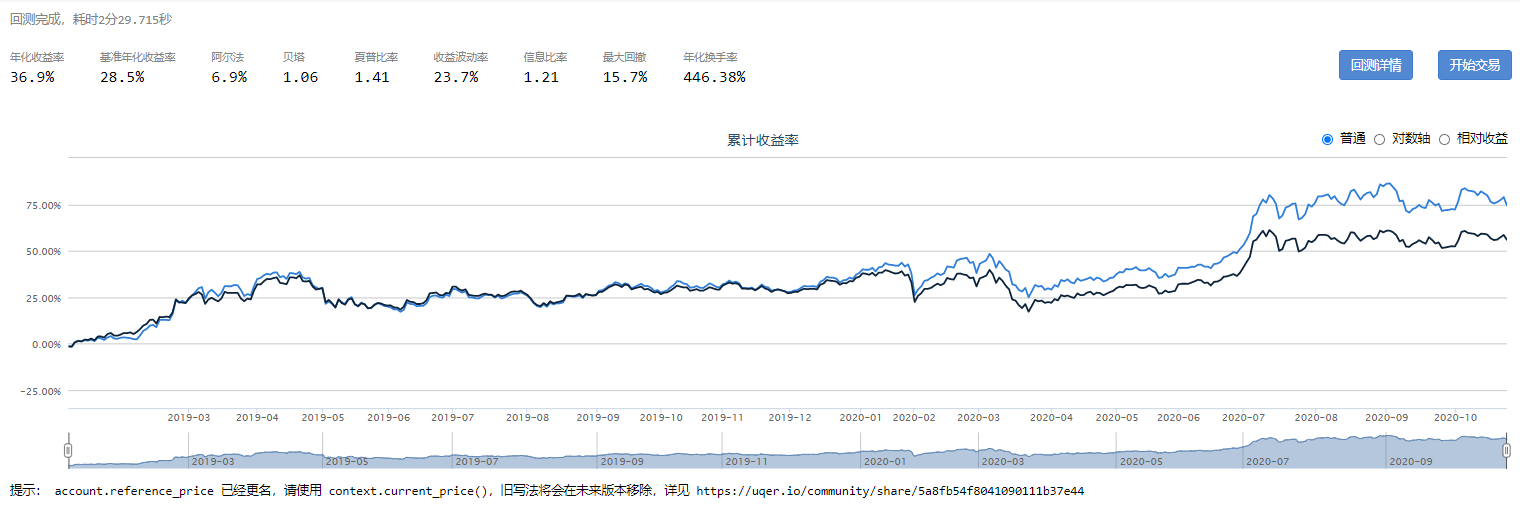
流动比率、营业利润率、权益收益率、总资产周转率来构建质量因子,等权合成
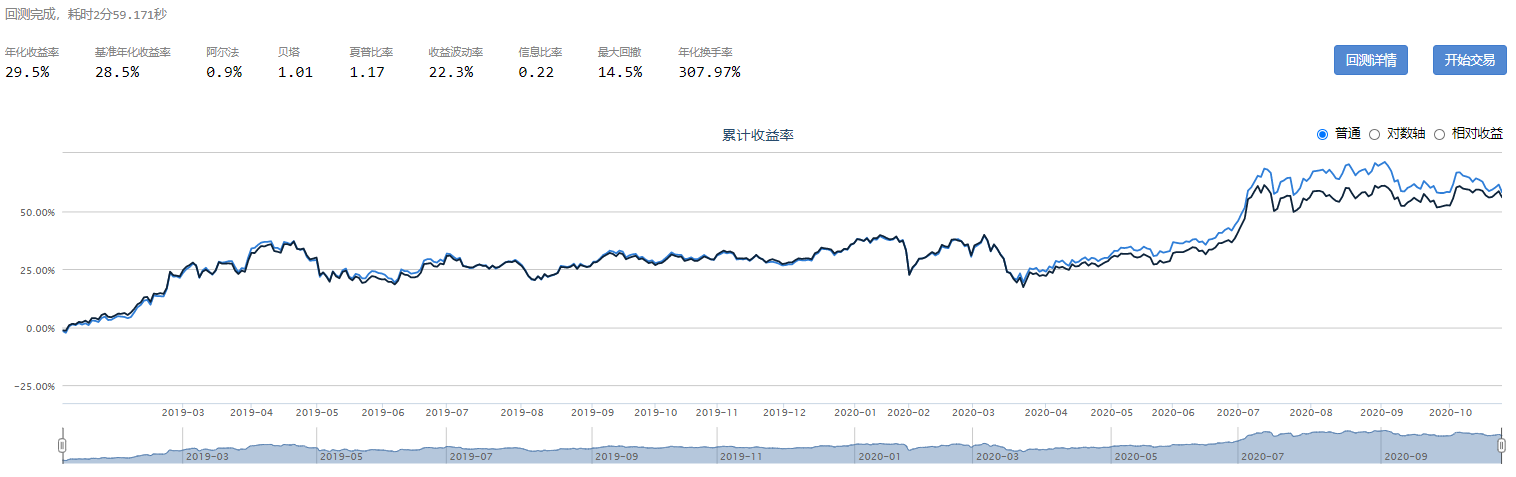
现金流市值比、5年平均现金流市值比来构建股息因子,等权合成
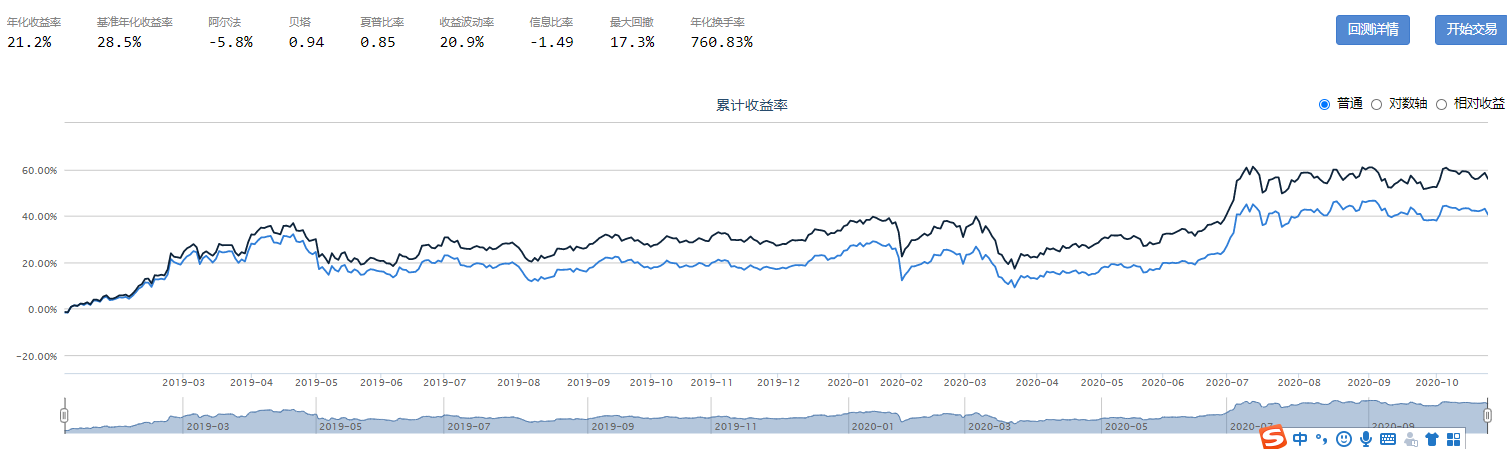
对数总市值来构建规模因子
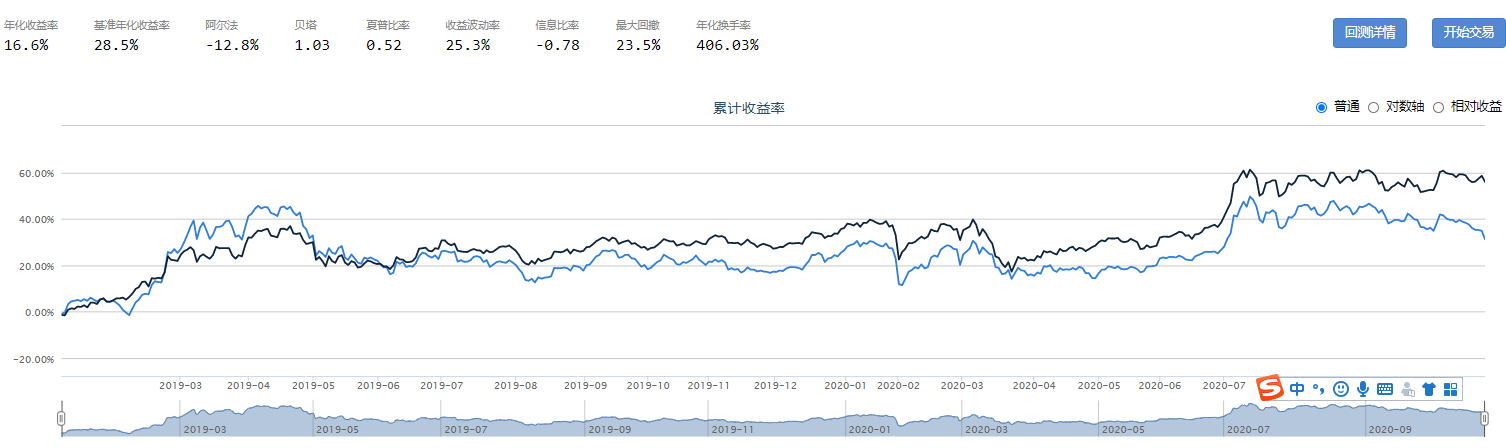
技术类指标策略
根据指标的变化进行投资
布林线指标BOLL
优矿平台提供的代码如下:
import numpy as np
import pandas as pd
start = '2019-01-01'
end = '2020-10-31'
benchmark = 'HS300'
universe = DynamicUniverse('HS300')
capital_base = 1000000
freq = 'd'
refresh_rate = 1
signalperiod = 9 # Signal平滑周期
accounts = {
'fantasy_account': AccountConfig(account_type='security', capital_base=10000000)
}
# 利用优矿的Signal框架来计算指标
# 优矿的BollUp和BollDown的参数是N=20, k=2,如果需要用到中轨,则直接使用MA20因子
def cross_situation(data, dependencies=['closePrice', 'BollUp', 'MA20', 'BollDown'], max_window=2):
cross = {}
for sec in data['closePrice'].columns:
# 收盘价上穿BOLL上轨
if data['closePrice'][sec][0] < data['BollUp'][sec][0] and data['closePrice'][sec][1] < data['BollUp'][sec][1]:
cross[sec] = 1
# 收盘价下穿BOLL中轨
elif data['closePrice'][sec][0] > data['MA20'][sec][0] and data['closePrice'][sec][1] < data['MA20'][sec][1]:
cross[sec] = -1
else:
cross[sec] = 0
return pd.Series(cross)
# 定义并注册Signal模块
def initialize(context):
up = Signal('BollUp')
down = Signal('BollDown')
cross = Signal('CRX', cross_situation)
context.signal_generator = SignalGenerator(up, down, cross)
def handle_data(context):
current_universe = context.get_universe(exclude_halt=True)
boll_up, boll_down, crx = context.signal_result['BollUp'], context.signal_result['BollDown'], context.signal_result['CRX']
buylist = []
account = context.get_account('fantasy_account')
cash = account.cash
current_positions = account.get_positions()
for stock in current_universe:
# 收盘价上穿BOLL上轨,且无持仓
if crx[stock] == 1 and stock not in current_positions:
buylist.append(stock)
# 收盘价下穿BOLL中轨,且有持仓
elif crx[stock] == -1 and stock in current_positions:
order_to(stock, 0) # 全部卖出
cash += current_positions[stock].amount * context.current_price(stock) # 估计买入金额
if len(buylist)==0:
weight = 0
else:
weight = min(1.0/len(buylist), 0.1) # 可以买入的股票数量,如果资金不够,只买入部分
for sec in buylist:
order_pct_to(sec, weight)
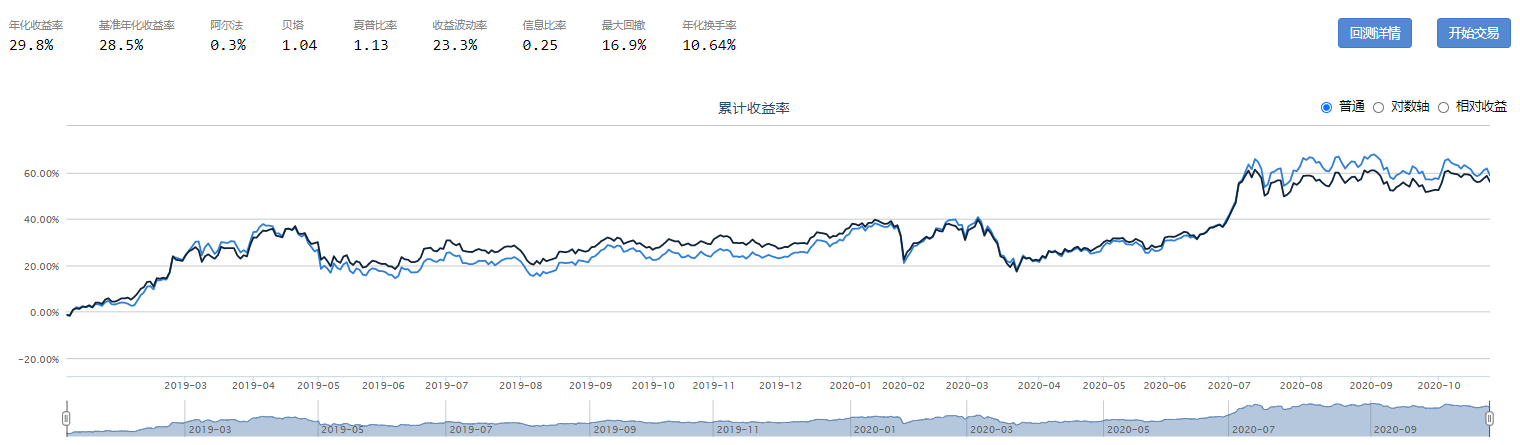
CII顺势指标
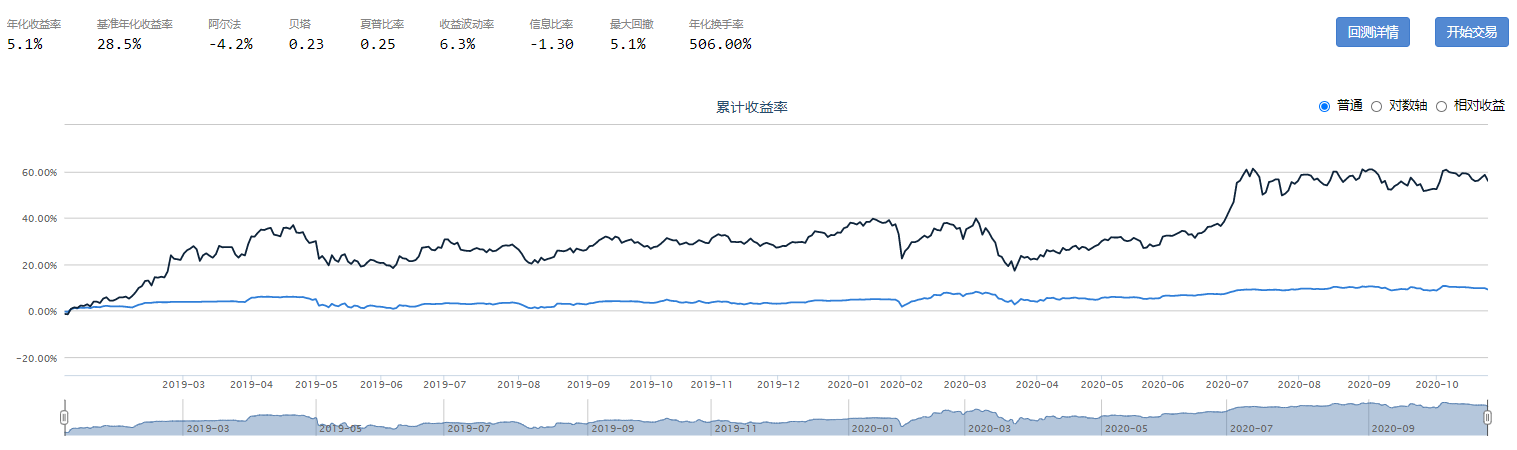
CMO动量摆动指标
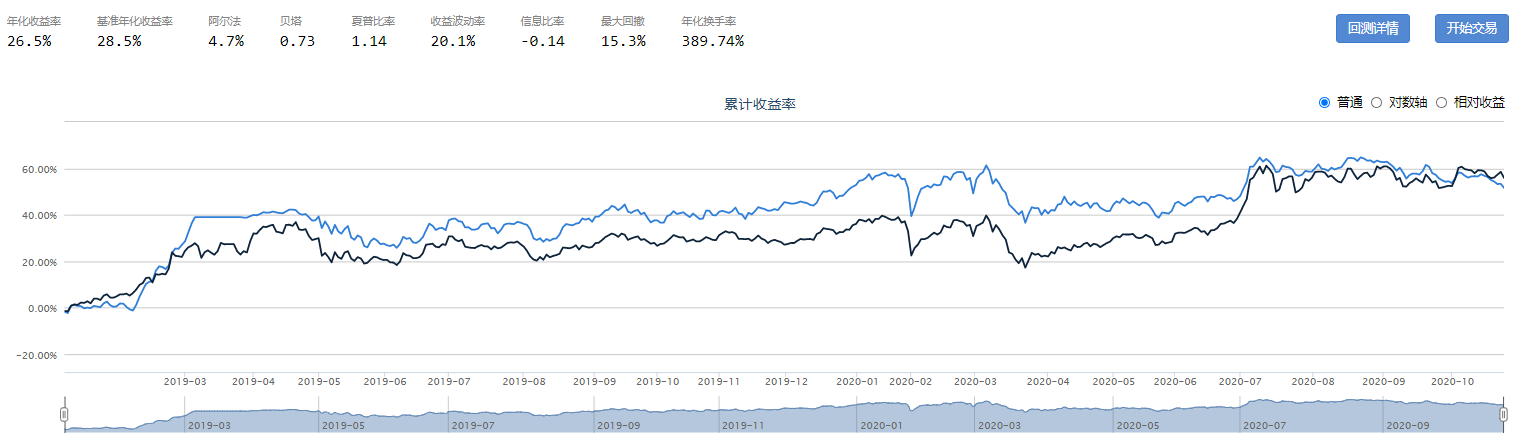
Chaikin Oscillator指标

资产配置方法
有效边界
投资者偏好
马科维茨均值方差模型最早提出将数理统计的方法应用到投资组合选择上,并将资产的期望收益率的波动率定义为风险。这种定义下,我们使用收益率的均值(E®)和标准差(σ®)来刻画 “收益”和“风险”。
通常,我们认为人们是“风险厌恶”的,并构造如下形式的效用函数来代表投资者的投资偏好: U®=E®- 1/2 Aσ^2 ® 其中E®表示投资组合的预期收益率,σ^2 ®表示投资组合的方差;
预期收益率越高,效用值越高,收益方差越大,效用值越小。
这表明投资者喜欢更高的E®,而不喜欢高的σ^2 ®。
由于不同的投资者对于风险和收益有不同的偏好,因此效用函数中加入风险厌恶系数参数A表示投资者不同偏好,A越大,则投资者为追求更高的收益愿意承担更大的风险,或者说该投资者要求更高的收益补偿面临的风险。
U同时是E和σ的函数,所以在σ-E图上,对于确定的A,不同的U表现为一组不相交的抛物线,这就是效用的无差异曲线,越往左上方的无差异曲线,代表越高的效用,因此投资者总是偏好位于左上方的无差异曲线上面的投资组合。
资产组合
假设有两种资产E_1和E_2,其预期收益率和方差分别为r_1、σ_1^2和r_2、σ_2^2,收益率相关系数为ρ。另有,r_1<r_2、〖0<σ〗_1<σ_2。如果同时投资于两种资产,权重分别为w_1、1-w_1,
则组合的期望收益率和方差可表示为: r=w_1 r_1+(1-w_1)r_2 σ^2= w_1^2 σ_1^2+〖(1-w_1)〗^2 σ_2^2+2w_1 (1-w_1)ρσ_1 σ_2 容易证明,当且仅当ρ=1时资产组合标准差与预期收益呈线性关系。
由于ρ的取值范围在-1和1之间,因此通常情况下σ^2= w_1^2 σ_1^2+〖(1-w_1)〗^2 σ_1^2+2w_1 (1-w_1 )ρσ_1 σ_2<〖(w_1 σ_1+(1-w_1 )σ_2)〗^2,即组合标准差小于两种资产标准差的加权平均,收益-标准差点在两种资产收益-标准差点连线的左侧。
甚至在大多数情况下,当把波动率更大的资产2开始引入组合时,其收益波动甚至比只投资于资产1时更小,当经过最小方差临界点时才会慢慢增大。
这也体现了投资组合的重要性——通过分散投资以更小的组合风险获得更高的收益。如下代码显示了当投资产品只有两种时,不同相关系数对应的不同有效边界。
有效边界和投资组合选择
当投资者面临的可选资产大于2种时,标准差和收益的关系就不仅仅局限于一条曲线了,通过权重的选取,投资者可选的收益-标准差点构成一个有边界的面。
人们趋利避险的心理决定了理性投资人在面临同样风险时,会选择预期收益率更高的组合;而在预期收益相同时,会选择风险较低的组合。
在所有可选的预期收益-标准差点中,位于最左侧的部分构成了一条边界线,其中从最小方差点往上的部分构成了有效边界。
在该边界线右下方的所有点是无效的投资组合,没有人会选择;在该边界线左上的所有点是不可能达到的投资组合。
Black-Litterman模型概述
基于马科维茨均值-方差模型的资产组合分析需要获取各类资产预期收益和方差。通常有两种方法可以用来得到预期收益和收益率方差的估计,情景分析法和历史数据法。
情景分析法主要根据当前行情和宏观经济环境等因素形成主观的预期,这种方法显然主观性、随意性过强。历史数据法则完全根据过去的历史收益率计算收益均值和方差,用来代替对未来的预期,这也是目前主流的做法。
这种做法存在几个问题,
一是历史数据往往由于历史的一些宏观环境或随机因素而存在比较大的波动性,这也意味着历史的收益率和方差在未来有可能由于宏观环境和随机因素的改变而不会重演;
二是根据采取的历史数据的时间段不同,估算出的预期收益率和方差也会有较大差别,从而导致得出的最优资产配置比例也会有较大差别。
高盛的Black F.和Litterman R.在其1991年的一篇论文中提到,在对全球债券投资组合的研究中,他们发现,当对德国债券预期报酬率做0.1%小幅修正后,该类资产的投资比例竟由原来的10.0%提高至55.0%。
这也意味着马科维茨的均值-方差模型得到的投资组合对于输入的参数过于敏感。 Black和Litteraman在前述均值方差模型的基础上,通过历史数据估计基准预期和方差,导入投资者主观预期,把历史数据法和情景分析法结合起来,形成新的市场收益预期,从而解决了前述模型中预期收益和方差估计中存在的问题。
B-L模型在均衡收益基础上通过投资者观点修正了期望收益,使得均值方差组合优化中的期望收益更为合理,而且还将投资者观点融入进了模型,在一定程度上是对马科维茨均值方差组合理论的改进。
B-L模型假设各资产收益率R服从联合正态分布,R~N(μ,Σ),其中μ和Σ是各资产预期收益率和协方差的估计值。现在假设估计向量μ本身也是随机的,且服从正态分布:μ~N(π,τΣ),其中π为先验期望收益率的期望值,通常由历史平均收益率表示。
模型引入投资者个人观点的方式是用线性方程组表示,每一个方程表示一个观点。例如,投资者认为未来第三种资产会比第一种资产收益率高2%,就可以表示为: -1×μ_1+0×μ_2+1×μ_3+⋯+0×μ_N=2% 投资者认为未来第二种资产收益率应该为5%,那么可以表示为: 0×μ_1+1×μ_2+0×μ_3+⋯+0×μ_N=5% 用P来表示该观点线性方程组的系数矩阵,观点方程组可表示为:Pμ = q。
由于投资人观点也存在不确定性,因此在q的基础上还可以加上一个随机误差项:Pμ = q+ ϵ,其中ϵ~N(0, Ω),因而Pμ~N(q, Ω)。这里,P被称为Pick Matrix,为K×N矩阵,表示对于N种资产的K个观点;
q为K×1看法向量;Ω为看法向量误差项的K×K协方差矩阵,表示投资者观点的不确定程度。通常对于Ω,采用Ω=diag(τPΣP^T)的方式构造。 前面我们讨论过市场的看法:μ~N(π,τΣ),用P调整后的市场看法可表示为:Pμ~N(Pπ,τPΣP^T)。
投资人观点和市场看法的差距服从分布:N(q-Pπ, Ω+τPΣP^T) 然后根据贝叶斯法则,结合先验信息和投资者观点,可以计算调整后的预期收益率和收益率方差分别为: Π ̂=Π+τΣP^T 〖(Ω+τPΣP^T)〗^(-1) (q-Pπ) M=τΣ-τΣP^T 〖(Ω+τPΣP^T)〗^(-1) PτΣ Σ_P=Σ+M 其中,Π为先验的期望收益,通过历史平均年化收益得到;
Π ̂为个人观点调整后的期望收益;Σ为资产收益率之间的协方差矩阵;M为后验分布预期收益率的方差;Σ_P为调整后预期收益率方差;τ为均衡收益方差的刻度值,体现了对个人观点在总体估计中的权重,通常取值在0.025~0.05; P、q、Ω为观点矩阵。
得到调整后的期望收益率和方差后,就可以根据马科维茨均值方差模型计算最优权重。
Black-Litterman模型应用 在实践中应用该模型,简要来说主要有如下步骤:
(1) 计算得到先验的期望收益; (2) 个人观点模型化,观点可以涉及单个资产,也可以有多个资产,最后按照一定的规则将所有观点构建成矩阵P、Q和Ω; (3) 计算调整后的预期收益率、调整后的收益率方差; (4) 根据调整后的期望收益,利用均值方差模型计算最优权重。 下面的代码提供了若干应用B-L模型进行优化的函数。
其中get_BL_efficient_frontier()用于获取根据调整后的收益率期望和方差得到的有效边界;draw_efficient_frontier()用于绘制有效边界图形;get_BL_minimum_variance_portfolio()用于获取最小方差投资组合;get_BL_maximum_utility_portfolio()用于获取基于给定效用函数的最大化效用投资组合;get_maximum_sharpe_portfolio()用于获取最大夏普率投资组合。