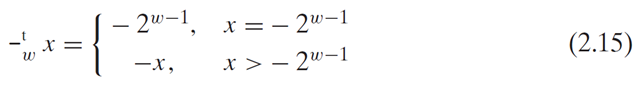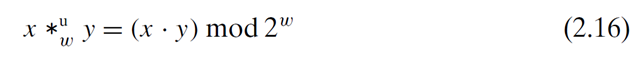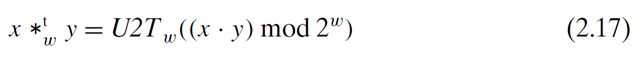Adding two positive integers can yield a negative result, and the comparation x<y can yield a different result with the comparation x-y<0. This properties are caused by the finite nature of computer arithmetic.
2.3.1 Unsigned Addition
Consider two nonnegative integers x and y, which are represented by w-bit unsigned numbers , s.t. .
Thus, , which need w+1 bits to represent the sum of x+y.
If we maintain the sum of x+y as w+1 bits, and add it to another value, we may need w+2 bits, and so on. So this infinite word size bits can not fully represent the results of this arithmetic operation. Note that, some other languages,as lisp can support infinite precision arithmetic.
In general, if , the leading bit in w+1-bit representation of the sum will be 0, and hence discarding it will not change the numeric value. While if
, the leading bit will be 1, and hence discarding it will be equivalent to substracting
from the sum.
Let define the operation for the arguments x and y such that
, so
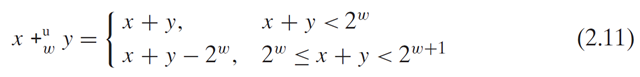This is precisely the result in C when adding two w-bit unsigned values.
In C programs overflows are not signaled as errors, The following method can determine whether overflow has occurred.
Supposed , we claim overflow occurrs when s<x, or equivalent s<y.
To see this clearly, if s did not overflow, we have surely , on the other hand, if s did oveflow we have
.
Let us define the value such that
,where
is an operation.
2.3.2 Two’s-Complement Addition
We can not use the modular addition for two's-complement addition. While most computers use the same instructions to perform either signed and unsigned addition.
Thus, we can define two's-complement addition for ，denoted as
on operands x and y such that
as
By equation 2.5, we can write , and
, and use the property that
is simply addition modulo
, then we have following derivation:
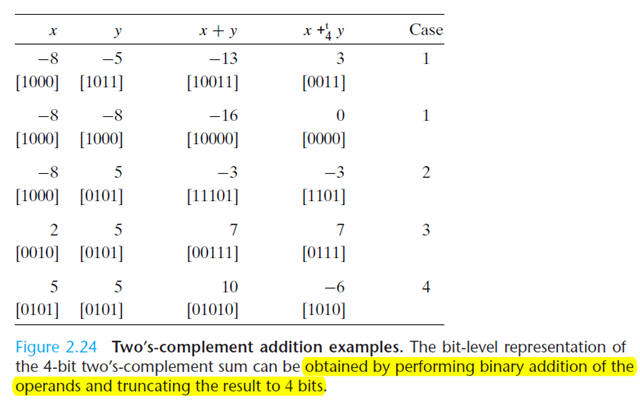
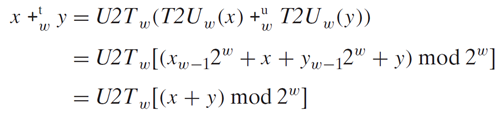The following figure illustrates this formula: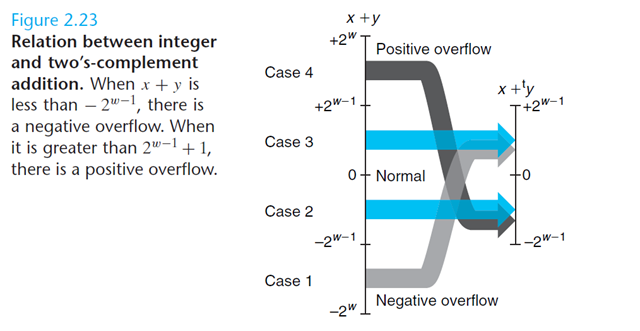
That is:
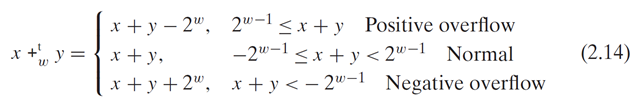This model is just from mathemetic sight. When the computer works, it actually truncates for w bits int particular data type size.
For the following example,
Equation also let us identify the cases where overflow has occurred. when both x and y are negative but xy>=0, we have negative overflow. when both x and y are positive but x
y<0, we have positive overflow.
2.3.3 Two’s-Complement Negation
For every number x in the range has a additive inverse under
:
Define the value such that
as
Bit-level representation of two’s-complement negation
1.One technique for performing two’s-complement negation at the bit level is to complement the bits and then increment the result. That is compute the –x and ~x+1 will give identical results. ( T2B(x) + T2B(~x+1) = 0 )
2. Another way is based on spiting the vector into two parts.
Let k be k-th position from rightmost, where first meet with the 1, so the bit-level representation of x has the form ,the negation is written in binary form
. (
+
= 0).
2.3.4 Usnsigned Multiplication
Define be the w-bit unsigned multiplication operation.
2.3.5 Two’s-Complement Multiplication
Define be the w-bit unsigned multiplication operation.
We claim that the bit-level representation of the product operation is identical for both unsigned and two’s-complement multiplication.