本章如果要归结成一个问题的话，可以归结为选择问题，比如要从一堆数中选择最大的数，或最小的数，或第几小/大的数等， 这样的问题看似很简单，似乎没有什么可研究的必要，因为我们已经知道了排序算法，运用排序+索引的方式不就轻松搞定了？但细想，排序所带来的时间复杂度是不是让这个问题无形之中变得糟糕。那算法研究不就是要尽可能避免一个问题高复杂度地解决，让那些不敢肯定有无最优解的问题变得不再怀疑，这也是算法研究者所追求的一种极致哲学。既然排序让这个问题解决的性能无法确定，那我们就抛开排序，独立研究问题本身，看有没有确定性的，且更优的解决之道，所以，这就是本章所探讨的问题。
一、中位数和顺序统计量
中位数：用非形式化的语言描述：中位数表示这样的一位数，它所属集合的“中点元素”。如果集合元素n为奇数，则中位数为(n+1)/2处；如果n为偶数，则中位数出现在n/2（下中位数）和n/2+1（上中位数）处，一般无特殊说明，我们都取下中位数。
顺序统计量：在一个n个元素组成的集合中，第i个顺序统计量是该集合中第i小的元素。
最大值：第1个顺序统计量。
最小值：第n个顺序统计量。
选择问题：给定一个包含n个元素的集合A和一个整数i，1<=i<=n，我们需要得到一个整数x，其中有i-1个元素小于它，即第i个顺序统计量。
前面说过，这个问题最直观的解法是通过排序+索引的方式，但排序算法有多种，且时间复杂度略高。我们需要更低时间复杂度来解决这个问题，要求线性时间，即O(n)。我们总结下算法导论上提出的方法，一步步展示如何O(n)来解决这个问题。
二、最大值、最小值
1、O(n)求最大值、最小值
这个采用最直观朴素的解法就能解决，我们取个名字吧，叫做“锦标赛法”。就是一个个比较，时间复杂度O(n)，已经没有比这更优的了。代码如下：
1 /***********线性时间求最小值************/ 2 int Minimun(int arr[], int n) 3 { 4 int nMin = arr[0]; 5 for(int i = 1; i < n; i++) 6 //min 7 if(nMin > arr[i]) 8 nMin = arr[i]; 9 //max 10 // if (nMax < arr[i]) 11 // nMax = arr[i]; 12 return nMin; 13 }
2、3/2n次比较同时求最大最小值
按照锦标赛法，同时求最大最小值，需要2(n-1)次比较，但是换一种思路，我们没必要一个元素比较两次，而是两个元素比较一次，然后得出大小关系，在分别和最大、最小值比较，这样两个元素就只用比较3次，总共就是3/2n次。这里要分奇偶数看待，但不管奇偶，都需要3/2n次。比较次数减少了，时间也就降低了。代码如下：
1 /***********通过3n/2次比较求最小值和最大值**********/ 2 void MinAndMax(int arr[], int n, int &nMin, int &nMax) 3 { 4 int i; 5 //如果n是奇数 6 if(n % 2 == 1) 7 { 8 //将最大值和最小值设置为第一个元素 9 nMin = arr[1]; 10 nMax = arr[1]; 11 i = 2; 12 } 13 //如果n是偶数 14 else 15 { 16 //将前两个元素作一次比较，以决定最大值怀最小值的初值 17 nMin = min(arr[1], arr[2]); 18 nMax = arr[1] + arr[2] - nMin; 19 i = 3; 20 } 21 //成对地处理余下的元素 22 for(; i < n; i=i+2) 23 { 24 //将一对输入元素互相比较 25 int a = min(arr[i], arr[i+1]); 26 int b = arr[i] + arr[i+1] - a; 27 //把较小者与当前最小值比较 28 if(a < nMin) 29 nMin = a; 30 //把较大者与当前最大值比较 31 if(b > nMax) 32 nMax = b; 33 } 34 }
3、最坏情况下，n-lgn-2次比较求第二小的元素（习题9.1-1）
本处要求的时间复杂度中含有lgn，我们自然想到这恰好是由n个元素组成的二叉树中的树的高度。有了这个提示之后，我们把思考点放在如何将n个元素的比较转化成一棵二叉树来求。通过前面的决策树，我们知道，决策树中的叶子节点，就是n个元素的排序组合，那么对应过来，我们可以得到n个元素恰好也可以成为二叉树的叶子节点，那么只需通过两两比较就可以得到，如下：
1）将n个元素两两分组，若为奇数，则单出一个；
2）比较每组元素得到最小值，将其作为该组两个元素的父亲节点；
3）对每组得到的父亲节点再采用1）的方式，直到最终剩余一个元素，即根节点。
这样，我们采用自底向上的方式构建了一棵二叉树，比如集合(2, 1, 4, 3, 5)，我们得到这样一棵树：
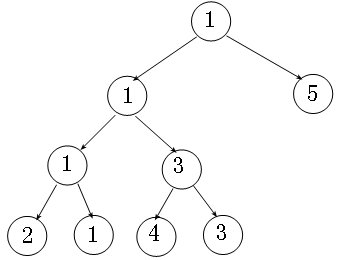
接下来，就是找第二小的元素，根节点是第一小的元素，我们从根节点往下遍历，就可以找到第二小的元素，如上图：第一次找到5，第二次3，第三次2，到达叶子节点，也就找到第二小的元素。现在我们来分析下时间复杂度：
1）自底向上比较建树需要n-1次比较；
2）自顶向下寻找需要lgn-1次比较（树高）;
所以，总的时间复杂度即为：n-1-lgn-1 = n-lgn-2，本题我们就不代码实现了，有兴趣的读者可以自己试试。
三、期望为线性时间的选择算法
一般选择问题看起来要比找最大、最小值要复杂得多，但令人惊奇的是，这两个问题的渐近运行时间却是相同的，都为O(n)。本节介绍的这个算法很强悍，期望的时间复杂度就能达到O(n)，但最坏情况下的时间复杂度却为O(n^2)。该算法采用的是快速排序章节中的Partition过程来得到划分的中点，如果该中点恰好等于选择的点，则即为所求，否则再在左右两个区间中用同样的方法再次寻找，伪代码如下：
RANDOMIZED-SELECT(A, p, r, i) 1 if p = r 2 then return A[p] 3 q ← RANDOMIZED-PARTITION(A, p, r) 4 k ← q - p + 1 5 if i = k ▹ the pivot value is the answer 6 then return A[q] 7 elseif i < k 8 then return RANDOMIZED-SELECT(A, p, q - 1, i) 9 else return RANDOMIZED-SELECT(A, q + 1, r, i - k)
实现代码如下：
1 //找两个数之间的随机数 2 int Random(int m, int n) 3 { 4 srand((unsigned)time(NULL)); 5 int nRet = m + rand()%(n - m + 1); 6 return nRet; 7 } 8 9 void Swap(int &m , int &n) 10 { 11 int t = m; 12 m = n; 13 n = t; 14 } 15 16 //找到适合的分区中点 17 int RandomPatition(int arr[], int p, int r) 18 { 19 int nRand = Random(p, r); 20 Swap(arr[r], arr[nRand]); 21 22 int nTemp = arr[r]; 23 24 //设置两个哨兵i,j从左遍历到右 25 int i = p - 1; 26 int j = p; 27 while (j < r) { 28 if (arr[j] <= nTemp) { 29 Swap(arr[i+1], arr[j]); 30 i ++; 31 } 32 j ++; 33 } 34 Swap(arr[i+1], arr[r]); 35 return i+1; 36 } 37 38 //寻找arr[p,r]中任意第k小的数 39 int RandomizedSelectMin(int arr[], int nLeft, int nRight, int nMin) 40 { 41 assert(nLeft <= nRight); 42 assert(nMin <= (nRight-nLeft+1)); //nMin start from 1,arr[] start from 0; 43 44 if (nLeft == nRight) 45 return arr[nLeft]; 46 47 int nMid = RandomPatition(arr, nLeft, nRight); 48 49 int k = nMid - nLeft + 1; 50 if (k == nMin) 51 return arr[nMid]; 52 53 else if (k > nMin) 54 return RandomizedSelectMin(arr, nLeft, nMid-1, nMin); 55 else 56 return RandomizedSelectMin(arr, nMid+1, nRight, nMin-k); 57 }
习题9.2-3要求实现一个非递归的版本，如下：
1 //非递归方法 2 int RandomizedSelect_NRecur(int arr[], int nLeft, int nRight, int nMin) 3 { 4 assert(nLeft <= nRight); 5 assert(nMin <= (nRight-nLeft+1)); //nMin start from 1,arr[] start from 0; 6 7 int nMid, k; 8 while(true) { 9 if (nLeft == nRight) 10 return arr[nLeft]; 11 12 nMid = RandomPatition(arr, nLeft, nRight); 13 14 k = nMid - nLeft + 1; 15 if (k == nMin) 16 return arr[nMid]; 17 else if (k > nMin) 18 nRight = nMid - 1; 19 else { 20 nLeft = nMid + 1; 21 nMin = nMin - k; 22 } 23 } 24 }
四、最坏情况下为线性时间的选择算法
前面说过，Randomized_Select在最坏情况下，时间复杂度为O(n^2)，这取决与划分的元素在集合中的位置。本节介绍的Select算法就能达到这样的要求，Select算法的思想是保证集合的划分是个好的划分，所以，需要对Partition做一点修改，具体的算法步骤如下：
（1）将输入数组的n个元素划分为n/5（上取整）组，每组5个元素，且至多只有一个组有剩下的n%5个元素组成。（为何是5，而不是其他数，有点不明白。） （2）寻找每个组织中中位数。首先对每组中的元素（至多为5个）进行插入排序，然后从排序后的序列中选择出中位数。 （3）对第2步中找出的n/5（上取整）个中位数，递归调用SELECT以找出其中位数x。（如果是偶数去下中位数） （4）调用PARTITION过程，按照中位数x对输入数组进行划分。确定中位数x的位置k。 （5）如果i=k，则返回x。否则，如果i<k，则在地区间递归调用SELECT以找出第i小的元素，若干i>k，则在高区找第(i-k)个最小元素。
如何保证是一个好的划分，该算法采用计算中位数的中位数的方法，首先将集合划分为5个元素一组的集合，不够5个元素的，单独做一个集合；然后采用插入排序找到5个元素的中位数，再从找到的中位数找到中位数，这样双重的中位数就能够保证这是一个较好的划分。但是为什么是5个元素一组，书中没特别说明，我想这是一个多次尝试的经验值，通过多个值测试时间复杂度之后，发现5是最好的。我们也可以具体分析一下：
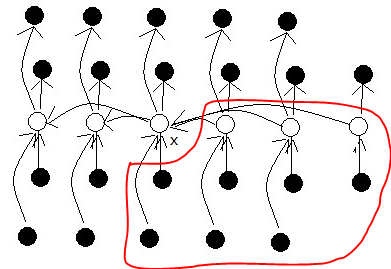如上图，至少有一半的组中有3个元素大于x，不算x所在组和元素不足5个的组，大于x的元素个数至少为：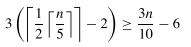
进而可以得到其递归式为：
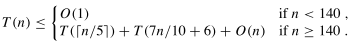
详细可见书上的推导，运用代入法，我们可以得到其时间复杂度为O(n)。
同理，我们可以分析当划分为7个元素一组时（习题9.3-1），递归式为：
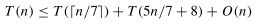
同样，时间复杂度也为O(n)。
当划分为3个元素一组时，递归式为：
其时间复杂度变为O(nlgn)，所以3不是好的划分，7相对5来说划分元素太多，不太适合应用，所以，最终定为5个元素划分为一组，是较好的选择！
根据上面算法的步骤，可以写出该算法的代码如下：
1 #include <iostream> 2 #include <cassert> 3 using namespace std; 4 5 void Swap(int &m , int &n); 6 int Partition(int arr[], int nLeft, int nRight, int nMedian); 7 int Find(int arr[], int nLeft, int nRight); 8 int Insert(int arr[], int nLeft, int nRight); 9 int Select(int arr[], int nLeft, int nRight, int nMin); 10 11 int Select(int arr[], int nLeft, int nRight, int nMin) 12 { 13 assert(nLeft <= nRight); 14 assert(nMin <= (nRight-nLeft+1)); 15 16 if (nLeft == nRight) 17 return arr[nLeft]; 18 19 int nMedian = Find(arr, nLeft, nRight); 20 int nMid = Partition(arr, nLeft, nRight, nMedian); 21 22 int k = nMid - nLeft + 1; 23 if (k == nMin) 24 return arr[nMid]; 25 else if (k > nMin) 26 return Select(arr, nLeft, nMid - 1, nMin); 27 else 28 return Select(arr, nMid + 1, nRight, nMin-k); 29 } 30 31 //找到数组中中位数的中位数 32 int Find(int arr[], int nLeft, int nRight) 33 { 34 int nLen = nRight - nLeft + 1; 35 36 int *pMedian = new int[nLen/5+1]; 37 38 int nStart, nEnd; 39 int j = 0; //表示有几个组 40 for (int i = 0; i < nLen; i ++) { 41 if (i%5 == 0) 42 nStart = nLeft + i; 43 if ((i+1)%5 == 0 || i == nLen - 1) { 44 nEnd = nLeft + i; 45 j ++; 46 int nRet = Insert(arr, nStart, nEnd); 47 pMedian[j-1] = nRet; 48 } 49 } 50 int nMedian = Select(pMedian, 0, j-1, (j-1)/2); 51 return nMedian; 52 } 53 54 //对每组5个元素的数组进行插入排序，找到每组的中位数 55 int Insert(int arr[], int nLeft, int nRight) 56 { 57 int nLen = nRight - nLeft + 1; 58 59 for (int j = 1; j < nLen; j ++) { 60 int key = arr[j]; 61 int i = j - 1; 62 while (i >= 0 && arr[i] > key) { 63 arr[i+1] = arr[i]; 64 i--; 65 } 66 arr[i+1] = key; 67 } 68 return arr[nLen/2]; 69 } 70 71 //略作修改过的Partition函数 72 int Partition(int arr[], int nLeft, int nRight, int nMedian) 73 { 74 //把中位数与看做主元，与最后一个元素交换 75 for (int i = nLeft; i <= nRight; i++) { 76 if (arr[i] == nMedian){ 77 Swap(arr[i], arr[nRight]); 78 break; 79 } 80 } 81 82 int nTemp = arr[nRight]; 83 int i = nLeft-1; 84 int j = nLeft; 85 86 while (j < nRight) { 87 if (arr[j] <= nTemp) { 88 Swap(arr[i+1], arr[j]); 89 i ++; 90 } 91 j ++; 92 } 93 Swap(arr[i+1], arr[nRight]); 94 return i + 1; 95 } 96 97 void Swap(int &m , int &n) 98 { 99 int t = m; 100 m = n; 101 n = t; 102 } 103 104 int main() 105 { 106 int arr[] = {7,4,6,9,2,1,5,8,3,0,12,23,78}; 107 cout << Select(arr, 0, 12, 11) << endl; 108 return 0; 109 }
我的公众号 「Linux云计算网络」(id: cloud_dev)，号内有 10T 书籍和视频资源，后台回复 「1024」 即可领取，分享的内容包括但不限于 Linux、网络、云计算虚拟化、容器Docker、OpenStack、Kubernetes、工具、SDN、OVS、DPDK、Go、Python、C/C++编程技术等内容，欢迎大家关注。
