链接：
http://codeforces.com/contest/718/problem/C
题意：
维护一个长度为n的数列a，支持下面两个操作：
1 l r x — increase all integers on the segment from l to r by values x;
2 l r — find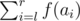 
, where f(x) is the x-th Fibonacci number. As this number may be large, you only have to find it modulo 109 + 7.
题解：
斐波那契可以有矩阵快速幂求得，所以我们的线段树的每个节点都是一个2*2的矩阵，
父亲节点就是儿子节点的和，儿子同时+x也就是父亲*（A^x）次方，因为矩阵满足分配律
这样就能用线段树来写了
代码：
31 struct Matrix { 32 int a[2][2]; 33 Matrix() { 34 memset(a, 0, sizeof(a)); 35 } 36 void init() { 37 rep(i, 0, 2) rep(j, 0, 2) 38 a[i][j] = (i == j); 39 } 40 Matrix operator+(const Matrix &B)const { 41 Matrix C; 42 rep(i, 0, 2) rep(j, 0, 2) 43 C.a[i][j] = (a[i][j] + B.a[i][j]) % MOD; 44 return C; 45 } 46 Matrix operator*(const Matrix &B)const { 47 Matrix C; 48 rep(i, 0, 2) rep(k, 0, 2) rep(j, 0, 2) 49 C.a[i][j] = (C.a[i][j] + 1LL * a[i][k] * B.a[k][j]) % MOD; 50 return C; 51 } 52 Matrix operator^(const int &n)const { 53 Matrix A = *this, res; 54 res.init(); 55 int p = n; 56 while (p) { 57 if (p & 1) res = res*A; 58 A = A*A; 59 p >>= 1; 60 } 61 return res; 62 } 63 }; 64 65 int n, m; 66 int a[MAXN]; 67 Matrix A, Tree[MAXN<<2], Lazy[MAXN<<2]; 68 69 void pushup(int rt) { 70 Tree[rt] = Tree[rt << 1] + Tree[rt << 1 | 1]; 71 } 72 73 void pushdown(int rt) { 74 Tree[rt << 1] = Lazy[rt] * Tree[rt << 1]; 75 Tree[rt << 1 | 1] = Lazy[rt] * Tree[rt << 1 | 1]; 76 Lazy[rt << 1] = Lazy[rt] * Lazy[rt << 1]; 77 Lazy[rt << 1 | 1] = Lazy[rt] * Lazy[rt << 1 | 1]; 78 Lazy[rt].init(); 79 } 80 81 void build(int l,int r,int rt){ 82 Lazy[rt].init(); 83 if (l == r) { 84 Tree[rt] = A^a[l]; 85 return; 86 } 87 int m = (l + r) >> 1; 88 build(lson); 89 build(rson); 90 pushup(rt); 91 } 92 93 void update(int L, int R, Matrix x, int l, int r, int rt) { 94 if (L <= l && r <= R) { 95 Tree[rt] = Tree[rt] * x; 96 Lazy[rt] = Lazy[rt] * x; 97 return; 98 } 99 pushdown(rt); 100 int m = (l + r) >> 1; 101 if (L <= m) update(L, R, x, lson); 102 if (R > m) update(L, R, x, rson); 103 pushup(rt); 104 } 105 106 int query(int L, int R, int l, int r, int rt) { 107 if (L <= l && r <= R) return Tree[rt].a[1][0]; 108 pushdown(rt); 109 int m = (l + r) >> 1; 110 int res = 0; 111 if (L <= m) res = (res + query(L, R, lson)) % MOD; 112 if (R > m) res = (res + query(L, R, rson)) % MOD; 113 return res; 114 } 115 116 int main() { 117 ios::sync_with_stdio(false), cin.tie(0); 118 A.a[0][0] = 1, A.a[0][1] = 1; 119 A.a[1][0] = 1, A.a[1][1] = 0; 120 cin >> n >> m; 121 rep(i, 1, n + 1) cin >> a[i]; 122 build(1, n, 1); 123 while (m--) { 124 int tp, l, r, x; 125 cin >> tp >> l >> r; 126 if (tp == 1) { 127 cin >> x; 128 update(l, r, A^x, 1, n, 1); 129 } 130 else cout << query(l, r, 1, n, 1) << endl; 131 } 132 return 0; 133 }