布拉休斯方程数值求解

布拉休斯方程如下：

[egin{equation} f f^{''}+2f^{'''}=0 \ f(0)=f^{'}(0)=0;f^{''}(0)=1 end{equation} ]

这是一个非线性常微分方程，下面我们利用四阶龙格库塔方法来求解该方程。

我们引入新的变量：

[egin{equation} y_1=f \ y_2=f^{'} \ y_3=f^{''} end{equation} ]

则布拉休斯方程可以等价的表示乘如下：

[egin{equation} left{ egin{aligned} &y_1^{'} = y_2 \ &y_2^{'} = y_3 \ &y_3^{'} = -frac{1}{2}y_1 y_3 end{aligned} ight . end{equation} ]

利用四阶龙哥库塔有：

[egin{equation} left{ egin{aligned} &y_{n+1}=y_n+frac{h}{6}(K_1+2K_2+2K_3+K_4) \ &K_1 = f(x_n, y_n) \ &K_2 = f(x_n+frac{h}{2}, y_n+frac{h}{2}K_1) \ &K_3 = f(x_n+frac{h}{2}, y_n+frac{h}{2}K_2) \ &K_4 = f(x_n+h, y_n+h K_3) \ end{aligned} ight . end{equation} ]

对于（3）式中的第一式利用龙哥库塔方法，有：

[egin{equation} left{ egin{aligned} &y_1^{n+1}=y_1^{n}+frac{h}{6}(K_{11}+2K_{12}+2K_{13}+K_{14}) \ &K_{11} = y_2^{n} \ &K_{12} = y_2^{n} + frac{h}{2}K_{11} \ &K_{13} = y_2^{n} + frac{h}{2}K_{12} \ &K_{14} = y_2^{n} + h K_{13} \ end{aligned} ight . end{equation} ]

同理，对于(3)中的第二式：

[egin{equation} left{ egin{aligned} &y_2^{n+1}=y_2^{n}+frac{h}{6}(K_{21}+2K_{22}+2K_{23}+K_{24}) \ &K_{21} = y_3^{n} \ &K_{22} = y_3^{n} + frac{h}{2}K_{21} \ &K_{23} = y_3^{n} + frac{h}{2}K_{22} \ &K_{24} = y_3^{n} + h K_{23} \ end{aligned} ight . end{equation} ]

对于(3)中的第三式：

[egin{equation} left{ egin{aligned} &y_3^{n+1}=y_3^{n}+frac{h}{6}(K_{31}+2K_{32}+2K_{33}+K_{34}) \ &K_{31} = -frac{1}{2}y_1^{n}y_3^{n} \ &K_{32} = -frac{1}{2}(y_1^{n} + frac{h}{2}K_{31})(y_3^{n} + frac{h}{2}K_{31}) \ &K_{33} = -frac{1}{2}(y_1^{n} + frac{h}{2}K_{32})(y_3^{n} + frac{h}{2}K_{32}) \ &K_{34} = -frac{1}{2}(y_1^{n} + hK_{33})(y_3^{n} + hK_{33}) \ end{aligned} ight . end{equation} ]

编写代码：

import numpy as np

# 四阶龙格库塔（RK4）
L = 10     # length of boundary
h = 0.1    # step length
N = int(L / h)
y1 = np.zeros(N)
y2 = np.zeros(N)
y3 = np.zeros(N)
y3[0] = 0.33206   # test value

for ii in range(N-1):
    k11 = y2[ii]
    k21 = y3[ii]
    k31 = -1 / 2 * y1[ii] * y3[ii]
    k12 = y2[ii] + h / 2 * k21
    k22 = y3[ii] + h / 2 * k31
    k32 = -1 / 2 * (y1[ii] + h / 2 * k11) * (y3[ii] + h / 2 * k31)
    k13 = y2[ii] + h / 2 * k22
    k23 = y3[ii] + h / 2 * k32
    k33 = -1 / 2 * (y1[ii] + h / 2 * k12) * (y3[ii] + h / 2 * k32)
    k14 = y2[ii] + h * k22
    k24 = y3[ii] + h * k32
    k34 = -1 / 2 * (y1[ii] + h * k13) * (y3[ii] + h * k33)
    y1[ii+1] = y1[ii] + h / 6 * (k11 + 2 * k12 + 2 * k13 + k14)
    y2[ii+1] = y2[ii] + h / 6 * (k21 + 2 * k22 + 2 * k23 + k24)
    y3[ii+1] = y3[ii] + h / 6 * (k31 + 2 * k32 + 2 * k33 + k34)

利用上面计算的结果，绘制图像如下：

import matplotlib.pyplot as plt
x = np.arange(N) * h
fig = plt.figure(figsize=(16, 9))
plt.plot(x, y2, '--', color='red')
# plt.xlabel('$eta=(u_e/
u x)^0.5$')
# plt.ylabel("$f^'=u/u_e$")
plt.xlabel('x')
plt.ylabel('f')
plt.grid()
plt.show()

图像如下：

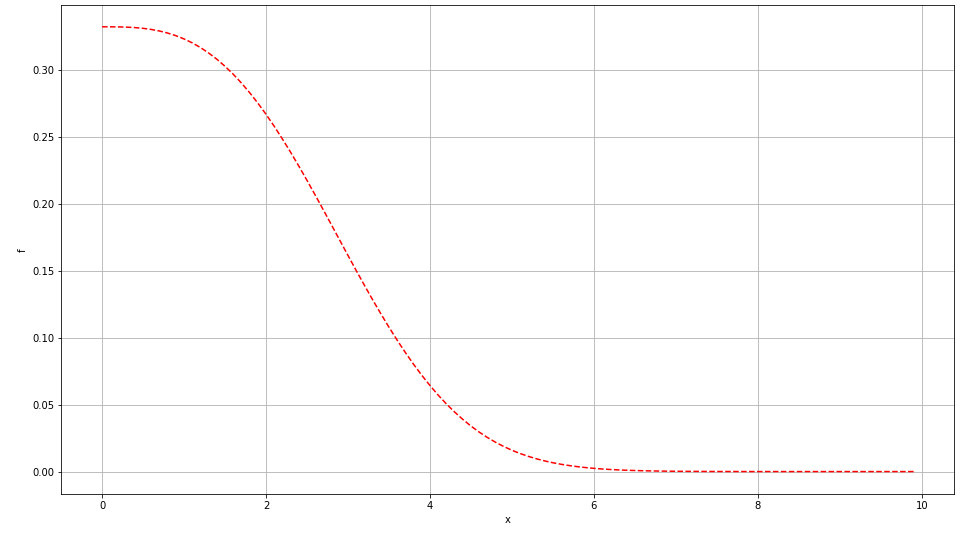
在上面计算中，我们给出一个尝试值y3[0]=0.33206。但是，其实我们并不知道(f^{''}(0))的值。因此采用打靶的思想进行确定。具体思路是给出一个(f^{''}(0))的值，计算(f)的值，根据插值来修正。（我们知道精确值为(f(infty)=1)）。具体代码如下：

# 采用修正算法来自动寻找初始值。

def RK4(ic):
    # 四阶龙格库塔（RK4）
    L = 40      # length of boundary
    h = 0.1     # step length
    N = int(L / h)
    y1 = np.zeros(N)
    y2 = np.zeros(N)
    y3 = np.zeros(N)
    y3[0] = ic

    for ii in range(N-1):
        k11 = y2[ii]
        k21 = y3[ii]
        k31 = -1 / 2 * y1[ii] * y3[ii]
        k12 = y2[ii] + h / 2 * k21
        k22 = y3[ii] + h / 2 * k31
        k32 = -1 / 2 * (y1[ii] + h / 2 * k11) * (y3[ii] + h / 2 * k31)
        k13 = y2[ii] + h / 2 * k22
        k23 = y3[ii] + h / 2 * k32
        k33 = -1 / 2 * (y1[ii] + h / 2 * k12) * (y3[ii] + h / 2 * k32)
        k14 = y2[ii] + h * k22
        k24 = y3[ii] + h * k32
        k34 = -1 / 2 * (y1[ii] + h * k13) * (y3[ii] + h * k33)
        y1[ii+1] = y1[ii] + h / 6 * (k11 + 2 * k12 + 2 * k13 + k14)
        y2[ii+1] = y2[ii] + h / 6 * (k21 + 2 * k22 + 2 * k23 + k24)
        y3[ii+1] = y3[ii] + h / 6 * (k31 + 2 * k32 + 2 * k33 + k34)
    return y2[-1]

epsilon = 1e-9
# 开始迭代测试修正
ic = 1
alpha = 0.3
for ii in range(20):
    print(ic)
    y3 = RK4(ic)
    error = y3 - 1.0
    if np.abs(error) < epsilon:
        break
    else:
        ic -= alpha * error

运行上面的程序，我们很容易得到(f^{''}(0))从初始值（尝试值1）降低到正确值0.33205。

1
0.6743617428806606
0.4932473770697171
0.4026815319928927
0.36152169076308643
0.34402498259791453
0.3368568758014264
0.3339705495653165
0.33281689350656146
0.33235717556926003
0.3321742068752738
0.3321014204467237
0.33207247103980964
0.3320609578581748
0.3320563792056564
0.33205455835342595
0.33205383423498663
0.33205354626735756
0.33205343174839597
0.3320533862065114