Kd树
实现k近邻法时,主要考虑的问题是如何对训练数据进行快速的k近邻搜索。k近邻法最简单有效的方法是线性扫描(穷举搜索),即要计算输入实例与每一个训练实例的距离,再查找k近邻,当训练数据很大时,计算非常耗时,为提高KNN搜索效率,就引入了kd树的概念。
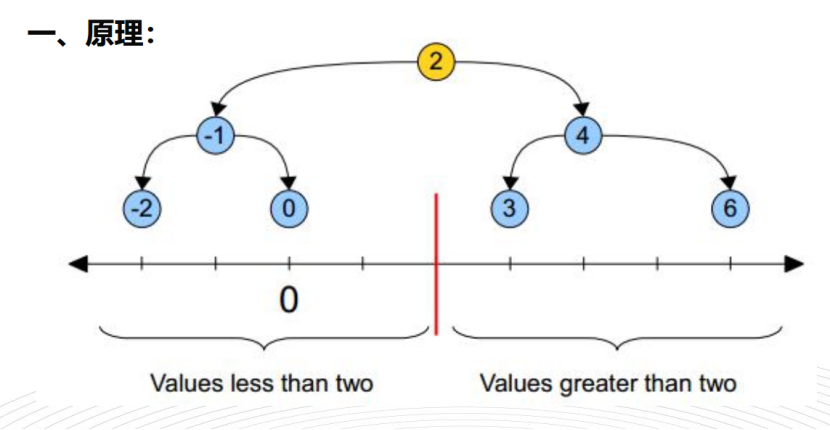
Kd树原理其实跟二分查找是一样的,比如上面这些数,我要查找0这个数,我先把上面这些数进行排序,找到中间的那个树为2,因0比2小,所以接下来查找的是-2--0这个区间的数据,另半边就无需查找,在-2--0之间再进行二分取中间的树为-1,0比-1大,这样就确定了0这个数。
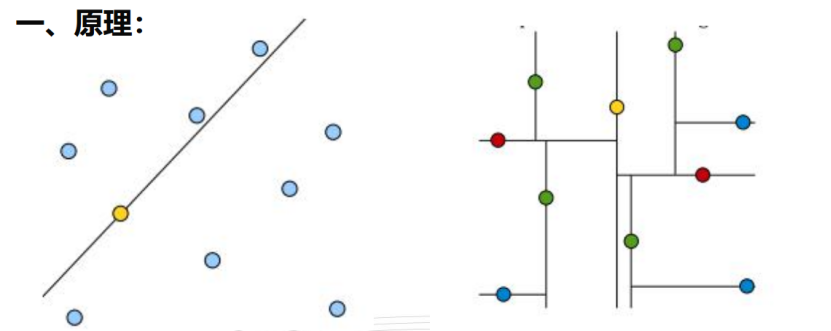
上图中,黄色的点作为根节点,上面的点作为左子树,下面的点作为右子树,接下来不断地划分,分割的那条线叫作分割超平面,在一维中是点,二维中是线,三维中是面
kd树是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形结构。Kd树是一种二叉树,表示对k维空间的一个划分,构造kd树相当于不断地用垂直于坐标轴的超平面对k维空间进行切分,构成一系列的k维超矩形区域。kd树的每个结点对应于一个k维超矩形区域。Kd树的每个结点对应于一个k维超矩形区域。利用kd树可以省去对大部分数据的搜索,从而减少搜索时间
kd树的构造方法:
(1)、构造根结点,使根结点对应于k维空间中包含所有实例点的矩形区域。
(2)、对过递归方法,不断对k维空间进行切分,生成子结点。在超矩形区域上选择一个坐标轴和在此坐标轴上 的一个切分点,确定一个超平面,这个超平面通过选定的切分点并垂直于选定的坐标轴,将当前超矩形区域切分为左右两个子区域(子结点);这时,实例被分到两个区域
(3)、上述过程直到子区域没有实例终止(终止时的结点为叶结点),在此过程中,将实例保存在相应的结点上。
(4)、通常,循环的选择坐标对空间切分,选择训练实例点在坐标轴上的中位数为切分点,这样得到的kd树是平衡的(平衡二叉树:它是一颗空树,或其左子树和右子树的深度之差的绝对值不超过1,且它的左子树和右子树是平衡二叉树)
KD树中每个节点都是一个向量,和二叉树划分不同的是,kd树每层需要选定向量中 的某一维,然后根据这一维左小右大的方式划分数据。在构建二叉树时,有两个问题需要解决:
(1)、选择向量的哪一维进行划分
(2)、如何划分 数据
解决上述问题的关键是每次选择中位数来进行划分