1、卡方检验理论
1.1、 简介
总体的分布函数完全未知或只知形式、但不知其参数的情况,为了推断总体的某些未知特性,提出某些关于总体的假设。我们要根据样本对所提出的假设作出是接受,还是拒绝的决策。假设检验是作出这一决策的过程。卡方检验即是假设检验的一种。
1.2、卡方检验基本思想
首先假设H0成立,基于此前提计算出χ2值,它表示观察值与理论值之间的偏离程度。根据χ2分布及自由度可以确定在H0假设成立的情况下获得当前统计量及更极端情况的概率P。如果P值很小,说明观察值与理论值偏离程度太大,应当拒绝无效假设,表示比较资料之间有显著差异;否则就不能拒绝无效假设,尚不能认为样本所代表的实际情况和理论假设有差别
1.3、数学公式
Pearson χ2 计算公式:
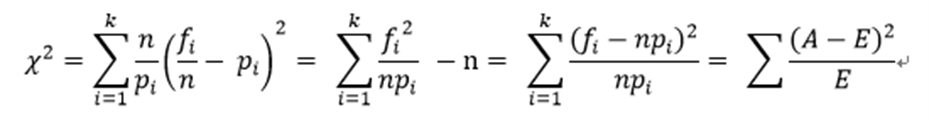
其中:k为分类数,i水平的观察频数,n为总频数,i水平的期望概率
由卡方的计算公式可知,当观察频数与期望频数完全一致时,χ2值为0;观察频数与期望频数越接近,两者之间的差异越小,χ2值越小;反之,观察频数与期望频数差别越大,两者之间的差异越大,χ2值越大。换言之,大的χ2值表明观察频数远离期望频数,即表明远离假设。小的χ2值表明观察频数接近期望频数,接近假设。因此,χ2是观察频数与期望频数之间距离的一种度量指标,也是假设成立与否的度量指标。如果χ2值“小”,研究者就倾向于不拒绝H0;如果χ2值大,就倾向于拒绝H0。至于χ2在每个具体研究中究竟要大到什么程度才能拒绝H0,则要借助于卡方分布求出所对应的P值(p-value)来确定。
1.4、卡方检验作用
卡方检验主要有以下两种作用:
1) 皮尔森独立性检验(Pearson's independence test)
验证从两个变量抽出的配对观察值组是否互相独立。例如:例如:每次都从A国和B国各抽一个人,看他们的反应是否与国籍无关。
2)适度检验(Goodness of Fit test)
实际执行多项式试验而得到的观察次数,与虚无假设的期望次数相比较,称为卡方适度检验,即在于检验二者接近的程度,利用样本数据以检验总体分布是否为某一特定分布的统计方法。
2、MLlib与卡方检验
2.1、MLlib库简介
MLlib 是Spark对常用的机器学习算法的实现库,同时包括相关的测试和数据生成器。
2.2、MLlib卡方检验
卡方检验是在spark mllib 1.1版本新增加的功能,其源码文件在stat包中。
2.2.1、实现
MLlib中卡方检验依照皮尔森卡方(pearson)检验实现,可以用其进行独立性检验及适度检验。其对外提供接口有如下三种:
(1) def chiSquaredMatrix(counts:Matrix,methodName:String=PEARSON.name)
:ChiSqTestResult
(2) def chiSquaredFeatures(data: RDD[LabeledPoint],methodName: String = PEARSON.name)
:Array[ChiSqTestResult]
(3) def chiSquared(observed: Vector, expected: Vector = Vectors.dense(Array[Double]()),
methodName: String = PEARSON.name):ChiSqTestResult
其中(1)、(2)用于独立性检验,(3)用于适度检验。
方法(1) 中参数是统计后的对象的不同特征在特定取值区间出现的频数。因此可直接对传入进行卡方数学计算。由于统计后数据较小,程序采用串行方式处理。
方法(2) 中参数为RDD[LabeledPoint]类型的数据。LabeledPoint格式的数据多用于机器学习方面,如回归分析等,其数据格式为label:features。此种类型的数据多为收集的原始数据或经过维归约、聚集等手段处理过的数据,需要进行频数统计才可进行卡方数学计算。通过分析源码本方法先将RDD[LabeledPoint]类型的数据转换成矩阵,然后调用方法(1)。
方法(3) 与方法(1)相似,直接利用参数提供数据,根据卡方定义进行数学计算。
2.2.2、具体流程
通过2.2.1分析可知,上述方法(2)过程最为复杂,其包含数据预处理阶段(频数统计并转换成矩阵)及处理阶段(卡方数学计算)两个过程,下面以方法(2)程序逻辑为基础就这两个过程分别进行讨论。
2.2.2.1、预处理阶段
预处理阶段要做的主要任务为:将RDD[LabeledPoint]类型的数据转换为三元组,然后分别对转换后的三元组进行频数统计,最后根据统计信息分别将每个特征所对应三元组转换成矩阵并进行卡方计算。
下面通过举例,详细说明预处理过程,假如采集到如下数据:
|
姓名 |
性别 |
年龄 |
文化程度 |
结婚次数 |
…… |
|
张三 |
男 |
22 |
大学 |
1 |
|
|
李四 |
女 |
20 |
未读大学 |
1 |
|
|
王五 |
男 |
29 |
未读大学 |
3 |
|
|
赵六 |
男 |
27 |
大学 |
2 |
|
|
孙七 |
女 |
21 |
未读大学 |
2 |
|
|
钱八 |
男 |
23 |
大学 |
1 |
|
|
蒋九 |
女 |
37 |
未读大学 |
3 |
|
|
…… |
…… |
…… |
…… |
…… |
|
|
|
|
|
|
|
现在要用这批数据检验结婚次数是否与文化程度有关, 通过降维、聚集等手段进行转换,结果如下图所示:
|
文化程度 |
结婚次数 |
|
大学 |
1次 |
|
未读大学 |
1次 |
|
未读大学 |
超过1次 |
|
大学 |
超过1次 |
|
未读大学 |
超过1次 |
|
大学 |
1次 |
|
未读大学 |
超过1次 |
然后用上述处理过的数据创建RDD[LabeledPoint],其中label为“大学|未读大学”,features为“{1次,超过1次}”,然后交由2.2.1中所述MLlib卡方提供的接口(2)处理。处理过程如下:
1> 将RDD[LabeledPoint] 映射成RDD[(col,feature,label),1],其中col为feature在features中所在的列的下标,feature为特征,label为某对象,1为初始频数。对应上表来说数据样例为:(0,一次,大学): 1 ;(0,一次以上,大学): 1
2> 将RDD[(col,feature,label),1] 按(col,feature,label)进行合并,生成Map[(col, feature,
label), n],其中n代表(col, feature,label)一共出现n次。对应上表数据样例为:(0,一次,大学): 2 ;(0,一次以上,大学): 1
3> 将Map[(col,feature,label),n]以三元组(col,feature,label)中col进行分组。然后统计每个组中无重复feature值的个数及根据唯一label个数创建矩阵,矩阵单元格的值为(col,feature,label)的个数n。因样例数据feature为1维所以2>中结果即为最终结果。
4> 对矩阵进行数学计算得出结论(此部分将在下文处理阶段详细说明)。
其中1>,2>步为并行处理部分,3>,4>步串行处理部分。上述程序流程图为:
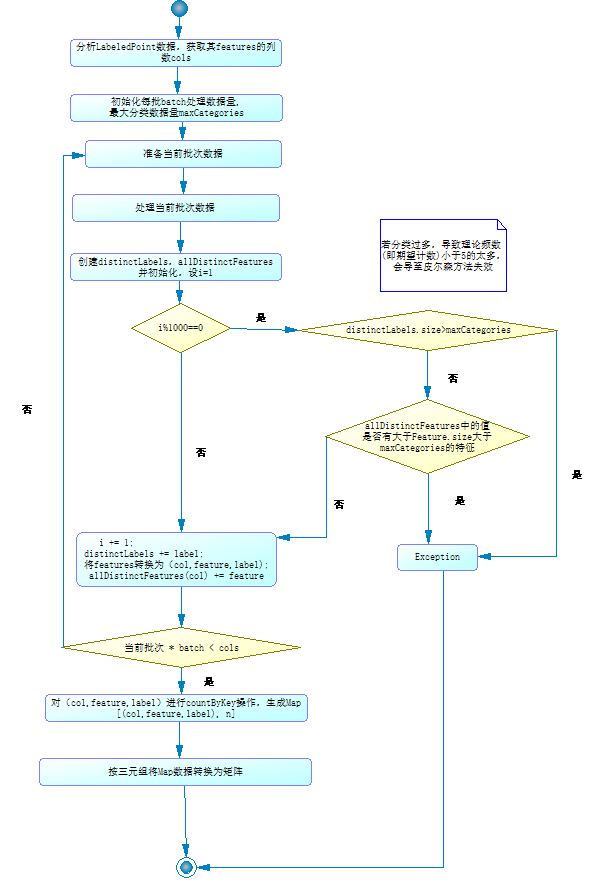
其中countByKey操作中RDD转换过程如下图:
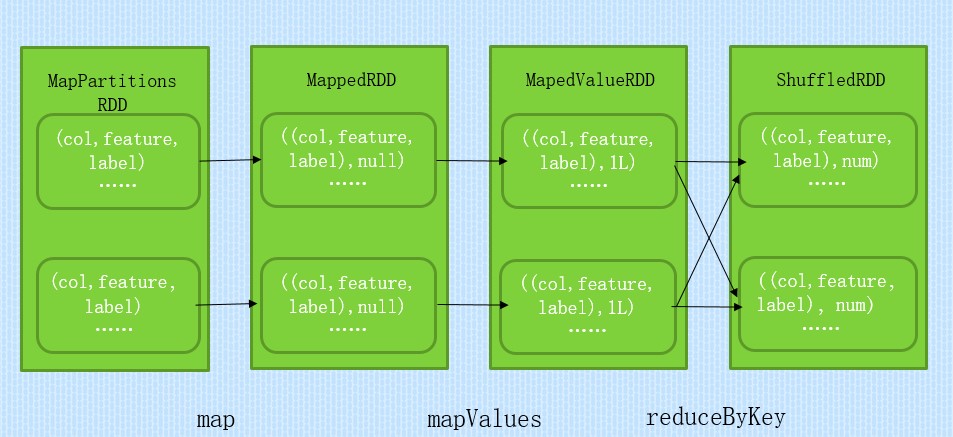
三元组转换为矩阵的具体流程为:
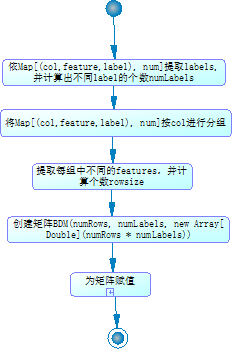
2.2.2.2、处理阶段
利用预处理阶段产生的矩阵,计算数学期望,自由度,p值,通过p值决定接受还是拒绝原假设。此阶段为翻译卡方检验数学公式不再详述。
2.2.3、不足
1)本程序仅根据皮尔森卡方进行实现,当某特征出现理论(期望)频数小于5时,会使“近似于卡方分配”的假设不可信,本程序的处理方法是直接抛出异常。可否通过修正(叶氏连续修正),使存在期望频数小于5时仍得出可信的结果。
2)本程序预处理阶段将RDD[LabeledPoint]转换成Map[(col,feature,label),num]过程是并行的,从Map[(col,feature,label),num]转换成矩阵过程及计算卡方的过程为串行处理。由源码分析知RDD 做为参数的卡方检验接口是检测每一个feature与label的独立性。不同feature这间无影响,可以进行并行处理。
附源码:
/*
* Licensed to the Apache Software Foundation (ASF) under one or more
* contributor license agreements. See the NOTICE file distributed with
* this work for additional information regarding copyright ownership.
* The ASF licenses this file to You under the Apache License, Version 2.0
* (the "License"); you may not use this file except in compliance with
* the License. You may obtain a copy of the License at
*
* http://www.apache.org/licenses/LICENSE-2.0
*
* Unless required by applicable law or agreed to in writing, software
* distributed under the License is distributed on an "AS IS" BASIS,
* WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
* See the License for the specific language governing permissions and
* limitations under the License.
*/
package org.apache.spark.mllib.stat.test
import breeze.linalg.{DenseMatrix => BDM}
import org.apache.commons.math3.distribution.ChiSquaredDistribution
import org.apache.spark.{SparkException, Logging}
import org.apache.spark.mllib.linalg.{Matrices, Matrix, Vector, Vectors}
import org.apache.spark.mllib.regression.LabeledPoint
import org.apache.spark.rdd.RDD
import scala.collection.mutable
/**
* Conduct the chi-squared test for the input RDDs using the specified method.
* Goodness-of-fit test is conducted on two `Vectors`, whereas test of independence is conducted
* on an input of type `Matrix` in which independence between columns is assessed.
* We also provide a method for computing the chi-squared statistic between each feature and the
* label for an input `RDD[LabeledPoint]`, return an `Array[ChiSquaredTestResult]` of size =
* number of features in the input RDD.
*
* Supported methods for goodness of fit: `pearson` (default)
* Supported methods for independence: `pearson` (default)
*
* More information on Chi-squared test: http://en.wikipedia.org/wiki/Chi-squared_test
*/
/**
* 卡方检验
*/
private[stat] object ChiSqTest extends Logging {
/**
* @param name String name for the method.
* @param chiSqFunc Function for computing the statistic given the observed and expected counts.
*/
/**
* case 样例类,进行模式匹配
* @param name method名称
* @param chiSqFunc 用给定的观察值及期望值 计算分析
*/
case class Method(name: String, chiSqFunc: (Double, Double) => Double)
// Pearson's chi-squared test: http://en.wikipedia.org/wiki/Pearson%27s_chi-squared_test
/**
* 样例类Method 实例
* 皮尔森卡方计算公式
* 根据(observed-expected)^2 /expected计算 卡方值
*/
val PEARSON = new Method("pearson", (observed: Double, expected: Double) => {
val dev = observed - expected
dev * dev / expected
})
// Null hypothesis for the two different types of chi-squared tests to be included in the result.
//零假设:又称原假设,指进行统计检验时预先建立的假设, 零假设成立时,有关统计量应服从已知的某种概率分布.
object NullHypothesis extends Enumeration {
type NullHypothesis = Value
val goodnessOfFit = Value("observed follows the same distribution as expected.")
val independence = Value("the occurrence of the outcomes is independent.")
}
// Method identification based on input methodName string
/**
* 根据 methodName 获取卡方检验Method实例 , 本方法现在: 只提供皮尔森方法
* @param methodName 卡方检验方法名
*/
private def methodFromString(methodName: String): Method = {
methodName match { //…… 模式匹配
case PEARSON.name => PEARSON
case _ => throw new IllegalArgumentException("Unrecognized method for Chi squared test.")
}
}
/**
* Conduct Pearson's independence test for each feature against the label across the input RDD.
* The contingency table is constructed from the raw (feature, label) pairs and used to conduct
* the independence test.
* Returns an array containing the ChiSquaredTestResult for every feature against the label.
*/
/**
* 皮尔森独立性检验:验证从两个变量抽出的配对观察值组是否互相独立
* (例如:每次都从A国和B国各抽一个人,看他们的反应是否与国籍无关)
* @param data 待检测的数据 RDD[LabeledPoint] 类型
* @param methodName 使用的检验方法
* @result Array[ChiSqTestResult] 返回值
*/
def chiSquaredFeatures(data: RDD[LabeledPoint],
methodName: String = PEARSON.name): Array[ChiSqTestResult] = {
val maxCategories = 10000 //最大分类
val numCols = data.first().features.size //特征值中有多少种数据
val results = new Array[ChiSqTestResult](numCols) //存储卡方检验结果:numCols个元素的卡方检验结果数组
var labels: Map[Double, Int] = null
// at most 1000 columns at a time
val batchSize = 1000 //每批数据量
var batch = 0 //批次
while (batch * batchSize < numCols) { //处理
// The following block of code can be cleaned up and made public as
// chiSquared(data: RDD[(V1, V2)])
val startCol = batch * batchSize //开始执行位置
val endCol = startCol + math.min(batchSize, numCols - startCol) //相对startCol的偏移量
val pairCounts = data.mapPartitions { iter => //对每个分区执行iter指向操作
val distinctLabels = mutable.HashSet.empty[Double] //不同的标签(研究对象分类)
/*创建一个Map对象,并初始化:key为列的编号,value用空的HashSet*/
val allDistinctFeatures: Map[Int, mutable.HashSet[Double]] =
Map((startCol until endCol).map(col => (col, mutable.HashSet.empty[Double])): _*)
var i = 1 //计数器,避免频繁进行判断
/*对此分片进行flatMap操作, 将LabeledPoint(label, features) 转换成三元组*/
iter.flatMap { case LabeledPoint(label, features) =>
if (i % 1000 == 0) {
/*若分类过多,导致理论频数(即期望计数)小于5的太多,会导至皮尔森方法失效*/
if (distinctLabels.size > maxCategories) {
throw new SparkException(s"Chi-square test expect factors (categorical values) but "
+ s"found more than $maxCategories distinct label values.")
}
allDistinctFeatures.foreach { case (col, distinctFeatures) =>
if (distinctFeatures.size > maxCategories) {
throw new SparkException(s"Chi-square test expect factors (categorical values) but "
+ s"found more than $maxCategories distinct values in column $col.")
}
}
}
i += 1
distinctLabels += label
/*将features,加上索引,然后切片,再转将其通过map 操作 赋值到allDistinctFeatures*/
features.toArray.view.zipWithIndex.slice(startCol, endCol).map { case (feature, col) =>
allDistinctFeatures(col) += feature
(col, feature, label)
}
}
}.countByValue()
if (labels == null) {
// Do this only once for the first column since labels are invariant across features.
/*
*取出col 是startCol(实质每行一个分类,此filter即相当于从原数据每一行中拿出第一个)的数据,
*将label取出加入labels
* 方法仅执行一次。
*/
labels =
pairCounts.keys.filter(_._1 == startCol).map(_._3).toArray.distinct.zipWithIndex.toMap
}
/*标签,标识矩阵的列, (因为矩阵是列优先存储的)*/
val numLabels = labels.size
pairCounts.keys.groupBy(_._1).map { case (col, keys) =>
val features = keys.map(_._2).toArray.distinct.zipWithIndex.toMap
val numRows = features.size //特征值个数, 矩阵的行
val contingency = new BDM(numRows, numLabels, new Array[Double](numRows * numLabels)) //创建(空)矩阵
/*赋值操作*/
keys.foreach { case (_, feature, label) =>
val i = features(feature)
val j = labels(label)
contingency(i, j) += pairCounts((col, feature, label))
}
/*转换为Spark mllib库中的矩阵,并对矩阵作卡方检验*/
results(col) = chiSquaredMatrix(Matrices.fromBreeze(contingency), methodName)
}
batch += 1
}
results
}
/*
* Pearson's goodness of fit test on the input observed and expected counts/relative frequencies.
* Uniform distribution is assumed when `expected` is not passed in.
*/
/**
* 适度检验(Goodness of Fit test):实际执行多项式试验而得到的观察次数,与虚无假设的期望次数相比较,
* 称为卡方适度检验,即在于检验二者接近的程度,利用样本数据以检验总体分布是否为某一特定分布的统计方法
* @param observed 观察值
* @param expected 期望值(理论值), 若为均匀分布, 此参数可为空。
* @param methodName 检验方法名(默认皮尔森, 现阶段只实现了皮尔森)
*/
def chiSquared(observed: Vector,
expected: Vector = Vectors.dense(Array[Double]()),
methodName: String = PEARSON.name): ChiSqTestResult = {
// Validate input arguments
val method = methodFromString(methodName) //获取检验方法
/*期望值存在条件下,判断观察值与期望值的个数是否相等(也就是是否配对)*/
if (expected.size != 0 && observed.size != expected.size) {
throw new IllegalArgumentException("observed and expected must be of the same size.")
}
val size = observed.size
/*若分类过多,导致理论频数(即期望计数)小于5的太多,会导至皮尔森方法失效*/
if (size > 1000) {
logWarning("Chi-squared approximation may not be accurate due to low expected frequencies "
+ s" as a result of a large number of categories: $size.")
}
val obsArr = observed.toArray
/*若传入的期望值不存在元素 则Array初始化为 1.0/size,否则传入参数值 */
val expArr = if (expected.size == 0) Array.tabulate(size)(_ => 1.0 / size) else expected.toArray
if (!obsArr.forall(_ >= 0.0)) { //判断是否存在< 0.0元素
throw new IllegalArgumentException("Negative entries disallowed in the observed vector.")
}
if (expected.size != 0 && ! expArr.forall(_ >= 0.0)) {
throw new IllegalArgumentException("Negative entries disallowed in the expected vector.")
}
// Determine the scaling factor for expected
val obsSum = obsArr.sum //观察值的频次和
val expSum = if (expected.size == 0.0) 1.0 else expArr.sum //期望值之和
val scale = if (math.abs(obsSum - expSum) < 1e-7) 1.0 else obsSum / expSum //???????????
// compute chi-squared statistic
/*
* zip拉链操作, 组成(obs, exp)对,
* 然后对通过foldLeft(0.0) 求每一对的卡方值,并累加… 其中参数 0.0 为累加和的初始值
*/
val statistic = obsArr.zip(expArr).foldLeft(0.0) { case (stat, (obs, exp)) =>
if (exp == 0.0) {
if (obs == 0.0) {
throw new IllegalArgumentException("Chi-squared statistic undefined for input vectors due"
+ " to 0.0 values in both observed and expected.")
} else {
return new ChiSqTestResult(0.0, size - 1, Double.PositiveInfinity, PEARSON.name,
NullHypothesis.goodnessOfFit.toString)
}
}
if (scale == 1.0) {
stat + method.chiSqFunc(obs, exp)
} else {
stat + method.chiSqFunc(obs, exp * scale)
}
}
val df = size - 1
val pValue = 1.0 - new ChiSquaredDistribution(df).cumulativeProbability(statistic)
new ChiSqTestResult(pValue, df, statistic, PEARSON.name, NullHypothesis.goodnessOfFit.toString)
}
/*
* Pearson's independence test on the input contingency matrix.
* TODO: optimize for SparseMatrix when it becomes supported.
*/
/**
* 独立性检验
* @param counts 要检测的数据(矩阵)
* @param methodName 使用的检测方法(默认:皮尔森)
*/
def chiSquaredMatrix(counts: Matrix, methodName:String = PEARSON.name): ChiSqTestResult = {
val method = methodFromString(methodName) //获取Method (case类)
val numRows = counts.numRows //矩阵行数
val numCols = counts.numCols //矩阵列数
// get row and column sums
val colSums = new Array[Double](numCols) //存放每列数据和(用于计算概率)
val rowSums = new Array[Double](numRows) //存放每行数据和
val colMajorArr = counts.toArray //存在所有数据(用于计算 样本总数)
var i = 0
while (i < colMajorArr.size) {
val elem = colMajorArr(i)
if (elem < 0.0) {
throw new IllegalArgumentException("Contingency table cannot contain negative entries.")
}
colSums(i / numRows) += elem //赋值
rowSums(i % numRows) += elem //赋值
i += 1
}
val total = colSums.sum //计算样本总量
// second pass to collect statistic
var statistic = 0.0
var j = 0
while (j < colMajorArr.size) {
val col = j / numRows
val colSum = colSums(col)
if (colSum == 0.0) {
throw new IllegalArgumentException("Chi-squared statistic undefined for input matrix due to"
+ s"0 sum in column [$col].")
}
val row = j % numRows
val rowSum = rowSums(row)
if (rowSum == 0.0) {
throw new IllegalArgumentException("Chi-squared statistic undefined for input matrix due to"
+ s"0 sum in row [$row].")
}
val expected = colSum * rowSum / total //计算期望值
statistic += method.chiSqFunc(colMajorArr(j), expected) //计算卡方值、并叠加至statistic中
j += 1
}
val df = (numCols - 1) * (numRows - 1) //计算自由度
if (df == 0) {
// 1 column or 1 row. Constant distribution is independent of anything.
// pValue = 1.0 and statistic = 0.0 in this case.
new ChiSqTestResult(1.0, 0, 0.0, methodName, NullHypothesis.independence.toString)
} else {
/*
* cumulativeProbability() 依据下面理论进行实现
* <a href="http://mathworld.wolfram.com/Chi-SquaredDistribution.html">
* 自由度为n的卡方分布是 a=n/2 和 λ = 1/2 的伽马分布
* 此方法计算的概率是 P{X <= x} ;
*
* 当x是某个常数,选择x是为了得到想要的检验显著性水平a, 也就是说x的选择满足Ho为真时, 应为:P(X > x) = a;
* 与上述方法计算值互补
* 又pValue = P{X > x} = a;
* pValue 为拒绝原假设的最小显著性水平
*/
val pValue = 1.0 - new ChiSquaredDistribution(df).cumulativeProbability(statistic)
//生成结果(根据pValue值进行比较,得出独立性强弱)
new ChiSqTestResult(pValue, df, statistic, methodName, NullHypothesis.independence.toString)
}
}
}
以上皆个人理解,请各位批评指正
http://www.cnblogs.com/barrenlake/p/4354579.html