Mr. Kitayuta vs. Bamboos
题目链接:http://codeforces.com/problemset/problem/505/E
参考:http://blog.csdn.net/qpswwww/article/details/46316647
贪心,二分
从数据规模上看,算法复杂度只能为O(n)或者O(nlgn),似乎不能直接求值,考虑二分MAX将求值问题转化为判定性问题。然而考虑到砍伐后竹子高度变为0的特殊情况,考虑倒着做,即初始时每个竹子高度均为MAXi,每天晚上每个竹子会减少高度a[i],每天白天可以选择对其中不超过K个竹子选择将其的高度增加P,并且保证任何时刻任何竹子高度均大于等于0,m天后是否可以让每个竹子高度均大于等于h[i]。
证明倒着推的正确性:只有在m天后每个竹子高度均大于等于h[i],才能让所有的竹子按照原来正向的顺序,以和倒着做相同的操作反过来让每个竹子最终的高度小于等于MAXi,见下图,绿色线代表倒着推的话一根竹子的每天生长情况,蓝色线代表正着推的话一根竹子的每天生长情况(来自Codeforces官方题解)
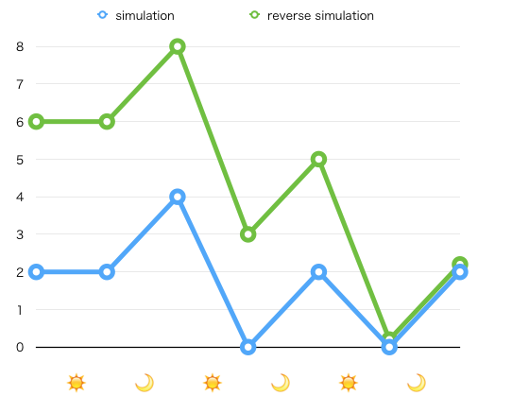
可以发现如果每天对这个竹子的操作相同的话,要想让最后的这个竹子的高度和倒着推的高度一样,之前每天正着推的高度都必须小于等于倒着推的高度。
首先计算从MAXi开始,最多经历多少天自由生长(减少高度a[i]),竹子的高度变为负数,然后用一个小顶堆维护竹子变为负数的天数(时间越小,越快变为负数),每天取k个竹子进行砍伐(拔高处理)。若存在某一天来不及拔高竹子(存在某个竹子的高度在这一天之前就变为0了),就可以立刻判定m天后不能可以让每个竹子高度均大于等于h[i]。
现在我们让所有竹子倒过来生长,最终每个竹子高度均大于等于0后,就需要让每个竹子的高度拔高,使得它们最终高度大于等于h[i],显然此时由于在生长过程中,每个竹子在任意时刻高度均大于等于0,故此时补充的操作无论是在何时发生都是一样的。这时直接通过数学方法,计算每个竹子和h[i]之间相差的高度以考虑需要补上多少次操作就够了。
这道题是看着题解跪着做完的Orz,感觉对二分的理解更深了一些,二分处理的都是判定性问题,不能直接求值。
代码如下:
1 #include<cstdio> 2 #include<queue> 3 #include<iostream> 4 #define N 100000 5 #define LL long long 6 #define mid ((l+r)>>1) 7 using namespace std; 8 const LL MAX=1e15; 9 LL n,m,k,p,l,r; 10 LL h[N+5],a[N+5]; 11 LL now[N+5]; 12 typedef pair<LL,LL> P; 13 struct cmp{ 14 bool operator()(P a,P b){ 15 return a.first>b.first;//小顶堆 16 } 17 }; 18 bool judge(LL x){ 19 priority_queue<P,vector<P>,cmp> q; 20 for(LL i=0;i<n;++i){ 21 now[i]=x;//刚开始竹子的高度为MAXi 22 if(x-m*a[i]>=0)continue;//不需要补充高度 23 q.push(make_pair(x/a[i],i));//P(到零的天数,下标) 24 } 25 LL times=0;//砍伐次数 26 for(;times<=k*m;times++){ 27 if(q.empty())break; 28 P temp=q.top(); 29 q.pop(); 30 if(temp.first<=times/k)return 0;//来不及补充高度,竹子在k天前就长成负数 31 LL index=temp.second; 32 now[index]+=p; 33 if(now[index]-m*a[index]>=0)continue;//不需要补充高度 34 q.push(make_pair(now[index]/a[index],index)); 35 } 36 if(times>k*m)return 0; 37 for(int i=0;i<n;++i){ 38 LL temp=m*a[i]+h[i]-now[i]; 39 if(temp<=0)continue; 40 else times+=((temp/p)+(LL)(temp%p!=0));//到h[i]还需要多少次补充高度 41 if(times>k*m)return 0; 42 } 43 return 1; 44 } 45 int main(void){ 46 scanf("%I64d%I64d%I64d%I64d",&n,&m,&k,&p); 47 l=1,r=MAX; 48 for(LL i=0;i<n;++i) 49 scanf("%I64d%I64d",&h[i],&a[i]); 50 while(l<r){//二分 51 if(judge(mid))r=mid; 52 else l=mid+1; 53 } 54 printf("%I64d ",l); 55 }