There are two sorted arrays nums1 and nums2 of size m and n respectively. Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).
题意:
两个排序后的数组nums1 和nums2,长度分别是m,n,找出其中位数,并且时间复杂度:O(log(m+n))
最愚蠢的方法:
两个数组合并成一个,排序,取出中位数
Java程序:
public class Solution { public double findMedianSortedArrays(int[] nums1, int[] nums2) { int m = nums1.length; int n = nums2.length; int median_index = (m+n)/2; int nums[] = new int[m+n]; if(m!=0) for(int k=0;k<m;k++) nums[k] = nums1[k]; if(n!=0) for(int k=0;k<n;k++) nums[m+k] = nums2[k]; Arrays.sort(nums); if((m+n)%2==1) return nums[median_index]; else return (nums[median_index]+nums[median_index-1])/2.0; } }
无耻的又用Python实现了一遍
class Solution(object): def findMedianSortedArrays(self, nums1, nums2): """ :type nums1: List[int] :type nums2: List[int] :rtype: float """ m = len(nums1) n = len(nums2) median_index = (m+n)/2 nums=[num for num in nums1] for num in nums2: nums.append(num) nums.sort() if((m+n)%2==1): return nums[median_index] else: return (nums[median_index]+nums[median_index-1])/2.0
说明一下:
Python中 sorted(list)排序是直接返回排序后的结果,原list没有改变,而list.sort() 不返回排序后的结果,结果更新list
正确方法:
问题转化为:nums1和nums2合并排序后的第k个元素
主要思想是:每次剔除部分对求第k个元素没有用的数据
假设nums1和nums2原始序列是升序的,则是求合并后升序的第k个元素,或者第k大元素
假设nums1和nums2原始序列是降序的,则是求合并后降序的第k个元素,或者第k小元素
下面假设是升序
m = nums1.length
n = nums2.length
若 nums1是空的,结果就是 nums2[k]
若 nums2是空的,结果就是 nums1[k]
若 k==0,返回nums1[0] 、nums2[0]中的较小者
对于其他情况:
为了好说明,定义变量:nums1Start,nums1End,nums2Start,nums2End
我们要求的是合并后的第k大的数
小于第k大的数是没有用的
对于合并排序后的前k个数,理想情况下,是均匀的分布在nums1 和nums2中
k个数中nums1中占:nums1Mid = nums1Len*k/(nums1Len+nums2Len)个 这里除法取的是下界
k个数中nums2中占:nums2Mid = k – nums1Mid – 1 个 这里是因为下标是从0开始
由于我们定义了开始位置,则:
nums1Mid = nums1Mid + nums1Start
nums2Mid = nums2Mid + nums2Start
下面比较这两个位置对应元素的大小:nums1[nums1Mid ] nums2[nums2Mid]
若:nums1[nums1Mid ] > nums2[nums2Mid] 说明:第k大的数在nums1中的nums1Start 到nums1Mid 之间 和 nums2 中nums2Mid 到nums2End之间
可以发现我们去除的有效部分只是nums2中的nums2Start 到 nums2Mid之间的元素,而nums1中 nums1Mid到nums1End之间的原始已经是大于 第k个元素了。
所以更新k,k = k - (nums2Mid – nums2Start + 1)
同时更新:nums1End = nums1Mid ,nums2Start = nums2Mid + 1,其他不变
若:nums1[nums1Mid ] < nums2[nums2Mid] 说明:第k大的数在num1中的num1Mid到nums1End之间 和 nums2中的nums2Start到nums2Mid之间
更新k,k = k - (nums1Mid – nums1Start + 1)
同时更新: nums1Start = nums1Mid + 1,nums2End = nums2Mid ,其他不变
若:nums1[nums1Mid ] = nums2[nums2Mid]
这里正好是第k个数,就是所求答案
对于上面两种情况,继续递归求解
关于时间复杂度:在最坏的情况下,每次都要去除k/2的元素,则log(k) = log((m+n)/2) = log(m+n)
Java程序:
public class Solution { public double findMedianSortedArrays(int[] nums1, int[] nums2) { int m = nums1.length; int n = nums2.length; if((m+n)%2==1)//odd return (double)findKth(nums1,0,m-1,nums2,0,n-1,((m+n)/2)); else return (findKth(nums1,0,m-1,nums2,0,n-1,(m+n)/2)+findKth(nums1,0,m-1,nums2,0,n-1,(m+n)/2-1))/2.0; } public int findKth(int[] nums1,int nums1Start,int nums1End,int[] nums2,int nums2Start,int nums2End,int k){ int nums1Len = nums1End - nums1Start + 1; int nums2Len = nums2End - nums2Start + 1; if(nums1Len ==0) return nums2[nums2Start+k]; if(nums2Len ==0) return nums1[nums1Start+k]; if(k==0) return nums1[nums1Start]<nums2[nums2Start] ? nums1[nums1Start]:nums2[nums2Start]; int nums1Mid = nums1Len*k/(nums1Len+nums2Len); int nums2Mid = k - nums1Mid - 1 ; nums1Mid = nums1Mid + nums1Start; nums2Mid = nums2Mid + nums2Start; if(nums1[nums1Mid] > nums2[nums2Mid]){ k = k - (nums2Mid - nums2Start + 1); nums1End = nums1Mid; nums2Start = nums2Mid + 1; }else if(nums1[nums1Mid] < nums2[nums2Mid]){ k = k - (nums1Mid - nums1Start + 1); nums2End = nums2Mid; nums1Start = nums1Mid + 1; }else return nums1[nums1Mid]; return findKth(nums1,nums1Start,nums1End,nums2,nums2Start,nums2End,k); } }
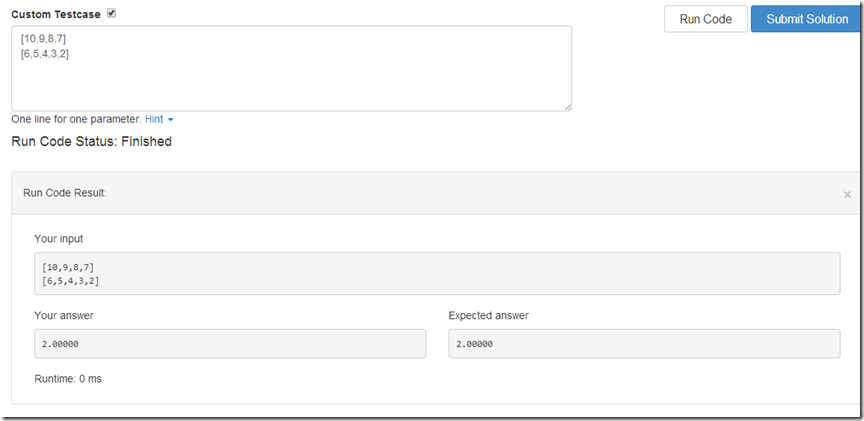
对于降序的情况:
当是降序的时候,出来这个结果:
在网上找个C++程序,当是降序的时候,上面的输入也是2.0000,上面给的期望答案也是2.0000
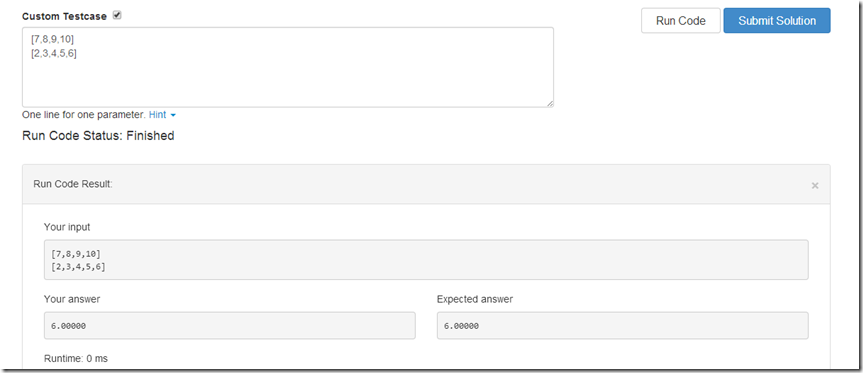
然后我就试试这个输入
上面的C++程序和上面的Java程序都是输入6.0000
题目中没有说升序的啊,但是许多人都默认升序做了,降序输入结果就不对了。
上面的Java程序和上面C++程序原理是很类似的,但是只能对升序求解,降序数组下标需要修改,大于和小于 和上面的恰好相反
好吧,咱就当升序的数组处理。上面的都对。
既然是升序,尝试用两个变量指向两个数组的开始位置,比较大小,异步前进,发现,,,,,,,,,,,,,,,,坑太大,检测中间点的可能太多,,,,,或者定义许多boolean变量检测 ,,,,,,,,,,,不写了,,是写的不对。。。已乱。。。
又转换成Python代码:
class Solution(object): def findMedianSortedArrays(self, nums1, nums2): """ :type nums1: List[int] :type nums2: List[int] :rtype: float """ nums1Len = len(nums1) nums2Len = len(nums2) if (nums1Len + nums2Len)%2==1: return 1.0*self.findKth(nums1,0,nums1Len-1,nums2,0,nums2Len-1,(nums1Len + nums2Len)/2) return (self.findKth(nums1,0,nums1Len-1,nums2,0,nums2Len-1,(nums1Len + nums2Len)/2)+self.findKth(nums1,0,nums1Len-1,nums2,0,nums2Len-1,(nums1Len + nums2Len)/2-1))*0.5 def findKth(self,nums1,nums1Start,nums1End ,nums2,nums2Start,nums2End,k): nums1Len = nums1End - nums1Start + 1 nums2Len = nums2End - nums2Start + 1 if nums1Len==0 : return nums2[nums2Start + k] if nums2Len==0 : return nums1[nums1Start + k] if k==0: return min(nums1[nums1Start],nums2[nums2Start]) nums1Mid = nums1Len*k/(nums1Len + nums2Len) nums2Mid = k - nums1Mid - 1 nums1Mid += nums1Start nums2Mid += nums2Start if nums1[nums1Mid]== nums2[nums2Mid]: return nums2[nums2Mid] if nums1[nums1Mid] > nums2[nums2Mid]: k = k - (nums2Mid - nums2Start + 1) nums1End = nums1Mid nums2Start = nums2Mid + 1 if nums1[nums1Mid] < nums2[nums2Mid]: k = k - (nums1Mid - nums1Start + 1) nums2End = nums2Mid nums1Start = nums1Mid + 1 return self.findKth(nums1,nums1Start,nums1End,nums2,nums2Start,nums2End,k)