内排序之希尔排序

内排序之希尔排序

希尔排序是直接插入排序的优化算法，维基百科上的一段话:

假设有一个很小的数据在一个已按升序排好序的数组的末端， 如果用复杂度为O(n²)的排序(冒泡排序或插入排序)， 可能会进行n次的比较和交换才能将该数据移至正确位置。而希尔排序会用较大的步长移动数据，所以小数据只需进行少数比较和交换即可到正确位置.

生命一个长度为16的数组： [13, 14, 94, 33, 82, 25, 59, 94, 65, 23, 45, 27, 73, 25, 39, 10]， 以步长为5分组，借用维基百科上的图片如下：

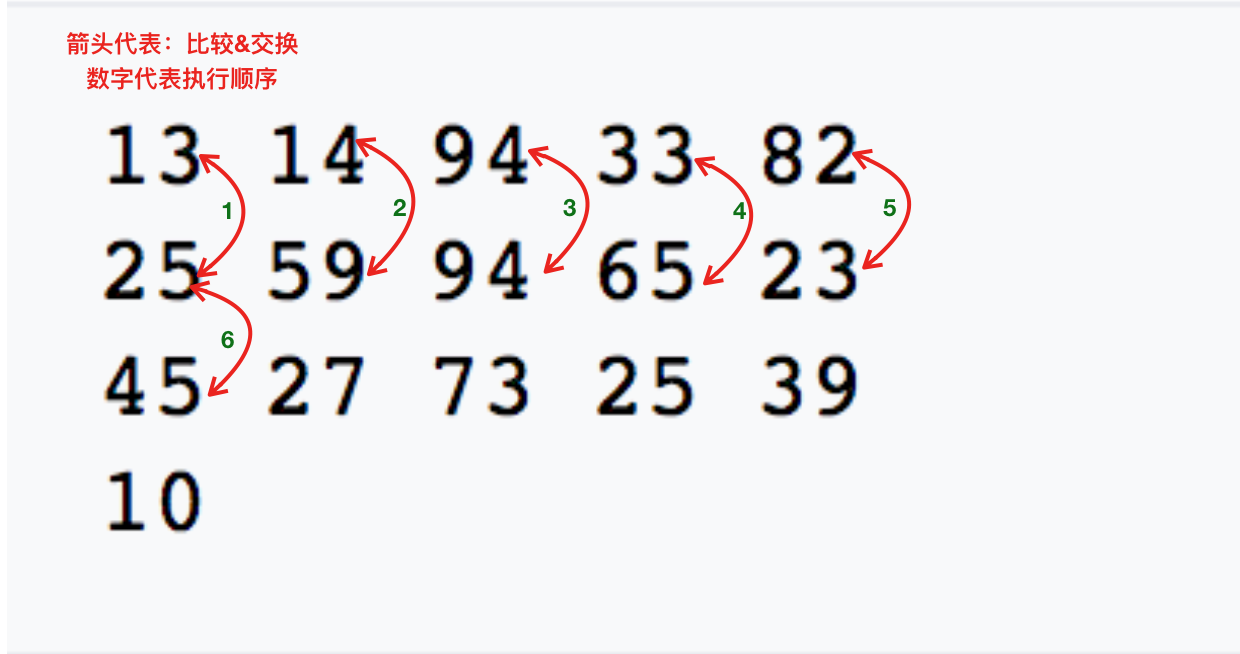
依次按列进行插入排序，例如： 对13, 25, 45, 10进行插入排序，对14, 59, 27进行插入排序...
道理是这么个道理，编码的时候，我们的递归顺序跟不是像上面说的，而是(13, 25), (14, 59)...(82, 23) 这样一排一排 横着走的，不是真的按列进行编码。
python实现的代码如下：

# coding: utf-8

def shell_sort(list):
    # 挖坑法
    n = len(list)
    # 初始步长
    gap = n // 2
    while gap > 0:
        for i in range(gap, n):
            # 每个步长进行插入排序
            temp = list[i]
            j = i
            # 插入排序
            while j >= gap and list[j - gap] > temp:
                list[j] = list[j - gap]
                j -= gap
            list[j] = temp
        # 得到新的步长
        gap = gap // 2
    return list

def shell_sort_1(list):
    # 交换法
    n = len(list)
    # 初始步长
    gap = n // 2
    while gap > 0:
        for i in range(gap, n):
            # 每个步长进行插入排序
            temp = list[i]
            # 插入排序
            j = i - gap
            while j >= 0 and temp < list[j]:
                list[j], list[j + gap] = list[j + gap], list[j]
                j -= gap
        # 得到新的步长
        gap = gap // 2
    return list


if __name__ == "__main__":
    a = [3, 1, 9, 2, 3, 11, 8, 2, 0]
    print(a)
    shell_sort_1(a)
    # shell_sort(a)
    print(a)