信息的表示和处理之浮点数

浮点数

浮点表示对形如的有理数进行编码。它对执行涉及非常大的数字、非常接近于的数字，以及更普遍地作为实数运算的近似值的计算，是很有用的。

二进制小数

理解浮点数的第一步是考虑含有小数值的二进制数字。首先，让我们来看看更熟悉的十进制表示法。十进制表示法使用如下形式的表示：

其中每个十进制数d_i的取值范围是0~9。这个表达描述的数值d定义如下：

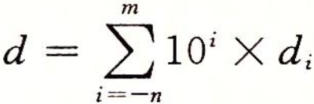
数值权的定义与十进制小数点符号（‘.’）相关，这意味着小数点的左边的数字的权是10的正幂，得到整数值，右边数字的权是10的负幂，得到小数值。例如，12.34₁₀表示数字

类似，考虑一个形如的表示法，其中每个二进制数字，或者称为位，bi的取值范围是0和1，如图2-26所示。这种表示方法表示的数b定义如下：

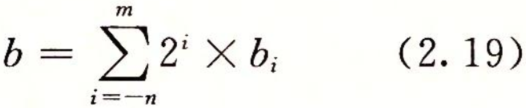
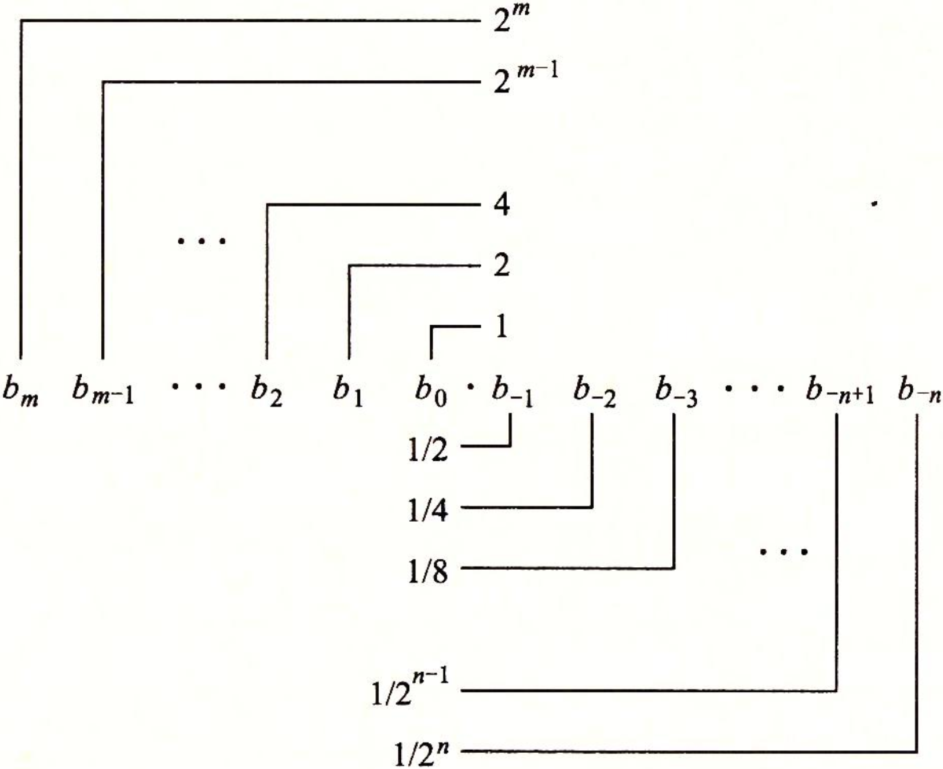
图2-26   小数的二进制表示。二进制点左边的数字的权形如2ⁱ，而右边额数字的权形如1/2ⁱ

符号‘.’现在变为二进制的点，点左边的位的权是2的正幂，点右边的位的权是2的负幂。例如，101.11₂表示数字。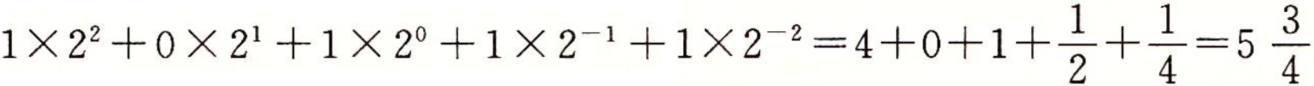

从等式（2.19）中可以很容易看出，二进制小数点向左移动一位相当于这个数被2除。例如，101.11₂表示数，而10.111₂表示数。类似，二进制数小数点向右移动一位相当于该数乘2。例如1011.1₂表示数。

注意，形如0.11……1₂的数表示的数是刚好小于1的数。例如，0.111111₂表示，我们将用简单的表示法来表示这样的数值。

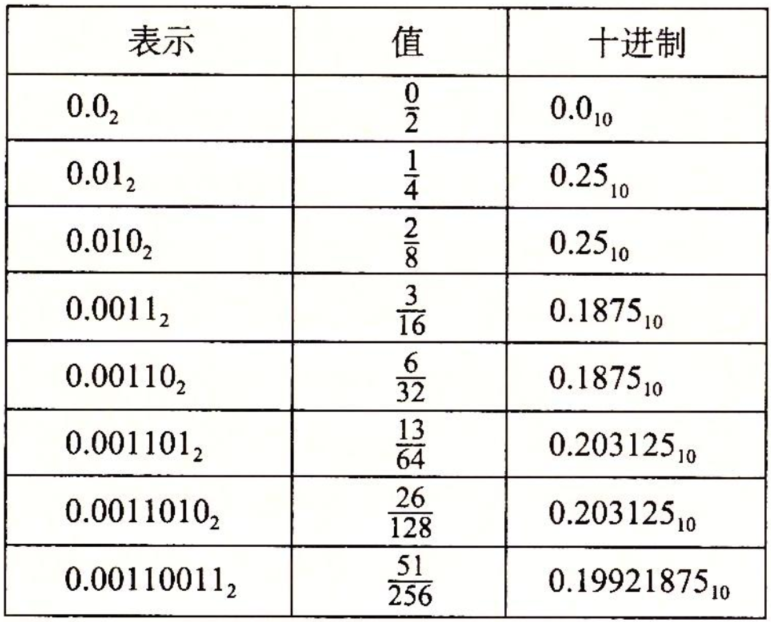
假定我们仅考虑有限长度的编码，那么十进制表示法不能准确地表达像1/3和5/7这样的数。类似，小数的二进制表示法只能表示能够被写成的数。其他的值只能够被近似的表示。例如，数字1/5可以用十进制小数0.20精确表示。不过，我们并不能把它准确地表示为一个二进制小数，我们只能近似地表示它，增加二进制表示的长度可以提高表示精度：

IEEE浮点表示

前面提到，定点表示法不能很有效地表示非常大的数字。例如，表达式5*2¹⁰⁰是用101后面跟随100个零的位模式来表示。相反，我们希望通过给定x和y的值，来表示形如的数。

IEEE浮点标准用的形式来表示一个数：

• 符号（sign）s决定是负数（s=1）还是正数（s=0），而对于数值0的符号位解释作为特殊情况处理。
• 尾数（significand）M是一个二进制小数，它的范围是1~2-ε，或者是0~1-ε。
• 阶码（exponent）E的作用是对浮点数加权，这个权重是2的E次幂（可能是负数）。

将浮点数的位表示划分为三个阶段，分别对这些值进行编码：

• 一个单独的符号位s直接编码符号s。
• k位的阶码字段exp=e_k-1……e₁e₀编码阶码E。
• n位小数字段frac=f_n-1……f₁f₀编码尾数M，但是编码出来的值也依赖于阶码字段的值是否等于0。

图2-27给出了将这三个字段装进字中两种最常见的格式。在单精度浮点格式（C语言中的float）中，s、exp和frac字段分别为1位、k=8位和n=23位，得到一个32位的表示。在双精度浮点格式（C语言的double）中，s、exp和frac字段分别为1位、k=11位和n=52位，得到一个64位的表示。

图2-27   标准浮点格式（浮点数由3个字段表示。两种最常见的格式是它们被封装到32位（单精度）和64位（双精度）的字中）

给定位表示，根据exp的值，被编码的值可以分成三种不同的情况（最后一种情况有两个变种）。图2-28说明了对单精度格式的情况。

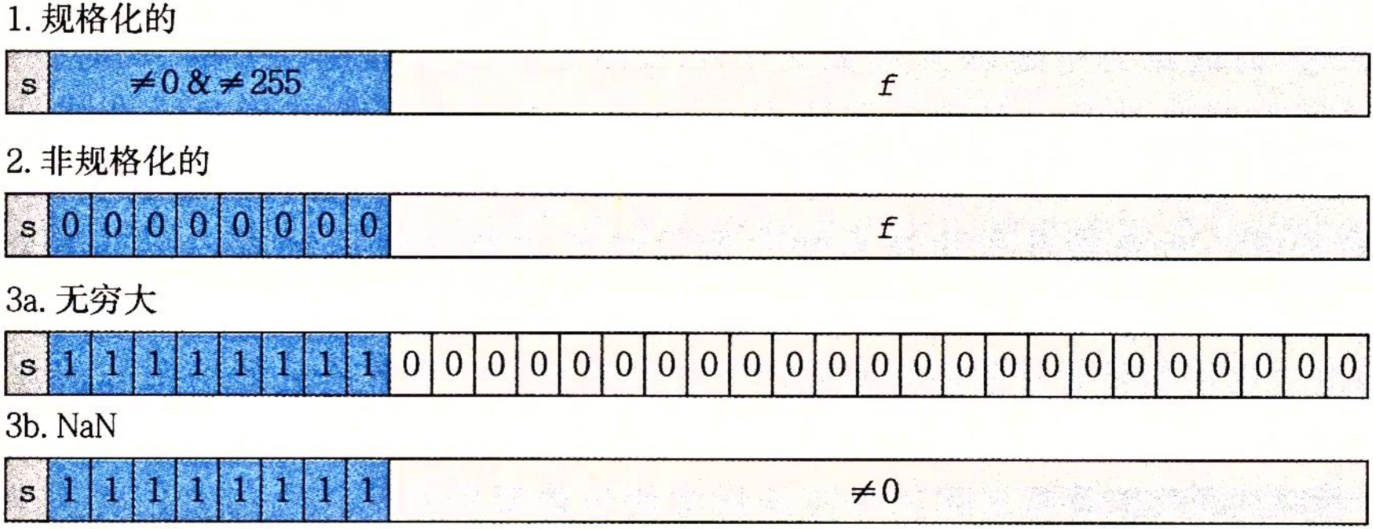
图2-28   单精度浮点数值的分类（阶码的值决定了这个数时规格化的、非规格化的或特殊值）

情况1：规格化的值

这是最普遍的情况。当exp的位模式既不全是0，也不全是1（单精度数值为255，双精度数值为2047）时，都属于这类情况。在这种情况中，阶码字段被解释为以偏置（biased）形式表示的有符号整数。也就是说，阶码的值是E=e-Bias，其中e是无符号数，其位表示为e_k-1……e₁e₀，而Bias是一个等于2^k-1-1（单精度是127，双精度是1023）的偏置值。由此产生指数的取值范围，对于单精度是-126~+127，而对于双精度是-1022~+1023。

小数字段frac被解释为描述小数值f，其中0<=f<1，其二进制表示为0.f_n-1……f₁f₀，也就是二进制小数点在最高有效位的左边。尾数定义为M=1+f。有时，这种方式也叫做隐含的以1开头的表示，因为我们可以把M看成一个二进制表达式1.f_n-1f_n-2……f₀的数字。既然我们总是能调整阶码E，使得尾数M在范围1<=M<2之中（假设没有溢出），那么这种表示方法是一种轻松获得一个额外精度位的技巧。既然第一位总是等于1，那么我们就不需要显示地表示它。

情况2：非格式化的值

当阶码域全为0时，所表示的数是非规格化形式。在这种情况下，阶码值是E=1-Bias，而尾数的值是M=f，也就是小数字段的值，不包含隐含的开头1。

非规格化数有两个用途。首先，它们提供了一种表示数值0的方法，因为使用规格化数，我们必须总是使M>=1，因此我们就不能表示0。实际上，+0.0的浮点表示的位模式为全0：符号位全为0，阶码字段全是0，而小数域也全为0，这就得到M=f=0。令人奇怪的是，当符号位为1，而其他域全为0时，我们得到值-0.0。根据IEEE的浮点格式，值+0.0和-0.0在某些方面被认为是不同的，而在某些方面又是相同的。

情况3：特殊值

最后一类数值是当阶码全为1的时候出现的。当小数域全为0时，得到的值表示负无穷，当s=0时是+∞，或者当s=1时是-∞。当我们把两个非常大的数相乘，或者除以0时，无穷能够表示溢出的结果。当小数域为非零时，结果值被称为“NaN”，即“不是一个数（Not a Number）”的缩写。一些运算结果不能是实数或者无穷，就会返回NaN值，比如当计算或时。在某些应用中，表示未初始化的数据时，它们也很有用处。

数字示例

图2-29展示了一组数值，它们假定可以用6位格式来表示，有k=3的阶码位和n=2的尾数位。偏置量是2^3-1-1=3。图中的a部分显示了所有可表示的值（除了NaN）。两个无穷值在两个末端。最大数量值的规格化数是±14。非规格化数聚集在0的附近。图的b部分中，我们只展示了介于-1.0和+1.0之间的数值，这样就能够看的更加清楚了。两个零是特殊的非规格化数。可以观察到，那些可表示的数并不是均匀分布的，越靠近原点它们越稠密。

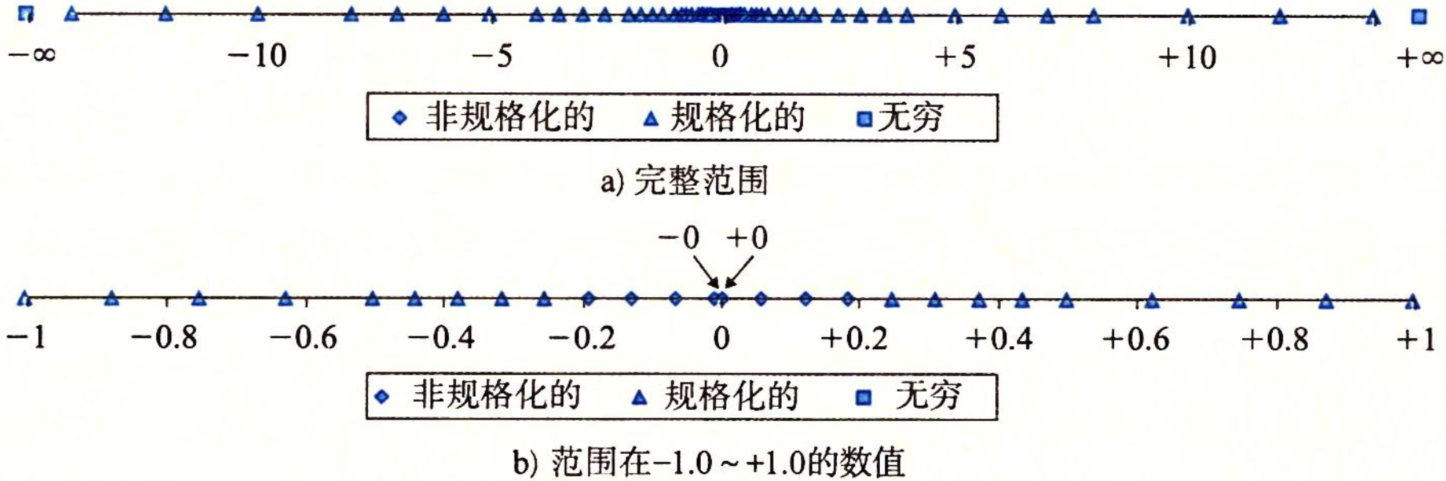
图2-29   6位浮点格式可表示的值（k=3的阶码位和n=2的尾数位。偏置量是3）

图2-30展示了假定的8位浮点格式的示例，其中有k=4的阶码位和n=3的小数位。偏置量是2^4-1-1=7。图被分成了三个区域，来描述三类数字。不同的列给出了阶码字段是如何编码阶码E的，小数字段是如何编码尾数M的，以及它们在一起是如何形成要表示的值。从0自身开始，最靠近0的是非规格化数。这种格式的非规格化数的E=1-7=-6，得到的权2^E=1/64。小数f的值的范围是0,1/8,……,7/8，从而得到数字V的范围是。

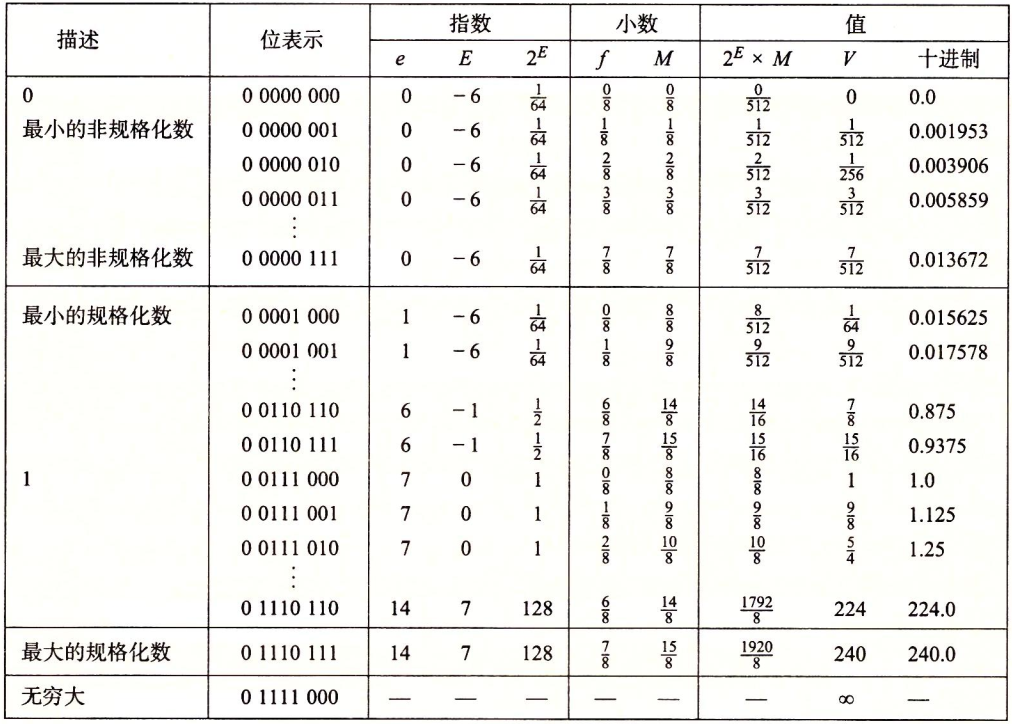
图2-30   8位浮点格式的非负值示例（k=4的阶码位和n=3的小数位。偏置量是7）

这种形式的最小规格化数同样有E=1-7=-6，并且小数取值范围也为0,1/8,……,7/8。然而，尾数在范围1+0=1和1+7/8=15/8之间。得出数V在范围8/512=1/64和15/512之间。

可以观察到最大非规格化数7/512和最小规格化数8/512之间的平滑转变。这种平滑性归功于我们对非规格化数的E的定义。通过将E定义为1-Bias，而不是-Bias，我们可以补偿非规格化数的尾数没有隐含的开头1。

当增大阶码时，我们成功地得到更大的规格化值，通过1.0后得到最大的规格化数。这个数具有阶码E=7，得到一个权2^E=128。小数等于7/8得到尾数M=15/8。因此，数值是V=240.0。超出这个值就会溢出到+∞。

图2-31展示了一些重要的单精度和双精度浮点数的表示和数字值。根据图2-30中展示的8位格式，我们能够看出有k位阶码和n位小数的浮点表示的一般属性。

图2-31   非负浮点数的示例

• 值+0.0总有一个全为0的位表示。
• 最小的正非规格化值的位表示，是由最低有效位为1而其他位为0构成的。它具有小数（和尾数）值M=f=2^-n和阶码值E=-2^k-1+2。因此它的数字值是。
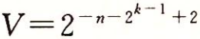• 最大的非规格化值的位模式是由全为0的阶码字段和全为1的小数字段组成。它有小数（和尾数）值M=f=1-2^-n（我们写成1-ε）和阶码值E=-2^k-1+2。因此数值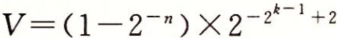，这仅比最小的规格化值小一点。
• 最小的正规格化值的位模式的阶码字段的最低有效位为1，其他位全为0。它的尾数值M=1，而阶码值E=-2^k-1+2。因此，数值。

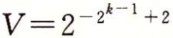• 值1.0的位表示额阶码字段除了最高有效位等于1以外，其他位都等于0。它的尾数值是M=1，而它的阶码值是E=0。

•  最大的规格化值的位表示的符号位为0，阶码的最低有效位等于0，其他位等于1。 它的小数值f=1-2^-n，尾数M=2-2^-n（我们写作2-ε），它的阶码值E=2k-1-1，得到数值。

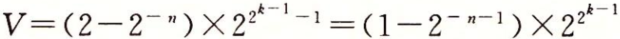我们知道12345具有的二进制表示[11000000111001]，通过将二进制小数点左移13位，我们创建这个数的规格化表示，得到12345=1.1000000111001₂*2¹³。为了用IEEE单精度形式来编码，我们丢弃开头的1，并在末尾增加10个0，来构造小数字段，得到二进制表示[10000001110010000000000]。为了构造阶码字段，我们用13加上偏置量127，得到140，其二进制表示[10001100]。加上符号位0，我们就得到二进制的浮点表示[01000110010000001110010000000000]。我们观察到整数值12345（0x3039）和单精度浮点数值12345.0（0x4640E400）再在位级表示上有下列关系：

舍入

因为表示方法限制了浮点数的范围和精度，所以浮点运算只能近似地表示实数运算。因此，对于x，我们一般想用一种系统的方法，能找到‘最接近的’匹配值x'，它可以用期望的浮点形式表示出来。这就是舍入运算的任务。一个关键的问题是舍入方向，如1.5是应该舍入为1还是2呢？一种可选择的方法是维持实际数字的下界和上届。例如，我们可以确定可表示的值x^-和x⁺，使得x的值位于它们之间：x^-<=x<=x⁺。IEEE浮点格式定义了四种不同的舍入方式。默认的方法是找到最接近的匹配，而其他三种可用于计算上界和下界。图2-32举例说明了四种舍入方式，将一个浮点数舍入到最接近额整数。

图2-32   以浮点数舍入为例说明舍入方式

其他三种方式产生实际值得确界。这些方法在一些数字应用中是很有用的。向零舍入方式把正数向下舍入，把负数向上舍入，得到，使得。向下舍入方式把正数和负数都向下舍入，得到值x^-，使得x^-<=x。向上舍入方式把正数和负数都向上舍入，得到值x⁺，满足x<=x⁺。

向偶数舍入：有效数字超出规定数位的多余数字是1001，它大于超出规定最低位的一半（即0.5），故最低位进1。如果多余数字是0111，它小于最低位的一半，则舍掉多余数字（截断尾数、截尾）即可。对于多余数字是1000、正好是最低位一半的特殊情况，最低位为0则舍掉多余位，最低位为1则进位1、使得最低位仍为0（偶数）。

浮点运算

IEEE标准指定了一个简单的规则，来确定诸如加法和乘法这样的算数运算结果。把浮点值x和y看成实数，而某个运算⊙定义在实数上，计算将产生Round(x⊙y)，这是对实际运算的精确结果进行舍入后的结果。在实际中，浮点单元的设计者使用一些小技巧来避免这种精确计算，因为计算只要精确到能够保证得到一个正确的舍入结果就可以了。当参数中有一个是特殊值（如-0、-∞、或NaN）时，IEEE标准定义了一些使之更合理的规则。例如，定义1/-0将产生-∞，而定义1/+0会产生+∞。

我们将定义为Round(x+y)。这个运算的定义针对x和y的所有取值，虽然x和y都是实数，由于溢出，该运算可能得到无穷值。对于所有x和y的值，这个运算是可交换的，也就是说。另一方面，这个运算是不可结合的。例如，使用单精度浮点，表达式(3.14 + 1e10)-1e10得出值3.139999——因为舍入，精度丢失。另一方面3.14+(1e10-1e10)得出值3.14。大多数值在浮点加法下都有逆元，也就是说。无穷（因为+∞-∞=NaN）和NaN是例外情况，因为对于任何x，都有。

浮点加法不具有结合性，这是缺少的最重要的群属性。对于科学计算程序员和编译器编写者来说，这具有重要的意义。例如，假设一个编译器给定了如下代码片段：

x=a+b+c
y=b+c+d

　　

编译器可能试图通过产生下列代码来省去一个浮点加法：

t=b+c
x=a+t
y=t+d

　　

另一方面，浮点加法满足了单调性属性：如果a>=b，那么对于任何a、b以及x的值，除了NaN，都有x+a>=x+b。无符号或补码加法不具有这个实数（和整数）加法的属性。

浮点乘法也遵循通常乘法所具有的许多属性。我们定义为Round(x*y)。这个运算在乘法中是封闭的（可能产生无穷大或NaN），它是可交换的，而且它的乘法单元为1.0。另一方面，由于可能发生溢出，或者由于舍入而失去精度，它不具有可结合性。例如，单精度浮点情况下，表达式(1e20*1e20)*1e-20求值为+∞，而1e20*(1e20*1e-20)将得到1e20。另外，浮点乘法在加法行不具备分配性。例如，单精度浮点情况下，表达式1e20*(1e20-1e20)求值为0.0，而1e20*1e20-1e20*1e20会得到NaN。

另一方面，对于任何a、b和c，且都不为NaN，浮点乘法满足下列单调性：

此外，我们还可以保证，只要a!=NaN，就有。就像我们先前所看到的，无符号或补码的乘法没有这些单调性属性。

C语言中的浮点数

所有的C语言版本提供了两种不同的浮点数据类型：float和double。在支持IEEE浮点格式的机器上，这些数据类型就对应于单精度和双精度浮点。另外，这些浮点数使用向偶数舍入的舍入方式。不幸的是，因为C语言标准不要求机器使用IEEE浮点，所以没有标准的方法来改变舍入方式或得到诸如-0、+∞、-∞或者NaN之类的特殊值。大多数系统提供include('.h')文件和读取这些特征的过程库，但是细节随系统不同而不同。例如，当程序文件中出现下列代码时，GNU编译器GCC会定义程序常数INFINTTY(+∞)和NAN(表示NaN)：

#define _GNU_SOURCE 1
#include <math.h>

　　

当int、float和double格式之间进行强制类型转换时，程序改变数值和位模式的原则如下（假设int是32位）：

• 从int转换成float，数字不会溢出，但是可能被舍入。
• 从int或float转换成double，因为double有更大的范围，也有更高的精度，所以能够保留精确的数值。
• 由double转换成float，因为范围要小一些，所以值可能溢出成+∞或-∞。另外，由于精确度较小，它还可能被舍入。
• 从float或double转换成int，值将向零舍入。如1.999将被转换成1，而-1.999将被转换成-1。进一步来说，值可能会溢出。C语言标准没有对这种情况指定固定的结果。与Intel兼容的微处理器指定位模式[10……00]（字长为w时的TMin_w）为整数不确定值。一个从浮点数到整数的转换，如果不能为该浮点数找到一个合理的整数近似值，就会产生这样一个值。因此，表达式(int)+1e10会得到-21483648，即从一个正值变成一个负值。